Системы ОДУ
Многие физические процессы описываются с помощью нескольких ОДУ, то есть в виде системы, которую в общем виде принято записывать так: 
(1). В системе 1 неизвестными являются 
, где x- независимая переменная.
Определение 1
Порядком системы ОДУ называется число 
Определение 2
Совокупность соотношений вида { 
(2), где x- независимая переменная, называется системой дифференциальных уравнений первого порядка.
Определение 3
Система дифференциальных уравнений первого порядка 2, разрешённая относительно производных, называется нормальной системой ОДУ и имеет вид 3.
{ 
(3)
Определение 4
Если в системе 3 функции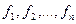 
явно не зависят от x, то данная системаскольких ОДУ, то есть в виде системы, которую в общем виде принято записывть так:... ОДУ называется стационарной или автономной.
Задача Коши
При решении конкретной физической задачи приходится иметь дело с понятием математической модели, которая включает в себя систему ОДУ вида 1 или 2 и граничные условия. Так для нормальной системы ОДУ 3 начальные условия задаются в некоторой точке интервала, например в точке 
, и записывается так: 
(4) здесь 
– заданные числа, которые называются начальными условиями. Системы ОДУ 3 и 4 называются математической моделью, в результате решения которой получают частное решение. Прежде чем находить решение математической модели 3-4, необходимо проверить её на существование и единственность решения.
Теорема Коши
Если в некоторой области G n+1- мерного пространства переменных 
в системе 3 в точке функции 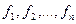являются непрерывными по своим аргументам и имеют непрерывные частные производные 
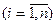. В исходной точке и её окрестности, то решение данной математической модели 3-4 существует и оно единственно и имеет вид 
Замечание
Если условия теоремы выполняются в любой точке области G, то решение математической модели 3-4 существует единственно во всей области G.
Определение 5
Точка (). n+1 – мерного пространства называется обыкновенной для системы 2, если эта система имеет единственное решение и удовлетворяет начальному условию 4.
Определение 6
Пусть любая точка 
n+1-мерного пространства области G является обыкновенной, тогда можно найти функции { 
(5), где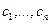 
– некоторые постоянные, удовлетворяющие системе 2, называются общим решением этой системы.
Замечание
Если потребовать, чтобы общее решение 5 удовлетворяло начальным условиям 4, то мы определим значения постоянных 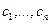и тем самым получим частное решение.
Некоторые методы решения систем ОДУ
В дальнейшем будем рассматривать методы решения, как задачи Коши для нормальной системы ОДУ, так и для получения общего решения нормальной системы ОДУ.
