РГЗ-1 (1 часть). Определить расстояние от точки до плоскости.

Р а б о ч а я

Тетрадь

АКСИОМЫ ГЕОМЕТРИИ и некоторые СЛЕДСТВИЯ ИЗ НИХ

Перед изучением начертательной геометрии необходимо основательно повторить начальный курс геометрии, уделив особое внимание разделам описания свойств простых фигур и методам решения геометрических задач на построения.

Основные свойства принадлежности точек и прямых

Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну.

Основные свойства взаимного расположения точки на прямой и на плоскости

Из трех точек на прямой одна и только одна лежит между двумя другими.

Через 3 точки, не лежащие на одной прямой, можно провести только одну плоскость.

Прямая разбивает плоскость на две полуплоскости.

Через прямую и не лежащую на ней точку можно провести плоскость, и только одну.

Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

Основные свойства параллельных прямых и плоскостей

Через точку, не лежащую на данной прямой, можно провести только одну параллельную прямую.

Через точку вне данной плоскости можно провести плоскость, параллельную данной, и только одну.

Если прямая, не принадлежит плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.

Плоскости параллельны, если каждая параллельна пересекающимся прямым, лежащим в другой плоскости.

Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.

Угол между скрещивающимися прямыми - угол между пересекающимися параллельными им прямыми.

Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проходящими через эти прямые.

Расстояние от прямой до параллельной ей плоскости - расстояние от любой ее точки до этой плоскости.

Основные свойства плоскостей в пространстве

Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и не принадлежащие ей.

Если две различные плоскости имеют общие точки, то они пересекаются по прямой.

Если две прямые имеют общую точку (пересечения), то они описывают плоскость, и притом только одну.

Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.

Перпендикулярность прямых и плоскостей

Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, то она перпендикулярна плоскости.

Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.

Две прямые, перпендикулярные одной и той же плоскости, параллельны.

Если плоскость проходит через перпендикуляр к другой плоскости, то эти плоскости перпендикулярны.

Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна их линии пересечения, то она перпендикулярна и другой плоскости (линии связи).

Основные свойства измерения отрезков и углов

Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180^o. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Основные свойства откладывания отрезков и углов

На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 градусов, и только один.

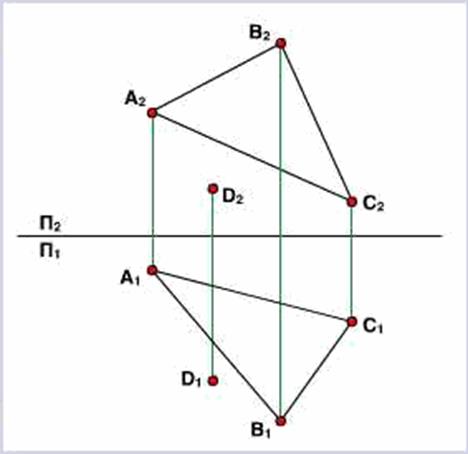
Задана точка А (15, 20, 30).

Построить проекции точек, симметричных точке А:

В – относительно плоскости П1, С –относительно плоскости П2,

D – относительно оси проекций ox, Е – относительно начала координат.

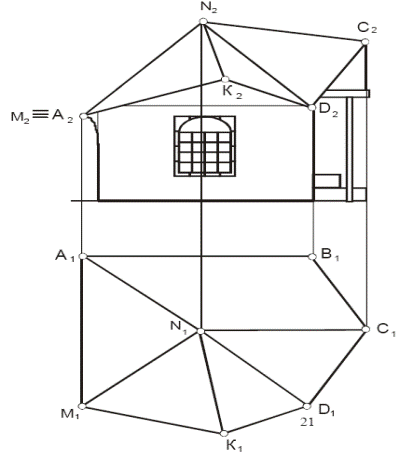
Построить эпюр пирамиды.

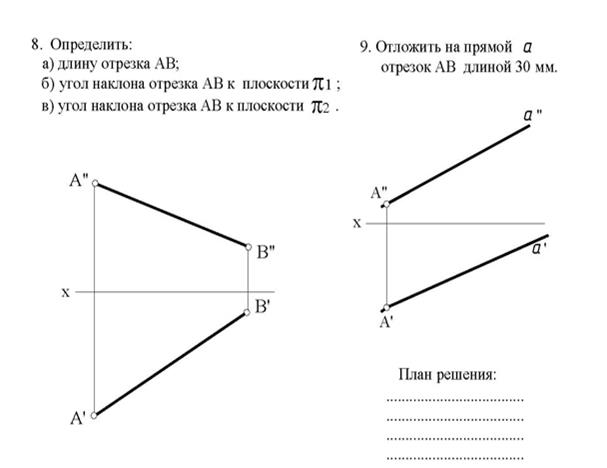
Задание №1. ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА и УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ.
	Длину отрезка АВ можно определить из прямоугольного треугольника .

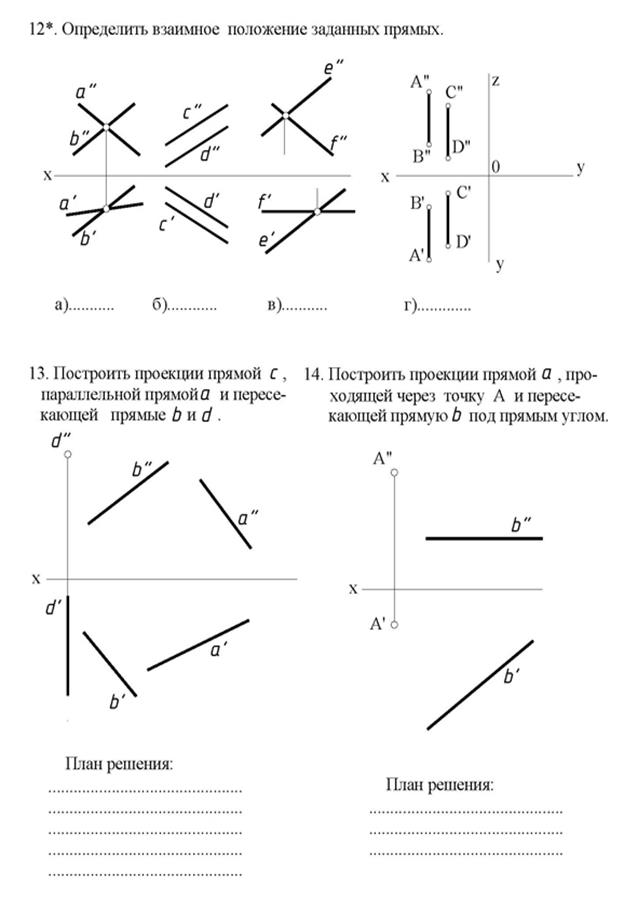
Задание 2. Построить ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ пересекающиеся ЛИНИИ
	Теорема 1. Для того чтобы прямой угол проецировался в истинную величину, необходимо и достаточно, чтобы одна из его сторон была параллeльна, а другая не перпендикулярна плоскости проекций.

Задание 3. Постройте СЛЕДЫ ПРЯМОЙ ЛИНИИ (прямая задача).

ответить: через какие октанты проходить линия 12?

Задание 4. Построить линию по ее следам (обратная задача).

	A (x, y, z)	B (x, y, z)

След

ответить: через какие октанты проходить линия?

Теорема 1 (стр. 8).

В чем отличие горизонтальной линии от горизонтали?

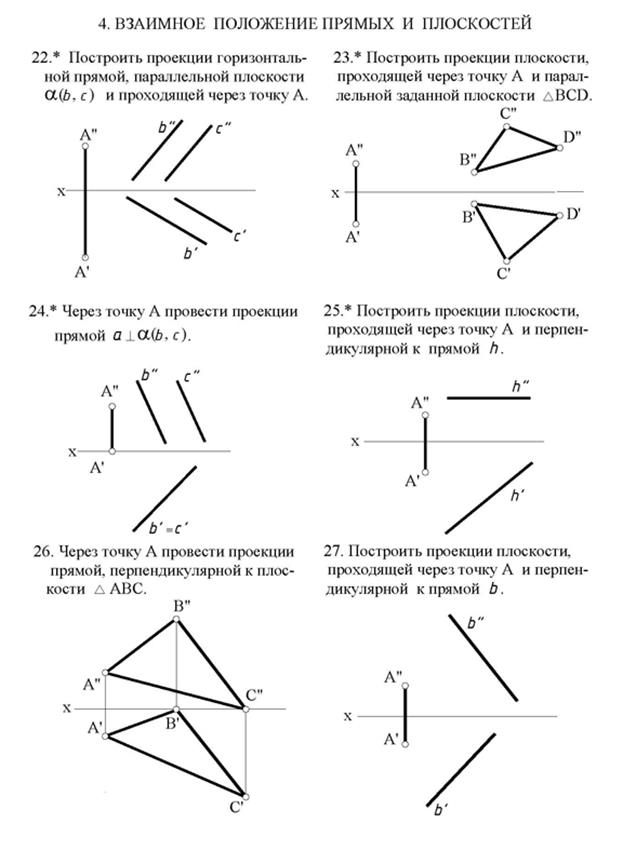
Построить направление потоков дождя на крыше здания. Определить линии ската элементов крыши. Линия наибольшего наклона плоскости к плоскости Н перпендикулярна горизонталям, а ЛНН к плоскости V перпендикулярна фронталям этой плоскости.

Чтобы на эпюре построить плоскость (α), перпендикулярную данной (β), не-

обходимо, чтобы одна из них проходила через перпендикуляр к другой.

Задание 5.
Задание 6. Плоскость. Прямая и точка в плоскости.

В плоскости ската крыши АВСD размечен четырехугольник для слухового окна KLMN. Построить его недостающую проекцию.

С помощью линий уровня построить горизонтальную проекцию ΔАВС, принадлежащего плоскости β(m∩ℓ). Определить угол наклона плоскости к плоскости Н.

Теорема 2. Если прямая перпендикулярна к плоскости в пространстве, то на комплексном чертеже горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция перпендикулярна к фронтальной проекции фронтали, принадлежащим этой плоскости.

Задание 7.

Определить точку пересечения прямой ЕF с плоскостью β.

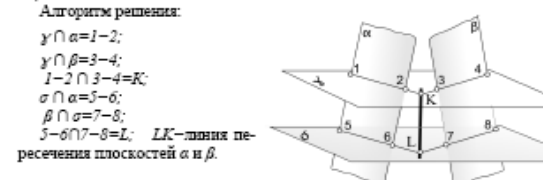
Порядок решения задачи (алгоритм решения):

1. Провести через данную прямую вспомогательную плоскость (удобнее проецирующую);

2. Построить линию пересечения данной и вспомогательной плоскостей 1−2=β∩α;

3. Отметить искомую точку на пересечении данной прямой с линией пересечения плоскостей К=(1-2) ∩EF ⇒ K=EF∩β.

РГЗ-1 (1 часть). Определить расстояние от точки до плоскости.