Действительные числа. Множества. Практика

Множества

Задание 1. Ответить на вопросы теста

Тест 1

Вопрос 1Множество, не содержащее ни одного элемента, называется
а.) пустым	б.) неопределённым	в.) универсальным	г.) подмножеством
Вопрос 2Если каждый элемент множества А является элементом множества В, то
а.) В Ì А	б.) В É А	в.) А Ì В	г.) А É В
Вопрос 3Если А Ì В и В Ì А, то
а.) А - подмножество множества В	б.) В - подмножество множества А	в.) А = В	г.) А и В - совпадают
Вопрос 4Множество, состоящее из элементов, каждый из которых принадлежит, хотя бы одному из множеств А или В называется
а.) пересечением	б.) объединением	в.) произведением	г.) суммой
Вопрос 5Множество, состоящее из элементов, каждый из которых принадлежит, обоим множествам и А и В называется
а.) пересечением	б.) объединением	в.) произведением	г.) суммой
Вопрос 6Выбрать множество, являющееся подмножеством натуральных чисел
а.) {-2; 4; 6; 10}	б.) {0; 4; 6; 10}	в.) {2; 4; 6; 7,8}	г.) {2; 4; 6; 10}
Вопрос 7Выбрать множество, являющееся подмножеством целых чисел
а.) {-2; 4; 6; 10}	б.) {-2; 0; 6; Ö8}	в.) {0; 4; 6; 9,5}	г.) {-2; 0; 6; p}
Вопрос 8Выбрать множество, являющееся подмножеством рациональных чисел
а.) {-2; 0; 6; ln 2}	б.) {-2; 0; 1; p }	в.) {-2; 0; 6/7; Ö9}	г.) {-2/3; 0; 6; Ö8}
Вопрос 9Числовой промежуток вида [2; 6] – это
а.) отрезок	б.) сегмент	в.) замкнутый промежуток	г.) интервал
Вопрос 10Числовой промежуток вида (-2; 1) – это
а.) интервал	б.) полуинтервал	в.) открытый промежуток	г.) сегмент
Вопрос 11Числовой промежуток вида (-3; 5] – это
а.) полуоткрытый интервал	б.) отрезок	в.) луч	г.) полуоткрытый отрезок
Вопрос 12Выберите конечные интервалы
а.) (-¥; 1)	б.) (-3; 5]	в.) (-¥; 1]	г.) (-2; 1)
Вопрос 13Выберите бесконечные интервалы
а.) (-2; 1)	б.) [2; 5]	в.) (-¥; +¥)	г.) [-2; ¥)
Вопрос 14Окрестностью точки х 0=4 не является
а.) (4; 6)	б.) (-5; 3)	в.) (0; 8)	г.) [4; 7]
Вопрос 15Окрестностью точки х 0=-3 является
а.) (-3; 0)	б.) (-5; -3]	в.) (-5; 2)	г.) (1; 5)
Вопрос 16 e -окрестностью точки х 0=3 является
а.) (1; 5)	б.) (2; 6)	в.) [1; 5)	г.) [1; 5]
Вопрос 17У e -окрестности точки х 0 вида | х -3|<2
а.) 3 – центр; 2 – радиус	б.) -3 – центр; 2 – радиус	в.) 3 – центр; -2 – радиус	г.) -3 – центр; -2 – радиус
Вопрос 18У e -окрестности точки х 0 вида | х +1|<5
а.) 1 – центр; 5 – радиус e-окрестности;	б.) 1 – центр; -5 – радиус e-окрестности;	в.) -1 – центр; 5 – радиус e-окрестности;	г.) -1 – центр; -5 – радиус e-окрестности;
Вопрос 19Пусть множество Х ={2; 4; 6; 9}. Укажите верное утверждение
а.) 6Î Х	б.) 5Î Х	в.) 2Ï Х	г.) 1Ï Х
Вопрос 20Пусть множество Х =(-3; -1]È[2; 4). Укажите верное утверждение
а.) -3Î Х	б.) 2Î Х	в.) -1Ï Х	г.) 1Ï Х

Задание 2. Из каких элементов состоит данное множество?

А ={1; 25} – данная запись означает, что множество А состоит из двух чисел 1 и 25	В ={-3; 4} – данная запись означает, что множество В состоит из
запись А ={ х: 1< x <25} – означает, что множество А состоит из всех действительных (если не оговорено) чисел, удовлетворяющих двойному неравенству 1< x <25;	запись В ={ х: 1< x <4} – означает, что множество B состоит из
запись А ={ х Î N | 1< x <25} – означает, что множество А состоит из всех натуральных чисел, удовлетворяющих двойному неравенству 1< x <25.	запись В ={ х Î Z | -3< x <4} – означает, что множество B состоит из

 

Задание 3. Произвести операции над множествами:

А ={1; 3; 5; 6}; В ={1; 2; 5; 7; 8}; U ={0; 1; 2; 3; 4; 5; 6; 7; 8; 9}: 1) А È В = В È А ={1; 2; 3; 5; 6; 7; 8}; 2) А È U = U È А = U ={0; 1; 2; 3; 4; 5; 6; 7; 8; 9}; 3) В È U = U È В = U ={0; 1; 2; 3; 4; 5; 6; 7; 8; 9}; 4) А Ç В = В Ç А ={1; 5}; 5) А Ç U = U Ç А = A= {1; 3; 5; 6}; 6) B Ç U = U Ç B = B ={1; 2; 5; 7; 8}; 7) А \ В ={1; 3; 5; 6}\{1; 2; 5; 7; 8}={3; 6}; 8) В \ А ={1; 2; 5; 7; 8}\{1; 3; 5; 6}={2; 7; 8}; 9) U \ А = U \{1; 3; 5; 6}={0; 2; 4; 7; 8; 9}; 10) А \ U =Æ; 11) U \ В = U \{1; 2; 5; 7; 8}={0; 3; 4; 6; 9}; 12) В \ U =Æ;

А ={0; 2; 4; 7; 8}; В ={1; 2; 4; 9}; U ={0; 1; 2; 3; 4; 5; 6; 7; 8; 9}: 1) А È В = 2) А È U = 3) В È U = 4) А Ç В = 5) А Ç U = 6) B Ç U = 7) А \ В = 8) В \ А = 9) U \ А = 10) А \ U = 11) U \ В = 12) В \ U =

 

Задание 4. Произвести операции над множествами:

А =(1; 5]; В =(4; 7); U = R. 1) А È В = В È А =(1; 5]È(4; 7)=(1; 7); 2) А È U = U È А = U; 3) В È U = U È В = U; 4) А Ç В = В Ç А =(1; 5]Ç(4; 7)=(4; 5]; 5) А Ç U = U Ç А = A; 6) B Ç U = U Ç B = B; 7) А \ В =(1; 5]\(4; 7)=(1; 4]; 8) В \ А =(4; 7)\(1; 5]=(5; 7); 9) U \ А = R \(1; 5]=(-¥; 1]È(5; +¥); 10) U \ В = R \(4; 7)=(-¥; 4]È[7; +¥); 11) А \ R = В \ R =Æ

А =[2; 8]; В =(4; 8); U = R. 1) А È В = 2) А È U = 3) В È U = 4) А Ç В = 5) А Ç U = 6) B Ç U = 7) А \ В = 8) В \ А = 9) U \ А = 10) U \ В = 11) А \ R =

Задание 5. Показать результат операций над множествами с помощью диаграмм Эйлера-Венна:

 

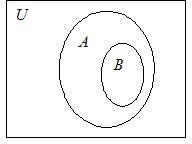
А È В	А È В	А È В
А Ç В	А Ç В	А Ç В
А \ В	А \ В	А \ В
B \ A	B \ A	B \ A
U \ A	U \ A	U \ A

U \ B	U \ B	U \ B
B D A	B D A	B D A

 

Факториал

Факториалом натурального числа n! – называется произведение всех натуральных чисел не превосходящих данного.

n!=1·2·…·(n -1)· n

Например:

5!=1·2·3·4·5=

4!=1·2·3·4=

3!=1·2·3=

2!=1·2=

1!=

0!= – единственное не натуральное число, для которого рассчитывается факториал.

Задание 6. Вычислить:

 

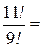
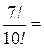
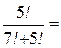
-4!=	(-4)!=	1,4!=

 

Задание 7. Найти множество решений методом интервалов:

 

1) | x +2|-| х -4|=-6;

Находим нули модулей:

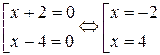
Разбиваем числовую ось данными значениями на три интервала и раскрываем знак модуля на каждом из них и получаем:

 

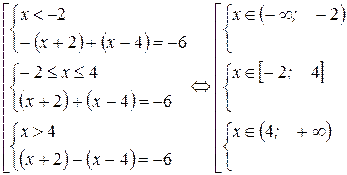
Ответ:

 

2) | x +2|-| х -4|=2 х -4;

Находим нули модулей:

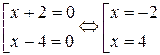
Разбиваем числовую ось данными значениями на три интервала и раскрываем знак модуля на каждом из них и получаем:

 

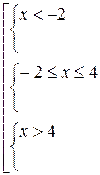
Ответ:

 

3) | x +2|-| х -4|>-6;

Находим нули модулей:

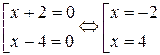
Разбиваем числовую ось данными значениями на три интервала и раскрываем знак модуля на каждом из них и получаем:

 

Ответ:

 

4) | x +2|-| х -4|£-6.

Находим нули модулей:

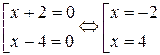
Разбиваем числовую ось данными значениями на три интервала и раскрываем знак модуля на каждом из них и получаем:

Ответ:

Домашнее задание

Действительные числа. Множества. Практика

Тест 2

Вопрос 1Определить множество (-2; 4)È[1; 6]
а.) (-2; 6)	б.) (-2; 6]	в.) [1; 4)	г.) [1; 6]
Вопрос 2Определить множество (-2; 4)Ç[1; 6]
а.) [1; 4)	б.) (1; 4)	в.) (-2; 6]	г.) (-2; 6)
Вопрос 3Определить множество (-2; 4)\[1; 6]
а.) (-2; 1]	б.) (-2; 6)	в.) (4; 6]	г.) (-2; 1)
Вопрос 4Определить множество [1; 6]\(-2; 4)
а.) (4; 6)	б.) (4; 6]	в.) [4; 6]	г.) (-2; 6]
Вопрос 5Определить множество (-3; 1]È(1; 4)
а.) (-3; 4)	б.) (-3; 1]È(1; 4)	в.) (-3; 1)	г.) [1; 4)
Вопрос 6Определить множество (-3; 1]Ç(1; 4)
а.) {1}	б.) (-3; 4)	в.) Æ	г.) (-3; 1]È(1; 4)
Вопрос 7Определить множество (-3; 1]\(1; 4)
а.) {1}	б.) (-3; 1]	в.) (-3; 1)	г.) Æ
Вопрос 8Определить множество (1; 4)\(-3; 1]
а.) [1; 4)	б.) Æ	в.) (-3; 4)	г.) (1; 4)
Вопрос 9Определить множество [0; 2]È(0; 6)
а.) (0; 6)	б.) [0; 2]	в.) [0; 6)	г.) (0; 2]
Вопрос 10Определить множество [0; 2]Ç(0; 6)
а.) (0; 6)	б.) [2; 6)	в.) (0; 2]	г.) [0; 2]
Вопрос 11Определить множество [0; 2]\(0; 6)
а.) {0}	б.) Æ	в.) [2; 6)	г.) (2; 6)
Вопрос 12Определить множество (0; 6)\[0; 2]
а.) Æ	б.) (2; 6)	в.) [2; 6)	г.) (0; 6)
Вопрос 13Определить множество [0; 6]\(0; 2)
а.) [2; 6]	б.) (2; 6]	в.) {0}È(2; 6]	г.) {0}È[2; 6]
Вопрос 14Определить множество (0; 2)\[0; 6]
а.) R	б.) {0}	в.) Æ	г.) (2; 6)
Вопрос 15Укажите верное равенство
а.) А ÈÆ= А	б.) А ÈÆ=Æ	в.) А ÈÆ= R	г.) А ÈÆ= Ā
Вопрос 16Укажите верное равенство
а.) А ÇÆ= А	б.) А ÇÆ=Æ	в.) А ÇÆ= R	г.) А ÇÆ= Ā
Вопрос 17Укажите верное равенство
а.) А \Æ= А	б.) А \Æ=Æ	в.) А \Æ= R	г.) А \Æ= Ā
Вопрос 18Укажите верное равенство
а.) Æ\ A = А	б.) Æ\ A =Æ	в.) Æ\ A = R	г.) Æ\ A = Ā
Вопрос 19Укажите верное равенство
а.) А È R = А	б.) А È R =Æ	в.) А È R = R	г.) А È R = Ā
Вопрос 20Укажите верное равенство
а.) А Ç R = А	б.) А Ç R =Æ	в.) А Ç R = R	г.) А Ç R = Ā
Вопрос 21Укажите верное равенство
а.) А \ R = А	б.) А \ R =Æ	в.) А \ R = R	г.) А \ R = Ā
Вопрос 22Укажите верное равенство
а.) R \ А = А	б.) R \ А =Æ	в.) R \ А = R	г.) R \ А = Ā
Вопрос 23Факториал натурального числа n - это
а.) n!=1·2·…·(n -1)· n	б.) n!=2·…·(n -1)· n	в.) n!=1·2·…· n ·…	г.) n!=1·2·…·(n -1)
Вопрос 24Укажите верное равенство
а.) n!= n	б.) 0!=1	в.) 0!=0	г.) 1!=1
Вопрос 25Укажите верное равенство
а.) (-3)!=-6	б.) (-3)!=6	в.) (-3)!=0	г.) (-3)!=Æ

где È - объединение; Ç - пересечение; \ – разность; Ā – дополнение множества А до множества R.

Комплексные числа. Теория

Тест 3

Вопрос 1Действительной частью комплексного числа z = x + iy является
а.) y	б.) x	в.) i	г.) iy
Вопрос 2Мнимой частью комплексного числа z = x + iy является
а.) y	б.) x	в.) i	г.) iy
Вопрос 3Если в комплексном числе z = x + iy x =0, то комплексное число называется
а.) действительным	б.) простым	в.) мнимым	г.) чисто мнимым
Вопрос 4Если в комплексном числе z = x + iy у =0, то комплексное число называется
а.) действительным	б.) сопряжённым	в.) мнимым	г.) чисто мнимым
Вопрос 5Два комплексных числа z 1 =х 1 +iу 1 и z 2 =х 2 +iу 2, считаются равными z 1 =z 2,
а.) х 1 =х 2	б.) у 1 =у 2	в.)	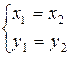г.)
Вопрос 6Сопряжёнными комплексными числами являются
а.) z =- x - iy и ` z = x + iy	б.) z = x - iy и ` z = x + iy	в.) z = x + iy и ` z = x - iy	г.) z =- x + iy и ` z = x + iy
Вопрос 7Действительной осью комплексной плоскости является
а.) ось ординат	б.) ось абсцисс	в.) ось О х	г.) ось О у
Вопрос 8Мнимой осью комплексной плоскости является
а.) ось ординат	б.) ось абсцисс	в.) ось О х	г.) ось О у
Вопрос 9Длина вектора изображающего комплексное число z = x + iy называется
а.) расстоянием	б.) модулем	в.) аргументом	г.) углом
Вопрос 10Величина угла между положительным направлением действительной оси и вектором, изображающем комплексное число называется
а.) расстоянием	б.) модулем	в.) аргументом	г.) углом
Вопрос 11Форму записи комплексного числа z = x + iy называют
а.) тригонометрической	б.) показательной	в.) экспоненциальной	г.) алгебраической
Вопрос 12Форму записи комплексного числа z = rеij называют
а.) тригонометрической	б.) показательной	в.) экспоненциальной	г.) алгебраической
Вопрос 13Форму записи комплексного числа z = r (cosj+isinj) называют
а.) тригонометрической	б.) показательной	в.) экспоненциальной	г.) алгебраической
Вопрос 14Аргумент комплексного числа считается положительным, если он отсчитывается от
а.) положительного направления оси абсцисс против часовой стрелки	б.) положительного направления оси абсцисс по часовой стрелке	в.) положительного направления оси ординат против часовой стрелки	г.) положительного направления оси ординат по часовой стрелке
Вопрос 15Аргумент комплексного числа считается отрицательным, если он отсчитывается от
а.) положительного направления оси абсцисс против часовой стрелки	б.) положительного направления оси абсцисс по часовой стрелке	в.) положительного направления оси ординат против часовой стрелки	г.) положительного направления оси ординат по часовой стрелке
Вопрос 16Два комплексных числа z = а + ib и ` z = а - ib, имеют
а.) противоположные модули и равные аргументы	б.) равные модули и равные аргументы	в.) противоположные и модули, и аргументы	г.) равные модули и противоположные аргументы
Вопрос 17Два комплексных числа z = а + ib и ` z =- а + ib, имеют
а.) разные модули и смежные аргументы	б.) равные модули и равные аргументы	в.) равные модули и противоположные аргументы	г.) равные модули и смежные аргументы
Вопрос 18Аргумент комплексного числа z =0+ i 0 считается равным
а.) любому значению	б.) 0	в.) p	г.) 2p
Вопрос 19Укажите верное равенство
а.) i 2=-1	б.) i 2=1	в.) i 3=- i	г.) i 4=1
Вопрос 20Комплексное число z=х+iу равно нулю z= 0 тогда и только тогда, когда
а.) х= 0	б.) у= 0	в.) х= 0 или у= 0	г.) х= 0 и у= 0

 

В.С.Шипачёв. Задачник по высшей математике.

 

Решить в тетради:

 

Номера заданий	Страница в задачнике
8; 9; 10; 11
34; 39; 43; 44; 45; 46

 

Указание:

При решении уравнений и неравенств с вложенными друг в друга модулями, необходимо методом интервалов раскрыть сначала внутренние модули, упростить, а затем раскрывать оставшиеся внешние модули.

 

Например:

Решить уравнение || x ²-4|-3 х |=6

 

Находим нули внутреннего модуля:

 

Разбиваем числовую ось данными значениями на три интервала и раскрываем знак внутреннего модуля на каждом из них и получаем:

 

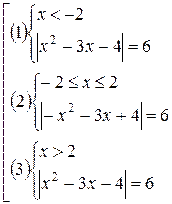
Опять находим нули модулей и раскрываем их на соответствующих промежутках:

 

Ответ: {-2; -1; 2; 5}.