движущейся коксовой частицы

КУРСОВАЯ РАБОТА

Дисциплина: Моделирование физических процессов

Тема: Математическое моделирование горения

движущейся коксовой частицы

Выполнил студент гр. 5И33/1		Е.А. Ли

Проверил		А.П. Парамонов Ю.А. Рундыгин

	“____” ______________ 2009 г.

Санкт-Петербург

Содержание

1. Введение

2. Методика расчета движения одиночной частицы в заданном поле скоростей газового потока.

2.1 Уравнение движения частицы

2.2 Основные силы, действующие на движущуюся частицу. (Сила веса, сила лобового сопротивления, сила Архимеда и др.)

3. Методика расчета горения одиночной угольной частицы

3.1 Стадии горения угольной частицы

3.2 Оценка длительности протекания отдельных стадий и методы расчета горения коксового остатка

4. Численные методы решения дифференциальных уравнений первого и второго порядка

5. Разработка блок-схемы программы и текста программы

6. Выбор шага интегрирования

7. Расчетный анализ траекторий движения горящих угольных частиц

8. Выводы и рекомендации

9. Литература

ВВЕДЕНИЕ

В данной курсовой работе исследовалось движение и горение твердой угольной частицы в топочной камере в потоке дымовых газов, влияние параметров топочного процесса на полноту сгорания топлива в топке котла. Для расчета движения и горения частицы в поле скоростей были составлены дифференциальные уравнения движения и выгорания соответственно.

Оценка траектории и скорости движения частиц необходима при расчетах выгорания частиц топлива, оптимизации аэродинамики топочной камеры с целью уменьшения выноса недогоревших частиц, при оценке зон предполагаемого эрозионного износа элементов топки, при расчете сепарации частиц топлива и их транспортировки.

Топливо- Татауровский бурый уголь марки 2БР.

Результаты были получены с помощью программы Pascal.

МЕТОДИКА РАСЧЕТА ДВИЖЕНИЯ ОДИНОЧНОЙ ЧАСТИЦЫ В ЗАДАННОМ ПОЛЕ СКОРОСТЕЙ ГАЗОВОГО ПОТОКА

При рассмотрении движения угольной частицы были приняты следующие допущения:

· Движение одиночной частицы в потоке дымовых газов;

· Движение двухмерное;

· Частица начинает движение на уровне первого яруса горелок;

· Скорость движения частицы по горизонтали в пределах 0,5 м от оси горелки по вертикали равна скорости выхода струи из горелки, скорость по вертикали равно 0;

· За пределами 0,5 метров от оси горелок по вертикали скорость частицы по горизонтали принимается равной 0.

2.1 УРАВНЕНИЕ ДВИЖЕНИЯ ЧАСТИЦЫ

Дифференциальные уравнения частицы выглядят следующим образом:

(1)

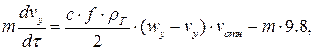
(2)

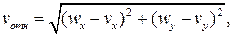
(3)

где m – масса частицы, кг;

w, v – скорости газа и частицы в проекциях на оси Х и У, м/с;

с – коэффициент сопротивления частицы;

f – площадь миделева сечения частицы, м²;

ρ_Г – плотность газа, кг/м³.

2.2 ОСНОВНЫЕ СИЛЫ, ДЕЙСТВУЮЩИЕ НА ДВИЖУЩУЮСЯ ЧАСТИЦУ

При рассмотрении движения частицы не учитывается ее выгорание, т.е. масса остается постоянной. Тогда на частицу действуют следующие силы: лобового сопротивления частицы потоку, сила веса и архимедова сила.

Сила лобового аэродинамического сопротивления – первое слагаемое уравнений справа.

Архимедовой силой в данном случае мы пренебрегаем ввиду большой разности плотностей частицы и потока.

Сила веса представлена во втором уравнении вторым слагаемым.

Коэффициент сопротивления частицы рассчитывается с помощью критерия Рейнольдса:

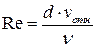
(4)

при Re<1 и

при 1<Re<1000

(5)

МЕТОДИКА РАСЧЕТА ГОРЕНИЯ ОДИНОЧНОЙ УГОЛЬНОЙ ЧАСТИЦЫ

Для расчета горения частицы использовалась эмпирическое выражение, предложенное В.И. Бабием для мелких частиц (δ≤10^{-3 м) [1].}

3.1 СТАДИИ ГОРЕНИЯ УГОЛЬНОЙ ЧАСТИЦЫ

Процесс горения твердой угольной частицы можно разбить на относительно независимые стадии: прогрев частицы до выхода или воспламенения летучих, горение летучих веществ около частицы, способствующие быстрому подъему температуры частицы, горение коксового остатка, состоящего из углерода и золы.

При горении мелкой топливной пыли стадии прогрева и выхода летучих по продолжительности составляет менее 10% общего времени горения, а время выгорания углерода кокса составляет более 90%. Поэтому в последнее время при анализе процесса горения пылеугольного факела пренебрегают стадиями прогрева частиц и выхода летучих, считать мгновенным выход летучих и их сгорание и рассматривают горение коксового остатка как горение чистого углерода, так как зола коксового остатка не оказывает существенного влияния на выгорание углерода.

3.2 ОЦЕНКА ДЛИТЕЛЬНОСТИ ПРОТЕКАНИЯ ОТДЕЛЬНЫХ СТАДИЙ И МЕТОДЫ РАСЧЕТА ГОРЕНИЯ КОКСОВОГО ОСТАТКА

Время горения коксового остатка τ_ГК, с, при малых скоростях обдувания может быть определено по следующей эмпирической зависимости [2]

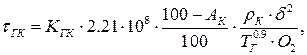
(6)

где K_гк – опытный коэффициент;

A_К – внутренняя зольность коксового остатка, %;

O₂ – объемная концентрация кислорода, %;

ρ_К – плотность коксового остатка, кг/м³.

Как было сказано выше, стадиями прогрева частицы и выхода и воспламенения летучих пренебрегаем.

Физико-химические характеристики топлив [2]: влажность на рабочую массу (W^r), зольность на сухую массу (A^d), внутренняя зольность коксового остатка (A^k), выход летучих на сухую беззольную массу (V^daf), низшая теплота сгорания на сухую беззольную массу (Q^daf_i), плотность коксового остатка (ρ_К) и опытный коэффициент (K _гк) представлены в таблице 1.

Таблица 1 – Физико-химические характеристики углей

Марка угля	W^r, %	A^d, %	A^k, %	V^daf, %	Q^daf_i, МДж/кг	ρ_К, кг/м³	K _гк
Донецкий, А Донецкий, Г Донецкий, ГСШ Донецкий, Ж Донецкий, К Кузнецкий, СС2СС Кузнецкий, Д Кузнецкий, Г Назаровсий, 2Б Березовский 2Б Ирша-Бородинский Бикинский, 2Б Реттиховский, 1Б Экибастузский	2.3 1.1 2.8 1.0 0.6 2.6 6.2 6.6 12.4 10.1 10.7 9.0 8.3 1.4	4.6 4.9 2.1 10.4 3.4 3.6 12.1 7.5 8.8 4.7 9.3 18.1 25.5 29.1	4.7 7.3 3.3 12.8 4.1 4.4 18.7 11.2 15.6 8.8 15.8 31.9 44.6	2.6 34.7 37.2 21.1 18.3 19.0 40.2 35.8 47.8 48.7 45.3 52.8 57.5 30.1	33.56 32.97 32.05 33.89 34.65 34.05 30.56 31.06 26.17 26.54 27.13 24.44 25.83 30.87		1.0 0.8 0.5 0.6 0.7 1.05 0.9 0.9 1.4 1.4 1.2 1.6 2.0 0.9

Дифференциальное уравнение изменения размера угольной частицы в зависимости от параметров процесса может быть получено из уравнения (6)

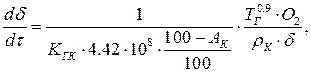
(7)

4. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО И ВТОРОГО ПОРЯДКА

Решение полученных дифференциальных уравнений для движения и выгорания частицы производится по методу Эйлера. Сущность метода заключается в том, что мы задаём шаг интегрирования и получаем приращение функции и новое значение функции.

5. РАЗРАБОТКА БЛОК-СХЕМЫ ПРОГРАММЫ И ТЕКСТА ПРОГРАММЫ

Рисунок 1. Укрупненная блок-схема программы

Текст программы

uses graph, crt;

var

d,dd, m,f,c,Ax,Ay,O2, Tg, denP,denG, Vkg,

x, y, Ht, Hg, Wg, Wgor, dT, Ta, Vx, Vy: double;

mast,Re, Wx,Wy,Votn: double;

Tgk, Kgk, Akc, denPk,Br, Wr,Ar,Vr, Vg: double;

at,bt, time: double;

g1,g2,xx,yy: integer;

s1, s2: string;

fff: text;

label

met_end, met1;

begin

d:=872e-6;

denP:=1200; {kg/m3}

Wr:=34.3;

Ar:=7.3;

Vr:=45;

Vg:=6.104;

Kgk:=1.8;

Akc:=22;

Br:=211.3;

Ht:=44.9;

at:=22.2;

bt:=12.285;

O2:=21;

Hg:=Ht*0.2;

Wgor:=20;

x:=0.001;

y:=Hg;

Vx:=Wgor;

Vy:=0;

dT:=0.0005;

{=================}

time:= 0;

denPk:=denP*(100-Wr-Vr)/100;

{========================================================}

g1:=VGA; g2:=VGAHi;

initgraph(g1, g2, '');

MAST:=getmaxy/Ht;

met1:

xx:=round(x*mast);

yy:=getmaxy-round(y*mast);

putpixel(xx,yy,15);

{}

m:=denP*d*d*d*Pi/6;

Tg:=-y*1.116e0 + 1.553e3;{(-8.500e-3)*y+1.525e3;

DenG:=1.3*273/(Tg+273);

Vkg:=Tg*(4.405e-11*Tg + 1.211e-7) + 1.36e-6; {m2/s}

Wg:=Br*1000*Vg*(Tg+273)/(3600*273*at*bt);

Wy:=Wg;

{=====================}

if y < Hg then O2:=21

else O2:=(-0.4872)*y + 25.375;

{=====}

if abs(Hg-y)<0.5 then Wx:=Wgor

else Wx:=0;

Votn:=sqrt(sqr(Wx-Vx)+sqr(Wy-Vy));

Re:=d*Votn/Vkg;

if Re<1 then c:=24/Re

else c:=24/Re+ 4/exp(ln(Re)/3);

f:=Pi*d*d/4;

Ax:=c*f*denG*(Wx-Vx)*Votn/(2*m);

Ay:=c*f*denG*(Wy-Vy)*Votn/(2*m) - 9.8;

Vx:=Vx+Ax*dT;

Vy:=Vy+Ay*dT;

x:=x+Vx*dT;

y:=y+Vy*dT;

{===============================================================}

dd:=-exp(0.9*ln(Tg)) * O2 / (Kgk*2*2.21e8*((100-Akc)/100)*denPk*d);

d:=d + dd*dT;

time:=time + dT;

{===============================================================}

{ time, x, y, d }

if d < 50e-6 then begin

xx:=round(x*mast);

yy:=getmaxy-round(y*mast);

setcolor(red);

circle(xx, yy, 2);

goto met_end;

end;

if (y<Ht) and (not KEYPRESSED) and (y>0) then goto met1;

{=================================================================}

met_end:

str(x:-10:6, s1);

outtextXY(400,20, 'X='+S1);

str(y:-10:6, s2);

outtextXY(400,30, 'Y='+S2);

close(fff);

readkey;

{===============================}

end.

ВЫБОР ШАГА ИНТЕГРИРОВАНИЯ

Шаг интегрирования по времени выбирается таким, чтобы его значение не оказывало влияния на погрешность измерений.

Для выбора шага был построен график зависимости погрешности определения координаты от шага интегрирования для движения и выгорания частицы размером 860 мкм (Рисунок 2)

Рисунок 2. Погрешность определения координаты в зависимости от шага по времени

Из графика 1 видно, что шаг интегрирования перестаёт влиять на погрешность при dt=0,0005с, поэтому выбираем этот шаг для дальнейших расчётов.

Скорость газового потока, концентрация кислорода, температура газа и геометрия топочной камеры берутся из курсового проекта по расчету котлоагрегата.

7. РАСЧЕТНЫЙ АНАЛИЗ ТРАЕКТОРИЙ ДВИЖЕНИЯ ГОРЯЩИХ УГОЛЬНЫХ ЧАСТИЦ.

По результатам работы составленной программы были получены следующие значения:

· Диаметр частицы, при которой начинается унос, составляет 872 мкм.

· Диаметр частицы, при которой начинается провал, составляет 2017 мкм.

Траектории движения этих частиц представлены на рисунке 3 и 4 соответственно.

Рисунок 3

Траектория движения частицы при уносе

Рисунок 4

Траектория движения частицы при уносе при провале

Рисунок 5. Размер уноса частицы в зависимости от избытка воздуха и температуры на выходе из топки

На рисунке 5 изображена зависимость размера частицы, при которой начинается унос, от температуры на выходе из топки и избытка воздуха. Из рисунка видно, что с увеличением температуры размер частицы, при которой начинается унос, уменьшается при одинаковом избытке воздуха. Так же при увеличении избытка воздуха размер частицы, при которой начинается унос, увеличивается.

ВЫВОДЫ И РЕКОМЕНДАЦИИ

Принятые параметры топочного процесса (избыток воздуха и температура на выходе из топки) дают следующие значения

Диаметр частицы при уносе - 872 мкм
Диаметр частицы, при которой будет провал- 2017 мкм.

Были построены траектории движения соответствующих частиц.

Анализируя полученный результат, можно сделать вывод, что для снижения уноса следует увеличить избыток воздуха в топке и повысить температуру на выходе из нее, однако это приведет к увеличению затрат на тягодутьевые машины, а так же может привести к плавлению угля и, соответственно, шлакованию поверхностей нагрева.

Поэтому выбранный вариант (при температуре 1052^о и избытке воздуха 1.2) будет оптимальным при данных размерах топки.

Литература

1 Основы практической теории горения: под ред. В.В. Померанцева.- Л.: Энергоатомиздат, 1986.- 309 с.

2 Бабий В.И., Куваев Ю.Ф. Горение угольной пыли и расчет пылеугольного факела. - М.: Энергоатомиздат, 1986. - 208 с.