Задача 1
В распределительном пункте (РП) установлено пять автоматических выключателей. Нормальная работа потребителей обеспечивается при их исправном состоянии. При монтаже РП выбирались из партии объемом в 1000 штук, в которой било 950 исправных выключателей и 50 неисправных. Найти вероятность исправной работы РП
Решение.
Число элементарных событий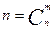 
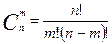
Обозначим: событие А есть исправная работа РП. Оно осуществляется, если все выключатели выбраны из числа исправных.
Число элементарных событий, благоприятствующих событию А, равно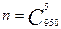 
. Следовательно, 
.
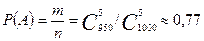Задача 2
Вероятность выхода из строя электрического прибора равна Р = 0,01. Для повышение надежности в прибор поставлены m дублирующих ветвей. Определить, во сколько раз (k) увеличится надежность прибора, если под ней понимать вероятность безотказной работы.
Решение.
Вероятность того, что откажут все параллельные ветви (событие А):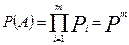 
Вероятность того, что не откажет хотя бы одна из параллельных ветвей (событие В):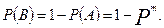 
Надежность одной ветви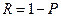 
.
Искомая величина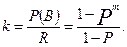 
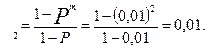
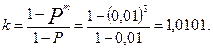
Задача 3
Две цепи электроснабжения работают параллельно на общую нагрузку.
Рисунок - Схема питания
Вероятность аварийного простоя одной цепи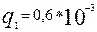 
, второй 
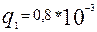. Принимая аварийные состояния цепей независимыми, определить вероятность аварийного простоя двухцепной электропередачи для двух случаев:
а) отказ электропередачи происходит при отказе оной из цепей (любой);
б) отказ электропередачи происходит при отказе только обеих цепей.
Решение.
а) На основании теоремы сложения вероятностей (логическая схема «или»)
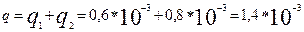
б) На основании теоремы умножения вероятностей (логическая схема «и»)
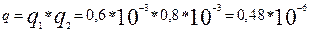
Вероятность безотказной работы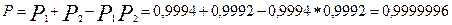 
Задача 4
Питание потребителя осуществляется по одной цепи, состоящей из кабельной линии, трансформатора, выключателя.
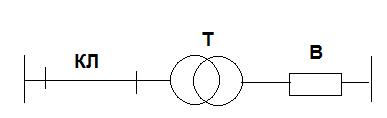
Рисунок- Схема питания
Вероятность безотказной работы за время t для этих элементов: Ркл = 0,7, Рт = 0,8, Рв = 0,9. Отказ любого элемента приводит к перерыву питания, причем отказы взаимно независимы. Найти вероятность безотказной работы передачи.
Решение.
Обозначим: Акл – безотказная работа линии, Ат – трансформатора, Ав – выключателя, А – всей системы. По теореме умножения для независимых событий
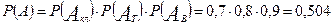
Задача 5
Питание потребителя осуществляется по одной цепи, состоящей из кабельной линии, трансформатора, выключателя.
Рисунок- Схема питания
Вероятность безотказной работы за время t для этих элементов: Ркл = 0,7, Рт = 0,8, Рв = 0,9. Отказ любого элемента приводит к перерыву питания, причем отказы взаимно независимы. Найти вероятность отказа передачи.
Решение.
Обозначим: Акл – безотказная работа линии, Ат – трансформатора, Ав – выключателя, А – всей системы. По теореме умножения для независимых событий
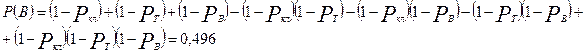
Задача 6
Силовые трансформаторы изготавливаются тремя заводами, причём вероятность того, что трансформатор выпущен на первом заводе, равна 0,2, на втором – 0,3, на третьем — 0,5. Вероятность того, что при определенных условиях работы трансформатор сохранит работоспособность в течение 25 лет, для первого, второго и турьего заводов соответственно равны: 0,9; 0,92; 0,808. Чему равна вероятность того, что поступивший для монтажа трансформатор сохранит работоспособность в течение 25 лет?
Решение. Этот трансформатор может оказаться с первого завода (событие Н1), со второго (событие Н2), с третьего (событие Н3). Интересующее нас событие А имеет вероятность
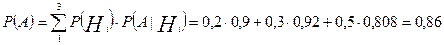
Задача 7
Пропускная способность канала связи в система телемеханики зависит от появления ошибки внутри канала (рисунок 2.3) На вход канала могут подаваться два сигнала х1 и х2. На выходе принимаются соответственно y1и y2.40% времени канал занят передачей сигнала х1 и 60% времени — сигнала х2. Вероятность безошибочной передачи сигнала х1 как у1 равна 0,75. Вероятность того, что входной сигнал х1 будет ошибочно принят как у2, равна 0,25. Аналогично вероятность того, что сигнал, первоначально переданный как х2 будет принят как у2 и у1, равна соответственно 0,9 и 0,1. При заданных условиях получен выходной сигнал у1. Какова вероятность того, что исходный сигнал был х1?
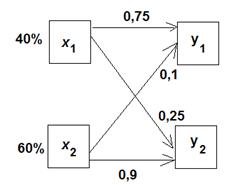
Рисунок – Схема канала связи
Решение. Вероятности гипотез Р(Н1) = 0,4, Р(Н2) = 0,6. Условные вероятности события «получен выходной сигнал у1» равны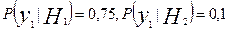 
По теореме Бейеса
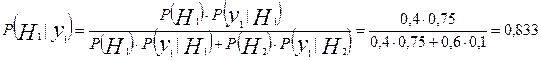
Задача 8
Энергосистема ограничивает военный объект в потреблении энергетической мощности. При этом в течение года возможны дефициты в 5, 10 и 15 МВт с вероятностями соответственно 0,001. 0.0004 и 0,0002. Определить математическое ожидание недоотпуска электроэнергии военному объекту за год.
Решение.
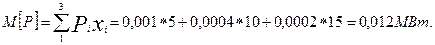
В году 8760 часов.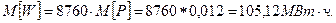 
Задача 9
В результате испытания 36 образцов аппаратуры была зафиксирована 231 неисправность. При этом каждый из испытуемых образцов проработал в среднем по 19 часов. Определить среднюю наработку на отказ.
Решение
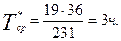
Задача 10
Имеется восстанавливаемая система, у которой параметр потока отказов l =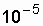 
1/ч = const, средняя интенсивность восстановления 
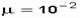1/ч. Определить, на сколько повысится надежность этой системы за счет более высокой организации работы ремонтного персонала, если интенсивность восстановления системы повысилась вдвое (сократилось вдвое время восстановления).
Решение.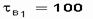 
ч; 
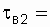50 ч. Коэффициент готовности системы до улучшения организации труда ремонтного персонала составлял
.
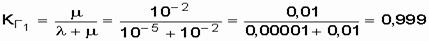При улучшенной организации труда
.
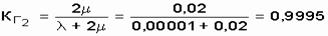Задача 11
Восстанавливаемая система состоит из трех последовательно включенных элементов с параметрами надежности:
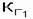= 0,6; 
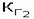= 0,8; 
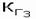= 0,7. Известно, что 
.
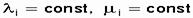Определить коэффициент надежности.
Решение. Подставив заданные значения коэффициентов готовности в выражение КГ системы, получим
.
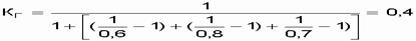Задача 12
Рассмотрим блочные схемы питания однотрансформаторных подстанций 110 кВ (рисунок 1.1). Отказ СЭС таких подстанций вызывается отказом любого из элементов системы. Частота отказов этих элементов приведена ниже:
| № п\п | |||||||
| λ, 1/год | 0,02 | 0,01 | 1,0 | 0,02 | 0,01 | 0,01 | 0,01 |
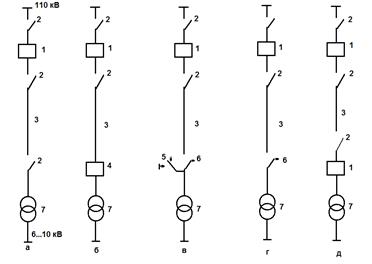
Рисунок – Схемы питания однотрансформаторных подстанций
Решение.
В соответствии с формулой модели последовательного соединения вычислим частоту погашения подстанций при всех вариантах схемы электроснабжения:
λс =λ1+3λ2+λ3+λ7= 1,06 1/год
λс =λ1+3λ2+λ3+λ4+λ7= 1,08 1/год
λс =λ1+3λ2+λ3+λ5+λ6+λ7= 1,08 1/год
λс =λ1+3λ2+λ3+λ6+λ7= 1,07 1/год
λс =2λ1+3λ2+λ3+λ7= 1,08 1/год
Эти результаты показывают, что наибольшей надежностью обладает схема а), а доминирующее влияние на частоту погашений оказывает поврежденность воздушной линии λ3.
Задача 13
Рассмотрим схему секции РУ-6 кВ. от которой питается 21 отходящая линия. Частота отказов с короткими замыканиями для выключателей оценивается величиной λв =0.003 1/год, а частота отказов с коротким замыканием для сборных шин λш =0.03 1/год.
Решение. Частота кратковременных погашений секции из-за коротких замыканий на шинах и выключателях составляет:
λс = 22λв + λш =0.066 +0.03 = 0.096 1/год.
Таким образом, частота погашений секции 6 кВ определяется числом присоединений и надежностью выключателей.
Задача 14
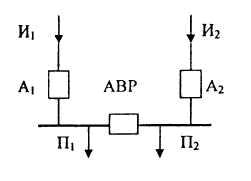
Потребители питаются от двух независимых источников. Один источник включен постоянно, второй включается действием АВР (рисунок 1.2). Вероятность безотказной работы источников в течение расчетного периода времени равна Р(И1)=0,99.Вероятность застать резервный источник в работоспособном состоянии в любой момент времени Р(И2)=0,99. Вероятность отказа в отключении Q(A1)=0,05,во включении Q(A2)=0,01. определить вероятность безотказной работы СЭС в течение расчетного времени с учетом возможности использования резервного источника, считая, что вероятность отказа резервного источника за время восстановления рабочего можно пренебречь.
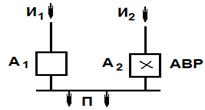
Рисунок – Схема питания
Решение. В соответствии с условиями запишем: безотказность в отключении P(A1)= 1 – Q(A1)= 0,95; безотказность включения P(A2)= 1 – Q(A2)= 0,99; условные вероятности Q(S|A1A2)=1; Q(S|A1A2)=1; Q(S|A1A2)=1.
Вероятность отказа системы при отсутствии отказов аппаратуры определяется как произведение вероятности отказа рабочего источника и вероятности аварийного простоя резервного:
Q(S|A1A2)=(1 – 0,9)(1 – 0,99)= 0,001.
По формуле 1 получим
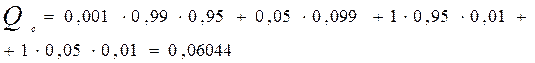
Искомая вероятность безотказной работы Рс= 1- Qc = 0,93956.
Задача 15
Рассмотрим элемент с равномерным распределением элементов в конце периода Тпл составляет 75% числа работоспособных элементов в начале периода Тпл.
Решение. Тогда
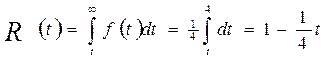
Откуда R(Тпл) = 0,75, т.е число работоспособных элементов в конце периода Тпл составляет 75% числа работоспособных элементов в начале периода Тпл.
Зависимость интенсивности отказов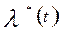 
при Тпл = 1 год
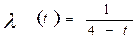
Тогда средняя интенсивность отказов будем решать по формуле
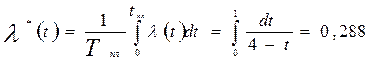1/год.
Средняя наработка на отказ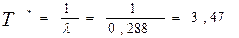 
года.
Задача 16
Рассмотрим элемент с равномерным распределением срока службы f(t) = ¼ 1/год при 0< t > 4 года и периодичности предупредительных ремонтов Тпл = 1 год.
Решение:
Тогда
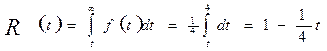
Откуда R(Тпл) = 0,75, т.е число работоспособных элементов в конце периода Тпл составляет 75% числа работоспособных элементов в начале периода Тпл.
Зависимость интенсивности отказов 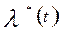при Тпл = 1 год
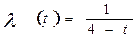
Тогда средняя интенсивность отказов будем решать по формуле
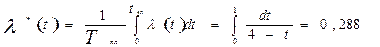1/год.
Средняя наработка на отказ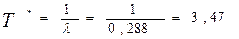 
года.
При отсутствии предупредительного ремонта наработка на отказ составила бы
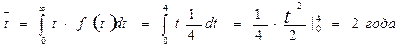
что почти вдвое больше начального значения. При λ = 0,5 1/год.
Таким образом. Безотказность элемента существенно увеличивается при условии идеального мгновенного ремонта или замены.
Задача 17
Выпущена партия резисторов 100000 штук. Вероятность того, что резистор имеет брак, р = 0,0001. Найти вероятность того, что в партии ровно пять бракованных резисторов.
Решение.
А = Np = 100000 ∙ 0,0001 = 10.
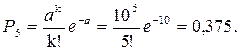
Задача 18
Определить вероятность того, что за 500 ч работы произойдет два отказа в сложном изделии, если известно, что интенсивность отказов λ = 1 ∙ 10-3.
Решение.
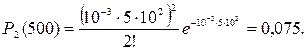
Задача 19
Время безотказной работы силового трансформатора при перегрузке распределено по экспоненциальному закону f = 0,02e-0,02t , где t – время, ч. Найти вероятность того, что трансформатор в перегрузочном режиме проработает безотказно в течение 100 ч.
Решение.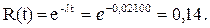 
Среднее время безотказной работы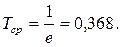 
Задача 20
Наблюдения за эксплуатацией 10 электродвигателей выявили, что первый проработал до отказа 800 ч, второй – 1200 и далее соответственно 900, 1400, 700, 950, 750, 1300, 850 и 1500 ч. Определить наработку двигателей до внезапного отказа.
Решение.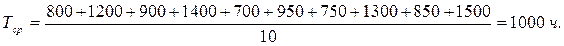 
Задача 21
При эксплуатации 100 трансформаторов в течение 10 лет произошло два отказа, причем каждый раз отказывал новый трансформатор. Определить интенсивность отказов трансформатора за период наблюдения.
Решение.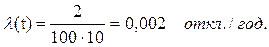 
Задача 22
Изменение числа отказов ВЛ из-за производственной деятельности сторонних организаций по месяцам года представлено следующим образом:
| месяц | я | ф | м | а | м | и | и | а | с | о | н | д |
| n (кол-во повреждений) |
Определить среднемесячную интенсивность отказов.
Решение.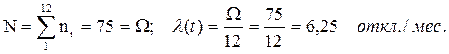 
Задача 23
Трансформатор отказал, проработав около года. После устранения причины отказа он проработал еще три года и опять вышел из строя. Определить среднюю наработку трансформатора на отказ.
Решение.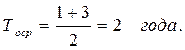 
Задача 24
Электротехническое устройство состоит из трех элементов. В течение первого года эксплуатации в первом элементе произошло два отказа, во втором – один, в третьем отказов не было. Определить параметр потока отказов.
Решение.
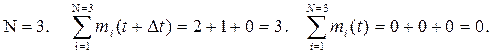
Откуда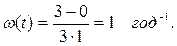 
Задача 25
За год эксплуатации зарегистрирован m =21 случайных отказов воздушных выключателей и = 330 кВ при отключении ими коротких замыканий. Число эксплуатируемых выключателей в этом году составляло N = 1750 шт. Оценить средний параметр потока отказов и его доверительные границы с доверительной вероятностью β = 0,95.
Решение. Примем гипотезу об экспоненциальном распределении для наработки на отказ, используя следующие выражения и соответствующие таблицы:
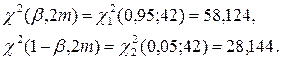
Далее вычисляются верхнее ωв, нижнее и среднее `w значения искомых величин
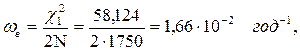
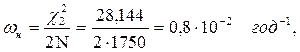
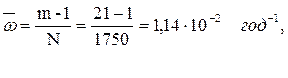
Задача 26
Определить показатели надежности СЭС с двумя кабельными линиями 6 кВ: λ = 0,2 год-1; длительность восстановления t = 24 ч; t = 1 год.
Решение. Для одного кабеля: t = 24 ч = 1/365 года, m = 365 год-1.
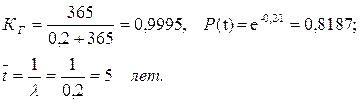
При двух кабелях и резервировании, замещением КГ = 0,9999997; Т = 9100 лет. Р(t) = 0,9999.
Задача 27
Рассмотрим элемент с равномерным распределением срока службы f(t) = 1/4 год-1 при 0< t ≤ 4 года и периодичности предупредительных ремонтов Т пл = 1 год.
Решение.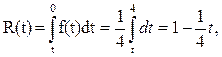 
Откуда R (Т пл) = 0,75, т.е. число работоспособных элементов в конце периода Т пл составляет 75% числа работоспособных элементов в начале периода Т пл.
Зависимость интенсивности отказов λ*(t) при Т пл = 1 год: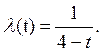 
Задача 28
В течение пяти лет наблюдений (t = 5) из семи работающих на электростанции генераторов N0 = 7, отказало два N(t) = N(5) = 2.
Решение. ВБР: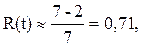 
Вероятность отказа: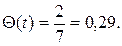 
Задача 29
При эксплуатации 70 сухих трансформаторов в течение 10 лет произошло пять отказов, причем каждый раз отказывал новый трансформатор.
Решение. Интенсивность отказов: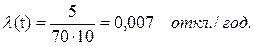 
Задача 30
Проверим гипотезу об экспоненциальном распределении длительности работы 200 ламп накаливания с помощью критерия хи-квадрат Пирсона. Результаты наблюдений представлены таблицей и гистограммой.
| Номер разряда | Границы разряда ti – ti+1, ч | Численность разряда mi |
| 0…300 | ||
| 300…600 | ||
| 600…900 | ||
| 900…1200 | ||
| 1200…1500 | ||
| 1500…1800 | ||
| 1800…2100 | ||
| 2100…2400 | ||
| 2400…2700 | ||
| 2700…3000 | ||
| 3000…3300 | ||
| более 3300 |
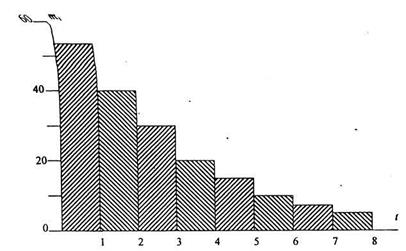
Гистограмма продолжительности работы ламп накаливания
Решение. Плотность предполагаемого распределения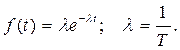 
Уровень значимости критерия примем α = 1 – β = 0,005. При оценке математического ожидания наработки на отказ М *[ t ] берутся середины разрядов
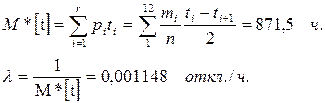
Вычисляем χ2 = 4,495. Здесь: k = 12 – 3 = 9,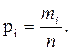 
По таблицам при α = 0,05 находим Р (χ2 ≥ χ2q, k) = 0,808. Гипотеза о согласии с экспоненциальным законом распределения не отвергается. Отклонения малы.
Задача 31
Рассмотрим схему питания однотрансформаторной подстанции 110 кВ. Одноименные элементы в схеме имеют одинаковые показатели надежности. Отказ системы происходит при отказе любого из элементов. Частоты отказов элементов приведены в таблице. Определить ожидаемую интенсивность отказов схемы и среднюю наработку на отказ.
| № элемента | ||||
| λ, год-1 | 0,02 | 0,01 | 1,0 | 0,015 |
Решение. В соответствии с моделью последовательного соединения элементов и формул интенсивность погашений потребителя составит:
Λ = 2λ1 + 3λ2 + λ3 + λ4 = 2 ∙ 0,02 + 3 ∙ 0,01 + 1,0 + 0,015 = 1,085 год-1.
Средняя наработка на отказ: Тср = 1/Λ = 1/1,085 = 0,92 года или 8073 ч.
Задача 32
Рассмотрим схему секции РУ-6 кВ, от которой питается 10 отходящих линий. Интенсивность отказов выключателей, сопровождающихся короткими замыканиями λQ = 0,003 год-1; интенсивность отказов сборных шин с короткими замыканиями на одно присоединение λш = 0,001 год-1. Определить интенсивность погашений секции РУ.
Решение. Частота погашений секции из-за коротких замыканий составляет
Λ = (10 + 1) λQ + (10 + 1) λш = 11∙0,003 + 11∙0,001 = 0,044 год-1. Следовательно, интенсивность погашений секции РУ-6 кВ определяется числом присоединений и надежностью выключателей.
Задача 33
Потребители питаются от двух независимых источников. Один источник включен постоянно, второй включается действием АВР.
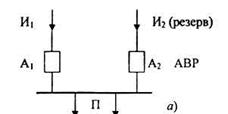
ВБР каждого источника в течение расчетного периода времени равна Р (И1) = 0,9. Вероятность застать резервный источник в работоспособном состоянии в любой момент времени Р (И2) = 0,99. Вероятность отказа в отключении поврежденного источника Q (А1) = 0,05, а во включении резервного - Q (А2) = 0,01. Требуется определить ВБР СЭС в течение расчетного времени с учетом использования резервного источника и считая, что вероятностью отказа резервного источника за время восстановления рабочего можно пренебречь.
Решение. В соответствии с условием запишем: безотказность в отключении поврежденного элемента: Р (А1) = 1 - Q (А1) = 0,95; безотказность включения резервного: Р (А2) = 1 - Q (А2) = 0,99; условные вероятности отказов системы электроснабжения: Q (S |`A1 A2) = 1; Q (S|А1 `A2) = 1; Q (S |`A1 `A2) = 1.
Вероятность отказа системы при отсутствии отказов аппаратуры определяется как: Q (S |A1A2) = (1 – 0,9) ∙ (1 – 0,99) = 0,001. По формуле:
Q c1 = 0,001∙0,99∙0,95 + 1∙0,05∙0,099 + 1∙0,95∙0,01 + 1∙0,05∙0,01 = 0,06044.
Искомая ВБР: Р с1 = 1 – Q с1 = 0,93956. В соответствии:
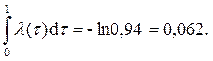
Так как λ(t) = const, то λ1 = 0,062 1/год и Тср1 = 1/λ1 = 16,13 года.
Задача 34
Потребители могут быть подключены к двум различным секциям сборных шин. Вероятность отказа источников и их аварийного простоя, а также вероятности отказов аппаратуры – как и в предыдущем примере. Секционный выключатель осуществляет АВР секции, оставшейся без питания, за счет соседней секции и ее источника. Определить вероятность бесперебойного электроснабжения любого из потребителей этой системы.
Решение. В соответствиис условиями работы схемы: вероятность отказа в отключении поврежденного источника: Q (A1) = 2∙0,05 = 0,1, так как отказать может и И1 и И2. Безотказность отключения: Р (А1) = 1 - Q (A1) = 0,95. Вероятность отключения резервного источника: Q (А2) = 0,01. Безотказность включения резерва: Р (А2) = 1 - Q (A2) = 0,99. Каждый потребитель может быть присоединен к любой секции с вероятностью 0,5. Условные вероятности нарушения электроснабжения половины присоединенной мощности равны Q (S |`A1 A2) = 1; Q (S|А1 `A2) = 1; Q (S |`A1 `A2) = 0,5. При отсутствии отказов аппаратуры отказ системы происходит при наложении отказа одного из источников на аварийный простой другого: Q (S |A1A2) = 2(1 – 0,9) ∙ (1 – 0,99) = 0,002. По формуле: Q с = 0,002∙0,9∙0,99 + 0,5∙0,1∙0,99 + 0,5∙0,9∙0,01 + 0,5∙0,1∙0,01 = 0,05628. Искомая ВБР: Р с = 1 – Q с = 0,94372. Величины λ и Т ср вычисляются аналогично предыдущему примеру: λ2 = 0,058 1/год и Тср2 = 1/λ2 = 17,24 года. Выигрыш надежности определяется показателями:
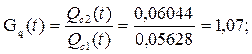
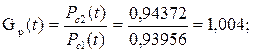
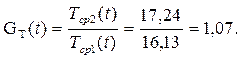
Задача 35
В схеме все элементы идентичны и ВБР p(t) = e-λt c параметром λ = 0,01 год-1. Найти ВБР этой схемы в течение 10 лет ее эксплуатации всеми рассмотренными выше методами.
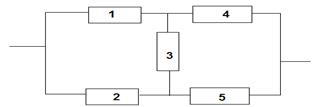
Мостиковая схема
Решение. При t = 10 имеем: р = р (10) = е -0,01∙10 = 0,9 и q = 1 – p = 0,1.
1. Методом перебора ВБР вычисляется с использованием формулы:
Р = р 5 + 5 qp 4 + 8 q 2 p 3 + 2 q 3 p 2 = 0,95 + 5∙0,1∙0,94 + 8∙0,12∙0,93 + 2∙0,13∙0,92 = 0,99.
2. То же по упрощенной формуле: Р ≈ 1 – 2 q 2 = 1 - 2∙0,12 = 0,98.
3. Методом разложения относительно особого элемента получим:
Р = р (1 – q 2)2 + q [1 – (1 – p 2)2] = 0,9 (1 – 0,12)2 + 0,1[1 – (1 - 0,92)2] = 0,98.
4. Методом минимальных путей и минимальных сечений находим верхнюю и нижнюю оценки ВБР:
(1 – q 2)2(1 – q 3)2 ≤ P ≤ 1 – (1 – p 2)2(1 – p 3)2 = (1 – 0,12)2(1 – 0,13)2 ≤ P ≤ 1 – (1 – 0,92)2(1 – 0,93)2 = 0,977 ≤ P ≤ 0,997.
Заметим, что значения ВБР, полученные методом перебора и методом разложения относительно особого элемента лежат внутри интервала, полученного методом минимальных путей и минимальных сечений.
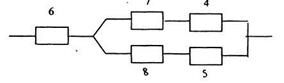
5. Преобразуем треугольник с элементами 1,2,3 в звезду с элементами 6,7,8. в результате преобразований схема приобретает следующий вид
