КОЛЕБАНИЯ, ВОЛНЫ И ОПТИКА
Пример решения задачи
1. Вдоль шнура распространяется поперечная волна, уравнение которой имеет вид  м, где
м, где  – смещение точек шнура;
– смещение точек шнура;  – время, с;
– время, с;  – координата точек шнура, м.
– координата точек шнура, м.
Найти: а) период колебания точек шнура 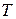 ; б) скорость распространения волны
; б) скорость распространения волны  ; в) длину волны
; в) длину волны  ; г) разность фаз колебаний
; г) разность фаз колебаний  точек шнура, находящихся на расстоянии
точек шнура, находящихся на расстоянии 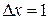 м; д) амплитуду скорости
м; д) амплитуду скорости  поперечного движения частиц шнура.
поперечного движения частиц шнура.
Дано:
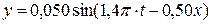 м м
 ,0 м ,0 м
| Решение Как известно, уравнение поперечной плоской волны, распространяющейся вдоль оси Х, имеет вид: |
а) 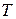 -?; б) -?; б)  –? в) –? в)  –?;
г) –?;
г)  –?; д) –?; д)  –? –?
|  , (1) , (1)
|
где  - амплитуда смещения,
- амплитуда смещения,  – циклическая частота,
– циклическая частота,  – волновое число,
– волновое число,  – начальная фаза. Из сравнения условий задачи и выражения (1) можно найти искомые величины.
– начальная фаза. Из сравнения условий задачи и выражения (1) можно найти искомые величины.
Период колебания  вязан с циклической частотой соотношением:
вязан с циклической частотой соотношением:
 . Поэтому
. Поэтому  с.
с.
Волновое число определяется выражением  .
.
Поэтому для скорости распространения волны  имеем
имеем

По найденным значениям периода колебаний  и скорости волны
и скорости волны  можно определить длину волны из соотношения
можно определить длину волны из соотношения  м.
м.
Разность фаз колебаний любых двух точек шнура определяется формулой
 .
.
Поэтому для точек шнура из условия задачи имеем
 рад.
рад.
Скорость смещения точек шнура в поперечном направлении получается дифференцированием по времени выражения (1), т.е.
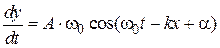 (2)
(2)
Из условия задачи и формулы (2) для максимального значения скорости  получается:
получается: 
Ответ: а)  с; б)
с; б)  м/с; в)
м/с; в)  м; г)
м; г) 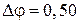 рад; д)
рад; д)  м/с.
м/с.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Найти смещение от положения равновесия точки, отстоящей от источника колебаний на расстояние l = l/12, для момента времени t = T /6. Амплитуда колебания А = 0,050 м.
(0,043 м)
2. Амплитуда гармонического колебания 5,0 см, период 4,0 с. Найти максимальную скорость колеблющейся точки и ее максимальное ускорение.
( = 7,8·10-2 м/с; am = 0,12 м/с2)
= 7,8·10-2 м/с; am = 0,12 м/с2)
4. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых х =A1sinw1 t и y = A2cosw2 t, где A1 = 8 cm, A2 = 4 см, w1 = w2 = 2 с--1. Написать уравнение траектории и построить ее.
5. Точка совершает простые гармонические колебания, уравнение которых x = Asinw t, где A=5 см, w= 2 с--1. В момент времени, когда точка обладала потенциальной энергией П = 0,1 мДж, на нее действовала возвращающая сила F=5 мН. Найти этот момент времени t.
6. Определить частоту n простых гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.
7. Определить период Т простых гармонических колебаний диска радиусом R == 40 см около горизонтальной оси, проходящей через образующую диска.
8. Определить период Т колебаний математического маятника, если его модуль максимального перемещения D r =18 см и максимальная скорость v max=16 см/с.
9. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение x о= 4 см, а скорость v о=10 см/с. Определить амплитуду А и начальную фазу jо колебаний, если их период T=2 с.
10. Складываются два колебания одинакового направления и одинакового периода: х1 = А 1sinw1 t и x 2= = A 2sinw2(t + t), где А 1 = А 2 = 3 см, w1 = w2 = pс--1, t = 0,5 с. Определить амплитуду А и начальную фазу jо результирующего колебания. Написать его уравнение. Построить векторную диаграмму для момента времени t = 0.
11. На гладком горизонтальном столе лежит шар массой М = 200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k = 500 Н/м. В шар попадает пуля массой m = 10 г, летящая со скоростью v = 300 м/с, и застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период T колебаний шара.
12. Шарик массой m = 60 г колеблется с периодом T=2 с. В начальный момент времени смещение шарика xо = 4,0 см и он обладает энергией E = 0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возвращающей силы с течением времени.
13. Уравнение плоской волны имеет вид y = 0,34×cos(0,20 t – 0,40 x), где y – смещение частиц среды, и все числовые значения заданы в системе СИ. Записать числовые значения частоты и периода колебаний, волнового числа, фазовой скорости и длины волны, а также максимальное значение смещения.
( = 0,50 м/с; l = 16 м)
= 0,50 м/с; l = 16 м)
14. Поперечная волна распространяется вдоль упругого шнура со скоростью  = 15 м/с. Период колебания точек шнура Т = 1,2 с. Определить разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях x 1 = 20 м, x 2 = 30 м. (200°)
= 15 м/с. Период колебания точек шнура Т = 1,2 с. Определить разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях x 1 = 20 м, x 2 = 30 м. (200°)
15. Материальная точка совершает гармонические колебания согласно уравнению  м. Определить: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу; 4) максимальную скорость точки; 5) максимальное ускорение; 6) через сколько времени после начала отсчета точка будет проходить положение равновесия.
м. Определить: 1) амплитуду колебаний; 2) период колебаний; 3) начальную фазу; 4) максимальную скорость точки; 5) максимальное ускорение; 6) через сколько времени после начала отсчета точка будет проходить положение равновесия.
(Т = 2 с;  м/c;
м/c; 

 )
)
16. Период затухающих колебаний Т = 4,0 с; логарифмический декремент затухания  начальная фаза
начальная фаза  При t = T /8 смещение точки х = 4,5 см. Написать уравнение этого колебания. Построить график этого колебания в пределах двух периодов.
При t = T /8 смещение точки х = 4,5 см. Написать уравнение этого колебания. Построить график этого колебания в пределах двух периодов.
( см)
см)
17. Поперечная волна, распространяясь вдоль упругого шнура, описывается уравнением  м. Определите: длину волны, фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии
м. Определите: длину волны, фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии  = 9 м от источника колебаний в момент времени
= 9 м от источника колебаний в момент времени  (
(



 )
)






