Модели сложных систем иерархического типа формируются в соответствии с принципом модульности, заключающимся в том, что моделирование химико-технологических систем основано на относительной самостоятельности и независимости их подсистем, допускающих декомпозицию анализируемой системы на составляющие ее подсистемы и формирование их моделей.
В соответствии с принципом модульности моделирования сложных систем модель подсистемы каждого уровня иерархии формируется как объединение моделей нижележащего уровня, а процесс взаимодействия подсистем взаимодействующих уровней моделируется с использованием координирующего соотношения. На рисунке 4 представлена иерархическая структура моделей ГХТС.

Рис. 4 Иерархическая структура моделей гибких ХТС.
Согласно классическому модульному принципу моделирование сложных систем, предполагает формирование моделей подсистем каждого уровня иерархии как объединение модулей нижележащих уровней. Обобщенная модель гибкой ХТС должна включать в себя модели отдельных аппаратов и дополнительные условия, определяющие функционирования ХТС как целостной системы.
В свою очередь, модель аппарата представляется как совокупность моделей отдельных операций и координирующих условий.
Модель каждой операции – это система уравнений, описывающих множество физико-химических процессов, протекающих в системе в пределах каждой элементарной операции. Модель произвольного уровня Lj иерархии является объединением моделей Mi нижележащего уровня Lj-1 и пересечением с координирующим соотношением Cj-1,j:
 , ,
| (1) |
где I - число моделей нижележащего уровня иерархии.
Элементом гибкой ХТС является технологический аппарат периодического, непрерывного или полунепрерывного действия. Технологическая стадия в АПД есть упорядоченная последовательность технологических операций, каждая из которых представляет собой совокупность типовых физико-химических процессов.
Графически структуру модели технологической операции можно представить следующим образом (рис.5).

Рис. 5. Структурное представление модели технологической операции.
Здесь: Mk- модель технологической операции k;
M1k- уравнения гидродинамики;
M2k- уравнения теплопередачи;
M3k- уравнения массопередачи;
M4k- уравнения химической кинетики.
Таким образом, модель Mk технологической операции k есть замкнутая система уравнений типовых процессов, что можно записать:
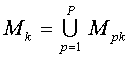 ; k=1,…,К ; k=1,…,К
| (2) |
где Mpk – уравнение типового процесса р (гидродинамического, теплового, диффузионного, химического);
Р – число процессов, образующих данную технологическую операцию;
К – число технологических операций, образующих цикл АПД.
Модель любой типовой технологической операции – это система дифференциальных и алгебраических уравнений с заданными начальными условиями, которые описывают гидродинамику, теплопередачу, массопередачу, химическую кинетику.

| (3) |
где y = {y1, y2,… yN }; x = {x1, x2,…,xN} – векторы зависимых переменных
τ – время
f, g – известные векторные функции
Например, математическая модель химической реакции в аппарате периодического действия (АПД) имеет вид системы уравнений:

| (4) |
где Ci, i = 1…k – концентрация реагентов и продуктов реакции
k – число компонентов реакции
r – скорость реакции
∆H – тепловой эффект
T0 – температура теплоносителя (или хладоагента)
f0, fi(i = 1…k), F – известные функции
Из моделей технологических операций Mkj, имеющих конечную временную продолжительность и заканчивающихся некоторым состоянием аппарата, а также моделей μj процесса их смены (т.е. смены состояний) и отображения, ставящего в соответствие множеству операций множество их моделей, формируется модель Mj технологического аппарата j периодического действия:
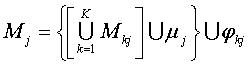 ; j = 1,…,J1; ; j = 1,…,J1; 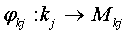 , ,
| (5) |
где J1 – число АПД.
Модели аппаратов непрерывного и полунепрерывного действия, которые могут входить в состав гибкой ХТС наряду с аппаратами периодического действия, совпадают с моделями реализуемых в них процессов, которые в этом случае могут рассматриваться как единственная операция бесконечной продолжительности в АПД или продолжительности, равной технологическому циклу в АПНД.
Для i-ой ХТС, образованной J1 аппаратами периодического действия, J2 – АНД и J3 – АПНД модель Mi ХТС формируется из моделей этих аппаратов Mj; j=1,…J, где  , моделей их взаимодействия υi и отображения ψi, ставящего в соответствие множеству технологических аппаратов множество их моделей. А т.к. работа технологических аппаратов в системе должна быть согласована по времени, то в обобщенной модели системы должна содержаться модель расписания работы составляющих ее аппаратов ρi:
, моделей их взаимодействия υi и отображения ψi, ставящего в соответствие множеству технологических аппаратов множество их моделей. А т.к. работа технологических аппаратов в системе должна быть согласована по времени, то в обобщенной модели системы должна содержаться модель расписания работы составляющих ее аппаратов ρi:
 , где i=1,…,I , где i=1,…,I
| (6) |
где  , I-число ХТС.
, I-число ХТС.
Здесь проявляется свойство эмерджентности системы, заключающееся в том, что модель системы не является простой совокупностью моделей образующих ее технологических аппаратов, а содержит также модели взаимодействия аппаратов, расписания их работы и отображения множества технологических аппаратов в множество их моделей. Таким образом, система приобретает новое качество, отсутствующее у отдельных аппаратов.
Гибкая ХТС многократно изменяет технологическую и организационную структуру, что обусловлено изменением номенклатуры и количества производимых ею продуктов; каждый раз, когда номенклатура и количество продуктов фиксируются, фиксируется и структура гибкой системы, которая в течение некоторого интервала времени, равного продолжительности производства продуктов этой номенклатуры, функционирует как индивидуальная или совмещенная с жесткой структурой.
Следовательно, модель гибкой системы Мι формируется из моделей Міι подсистем, на которые она декомпозируется при фиксации номенклатуры продукции. Модели подсистем дополняются моделями модификации ее технологической ζι и организационной χι структур и отображением ξι, ставящим в соответствие каждой индивидуальной (или совмещенной) системе іι ее модель Міι:

| (7) |
где 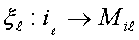 .
.
В общем случае существует не единственный способ организации технологических процессов в гибкой системе, а множество вариантов ее технологической структуры, поэтому Ml, ζl, χl и функция ξl являются переменными, как и число моделей






