множество является подмножеством самого себя.

Упражнения

1. Начертите три геометрические фигуры, принадлежащие объему понятия:

а) параллелограмм; б) трапеция; в) окружность.

2. Назовите пять существенных свойств понятия:

а) треугольник; б) круг.

3. Каков объем понятия:

а) однозначное число; б) натуральное число; в) луч?

4. Назовите несколько свойств, общих для прямоугольника и квадрата. Какое из следующих утверждений верное:

а) Всякое свойство квадрата присуще прямоугольнику.

б) Всякое свойство прямоугольника присуще квадрату?

5. Находятся ли в отношении рода и вида следующие па­ры понятий:

а) многоугольник и треугольник;

б) угол и острый угол;

в) луч и прямая;

г) ромб и квадрат;

д) круг и окружность?

6. Изобразите при помощи кругов Эйлера отношения меж­ду объемами понятий а, Ъ и с, если:

а) а - «четырехугольник», Ъ - «трапеция»,

с - «прямоугольник»;

б) а- «натуральное число, кратное 3»; Ъ - «натуральное число, кратное 4»; с - «натуральное число».

в) а - «треугольник»;

Ъ - «равнобедренный треугольник»; с - «равносторонний треугольник».

7. Приведите примеры понятий, от­ношения между объемами которых изображены на рисунке 30.

8. Среди понятий, изучаемых в на­чальном курсе математики, есть такие, как «четное число», «треугольник», «многоугольник», «число», «трехзнач­ное число», «прямой угол», «сумма», «слагаемое», «выражение». Есть ли среди них понятия, находящиеся в отношении:

а) рода и вида;

б) целого и части?

9. Какие свойства понятий «прямоугольник» и «сложение» изучают в начальном курсе математики?

14. Определение понятий

Появление в математике новых понятий, а значит, и но­вых терминов, обозначающих эти понятия, предполагает их определение.

Определением обычно называют предложение, разъясняющее суть нового термина (или обозначения). Как правило, делают
это на основе ранее введенных понятий. Например, прямо­угольник можно определить так: «Прямоугольником называ­ется четырехугольник, у которого все углы прямые». В этом определении есть две части - определяемое понятие (прямо­угольник) и определяющее понятие (четырехугольник, у кото­рого все углы прямые). Если обозначить через а первое поня­тие, а через b - второе, то данное определение можно предста­вить в таком виде:

а есть (по определению) Ъ.

Слова «есть (по определению)» обычно заменяют символом

, и тогда определение выглядит так:

on р.

а<=>Ь

on р.

Читают: «а равносильно b по определению». Можно про­читать эту запись еще и так: «а тогда и только тогда, когда Ь».

Определения, имеющие такую структуру, называются яв­ными. Сформулировать их можно по-разному. В математике используют определения через род и видовое отличие, генети­ческие, индуктивные и другие.

Примером определения через род и видовое отличие яв­ляется определение прямоугольника, данное выше. *В гене­тических определениях указывается способ образования определяемого объекта. Например, шар - это геометриче­ская фигура, получаемая в результате вращения полукруга вокруг диаметра. В индуктивных определениях указываются некоторые основные объекты теории и правила, позволяю­щие получать новые из уже имеющихся. Примером такого определения может служить определение арифметической прогрессии: «Арифметической прогрессией называется чи­словая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом».

Но чаще всего в математике используются определения че­рез род и видовое отличие. Рассмотрим подробнее структуру этих определений.

Обратимся опять к определению прямоугольника, вернее, к его второй части - определяющему понятию. В нем можно выделить:

1) понятие «четырехугольник», которое является родовым но отношению к понятию «прямоугольник»,

2) свойство «иметь все углы прямые», которое позволяет выделить из всевозможных четырехугольников один вид- прямоугольники; поэтому его называют видовым отличием.

Вообще видовое отличие - это свойства (одно или не­сколько), которые позволяют выделять определяемые объек­ты из объема родового понятия.

Итоги нашего анализа можно представить в виде схемы

Определяющее понятие

 

Заметим, что в наглядном представлении структуры опре­деления через род и видовое отличие мы допустили некоторые неточности. Во-первых, слова «родовое понятие» означают, что речь идет о родовом понятии по отношению к определяе­мому. Во-вторых, не совсем ясно, что означает знак «+», ко­торый, как известно, используется для обозначения сложения чисел. Смысл этого знака станет понятным немного позже, когда мы рассмотрим математический смысл союза «и». А пока познакомимся с еще одной возможностью наглядного представления определения через род и видовое отличие. Если определяемое понятие обозначить буквой а, определяющее буквой Ь, родовое понятие (по отношение к определяемому) - буквой с, а видовое отличие - буквой Р, то определение через род и видовое отличие можно представить так:

а<=>с+Р (2)

опр^

Почему видовое отличие обозначено заглавной буквой, мы узнаем несколько позже, в § 3.

Нам известно, что любое понятие имеет объем. Если поня­тие а определено через род и видовое отличие (2), то о его объеме - множестве Л - можно сказать, что в нем содержатся такие объекты, которые принадлежат множеству С (объему родового понятия с) и обладают свойством Р:

А = {х\хе СиР(х)}.

Например, если дано определение: «Острым углом называ­ется угол, который меньше прямого», - то объем понятия «острый угол» - это подмножество множества всех углов плос­кости, которые обладают свойством «быть меньше прямого».

Так как определение понятия через род и видовое отли­чие является по существу условным соглашением о введении нового термина для замены какой-либо совокупности из­вестных терминов, то об определении нельзя сказать, верное оно или неверное; его не доказывают и не опровергают. Но, формулируя определения, придерживаются ряда правил. Назовем основные.

1. Определение должно быть соразмерным. Это означает, что объемы определяемого и определяющего понятий должны совпадать. Это правило вытекает из того, что определяемое и определяющее понятия взаимозаменяемы.

Например, несоразмерно такое определение квадрата: «Квадратом называется четырехугольник, у которого все стороны равны». Действительно, объем определяемого по­нятия- множество квадратов. Объем определяющего поня­тия- множество четырехугольников, все стороны которых равны, а это множество ромбов. Но не всякий ромб есть квадрат, т.е. объемы определяемого и определяющего поня­тия не совпадают, и, следовательно, данное определение несоразмерно.

2. В определении (или их системе) не должно быть порочно­го круга. Это означает, что нельзя определять понятие через само себя (в определяющем не должно содержаться опреде­ляемого термина) или определять его через другое, которое, в свою очередь, определять через него.

Например, содержат порочный круг определения: «Рав­ные треугольники - это треугольники, которые равны», «Ка­сательная к окружности - это прямая, которая касается ок­ружности».

Так как в математике рассматривают не просто отдельные понятия, а их систему, то данное правило запрещает порочный круг и в системе определений. В соответствии с ним нельзя оп­ределять понятие а, выбрав в качестве родового понятия с, а понятие с - через понятие а.

Например, если определить окружность как границу кру­га, а круг как часть плоскости, ограниченную окружностью, то мы будем иметь порочный круг в определениях данных понятий.

3. Определение должно быть ясным. Это на первый взгляд очевидное правило, но означает оно многое. Прежде всего, требуется, чтобы значения терминов, входящих в определяю­щее понятие, были известны к моменту введения определения нового понятия.

Например, нельзя определять прямоугольник как паралле­лограмм с прямым углом, если понятие «параллелограмм» еще не рассмотрено.

К условиям ясности определения относят также требова­ния включать в видовое отличие лишь столько свойств, сколько необходимо и достаточно для выделения определяе­мых объектов из объема родового понятия.

Рассмотрим, например, такое определение прямоугольни­ка: «Прямоугольником называется четырехугольник, у кото­рого все углы прямые и противоположные стороны равны».

Нетрудно убедиться в том, что это определение соразмер­ное и в нем нет порочного круга. Но можно доказать, что свойство «в прямоугольнике противоположные стороны рав­ны» вытекает из свойства «в прямоугольнике все углы пря­мые». В этом случае считают, что в данном определении пря­моугольника второе свойство избыточное.

Таким образом, чтобы определение было ясным, жела­тельно, чтобы оно не содержало избыточных свойств в опре­деляющей части, т.е. таких свойств, которые могут быть вы­ведены из других, включенных в это определение. Однако иногда для простоты изложения это правило нарушают.

Для обеспечения ясности определения важно также налит чие понятия, родового по отношению к определяемому. Про­пуск родового понятия делает определение несоразмерным. Неприемлемо, например, такое определение квадрата: «Квад­рат - это когда все стороны равны».

К сказанному следует добавить, что, формулируя опреде­ление, надо стремиться в определяющем указывать не просто родовое по отношению к определяемому понятие, а ближай­шее. Это часто позволяет сократить количество свойств, включаемых в видовое отличие.

Например, если для определения квадрата в качестве родо­вого выбрать понятие «четырехугольник», то тогда надо бу­дет включать в видовое отличие два свойства: «иметь все прямые углы» и «иметь все равные стороны». В результате получим определение: «Квадратом называется четырехуголь­ник, у которого все углы прямые и все стороны равны».

Если же в качестве родового выбрать ближайшее для квадрата родовое понятие - прямоугольник, то получим более короткое определение квадрата: «Квадратом называется пря­моугольник, у которого все стороны равны».

4. Одно и то же понятие определить через род и видовое отличие, соблюдая сформулированные выше правила, можно по-разному. Так, квадрат можно определить как:

а) прямоугольник, у которого соседние стороны равны;

б) прямоугольник, у которого диагонали взаимно пер­пендикулярны;

в) ромб, у которого есть прямой угол;

г) параллелограмм, у которого все стороны равны, а уг­лы прямые.

Различные определения одного и того же понятия возмож­ны потому, что из большого числа свойств, входящих в со­держание понятия, в определение включаются только некото­рые. И когда из возможных определений выбирают одно, исходят из того, какое из них проще и целесообразнее для дальнейшего построения теории.

Если же одному и тому же понятию даются, например, два разных определения, то необходимо доказывать их равно­сильность, т.е. убеждаться в том, что из свойств, включенных в одно определение, вытекают свойства, включенные в другое, и наоборот.

Завершая рассмотрение определений понятий через род и видовое отличие, назовем ту последовательность действий, ко­торую мы должны соблюдать, если хотим воспроизвести опре­деление знакомого понятия или построить определение нового:

1. Назвать определяемое понятие (термин).

2. Указать ближайшее родовое (по отношению к опреде­ляемому) понятие.

3. Перечислить свойства, выделяющие определяемые объек­ты из объема родового, т.е. сформулировать видовое отличие.

4. Проверить, выполнены ли правила определения понятия (соразмерно ли оно, нет ли порочного круга и т.д.).

При изучении математики в начальных классах определения через род и видовое отличие используют редко. Связано это как с особенностями курса, так и с возможностями детей. Но поня­тий в начальном курсе математики очень много - об этом мы говорили в самом начале параграфа. Как же их определяют?

При изучении математики в начальной школе чаще всего используют так называемые неявные определения. Среди них различают контекстуальные и остенсивные.

В контекстуальных определениях содержание нового по­нятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающей смысл вво­димого понятия. Посредством контекста устанавливается

связь определяемого понятия с другими, известными, и тем самым косвенно раскрывается его содержание. Примером контекстуального определения может быть определение урав­нения и его решения, приведенное в учебнике математики для II класса (Моро М. И., Бантова М. А. Математика: Учеб. для 2 класса трехлетней начальной школы. - М.: Просвещение, 1987. - С. 196). Здесь после записи □ + 6 = 15 и перечня чисел О, 5, 9, 10 идет текст: «К какому числу надо прибавить 6, что­бы получилось 15? Обозначим неизвестное число латинской буквой х (икс):

х + 6 = 15 - это уравнение.

Решить уравнение - значит найти неизвестное число. В дан­ном уравнении неизвестное число равно 9, так как 9 + 6 = 15. Объясни, почему числа 0, 5 и 10 не подходят». Остенсивные определения - это определения путем показа. Они используются для введения терминов путем демонстра­ции объектов, которые этими терминами обозначают. На­пример, таким способом можно определить в начальной шко­ле понятия равенства и неравенства:

2-7 >2-6 9-3 = 27

78 - 9 < 78 6-4 = 4-6

37 + 6 > 37 17-5 = 8 + 4

Это неравенства. Это равенства. Остенсивные определения, как и контекстуальные, харак­теризуются некоторой незавершенностью. Действительно, определение посредством показа не выделяет числовые ра­венства (неравенства) из других предложений, в нем не ука­зываются свойства, характерные для данных понятий. Они только связывают термины с определяемыми объектами. Поэтому после контекстуального или остенсивного опреде­ления понятия необходимо дальнейшее изучение свойств так определенных объектов.

Упражнения

1. Покажите, что следующие определения имеют форму равносильности, и переформулируйте их, используя слова «тогда и только тогда, когда»:

а) Четным называется число, которое делится на 2.

б) Множество А называется подмножеством множества В, если каждый элемент множества А принадлежит множеству В.

в) Множества А и В называются равными, если А аВ и BczA.

г) Треугольником называется фигура, которая состоит их трех точек, не лежащих на одной прямой, и трех попарно со­единяющих их отрезков.

2. В следующих определениях выделите определяемое и

определяющее понятия, родовое понятие (по отношению к

определяемому) и видовое отличие:

а) Параллелограммом называется четырехугольник, у ко­торого противоположные стороны попарно параллельны.

б) Отрезок, соединяющий середины двух сторон треуголь­ника называется его средней линией.

3. Назовите все свойства, которые содержатся в видовом

отличии каждого из следующих определений:

а) Биссектрисой угла называется луч, выходящий из вер­шины угла и делящий угол пополам, а j к-Vci-O ' о

б) Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

4. Соразмерны ли следующие определения:

а) Остроугольным треугольником называется треугольник,

у которого острый угол.

б) Прямоугольным треугольником называется треуголь­ник, у которого есть прямой угол.

5. Учащийся определил прямой угол как угол, стороны ко­торого взаимно перпендикулярны, а взаимно перпендикуляр­ные прямые как прямые, образующие при пересечении пря­мые углы. Какую ошибку допустил учащийся?

6. Есть ли логические ошибки в следующих определениях?

Если можете, исправьте их.

а) Прямоугольником называется четырехугольник, у кото­рого противоположные стороны равны.

б) Биссектрисой угла называется прямая, делящая угол по­полам.

в) Сложением называется действие, при котором числа складываются.

г) Равносторонним треугольником называется треуголь­ник, у которого равны все стороны и все углы.

д) Параллелограммом называется многоугольник, у кото­рого противоположные стороны попарно параллельны.

7. Дайте определение: тупоугольного треугольника, рав­нобедренного треугольника, трапеции. Какие понятия вы выбрали в качестве родового в каждом случае? Какие свойст­ва включили в видовое отличие?

8. Сформулируйте определение прямоугольника, используя

в качестве родового понятия «четырехугольник». Пользуясь

 

Рис.31

9. Понятие «противоположные стороны прямоугольника» в начальном курсе математики можно определить так: «Крас­ным цветом обозначены две противоположные стороны пря­моугольника, а синим цветом - две другие противоположные стороны» (все это показано на рисунке).

Какой способ определения понятия использован?

10. Выясните, каким способом определяются в различных учебниках по математике для начальных классов понятия:

а) выражение; г) четное число;

б) сумма; д) однозначное число;

в) слагаемое; е) умножение.

15. Основные выводы § 2

Изучив материал этого параграфа, мы уточнили свои представления о математических понятиях:

- это понятия об идеальных объектах;

- каждое математическое понятие имеет название (термин), объем и содержание;

- математические понятия могут находиться в отношении рода и вида, если их объемы находятся в отношении включе­ния, но не совпадают;

- математические понятия могут быть тождественными, если их объемы совпадают;

- понятиям дают определения; они могут быть явными и неявными; к неявным относят контекстуальные и остенсивные определения; среди явных чаще всего используются определе­ния через род и видовое отличие;

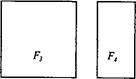
этим определением, объясните, почему фигуры Fh F3 и F4, изображенные на рисунке 31, можно назвать прямоугольни­ками, а фигуру F2 - нет.

- при воспроизведении или конструировании определений через род и видовое отличие необходимо соблюдать ряд пра­вил.: определение должно быть соразмерным, в нем не должно быть порочного круга, оно должно быть ясным. \

§3. МАТЕМАТИЧЕСКИЕ ПРЕДЛОЖЕНИЯ

Изучая реальные процессы, математика описывает их, ис­пользуя как естественный словесный язык, так и свой симво­лический. Описание строится при помощи предложений. Но чтобы математические знания были достоверными, правиль­но отражали окружающую нас реальность, эти предложения должны быть истинными.

Но как узнать, истинное или ложное знание заключено в том или ином математическом предложении? На этот и другие вопросы, с ним связанные, мы попытаемся ответить в данном параграфе. А сейчас только заметим, что каждое математиче­ское предложение характеризуется содержанием и логической формой (структурой), причем содержание неразрывно связано с формой, и нельзя осмыслить первое, не понимая второго. В связи с этим изучение математических предложений в главе «Элементы логики» будет в основном связано с раскрытием логической структуры математических предложений.

16. Высказывания и высказывательные формы

Относительно понятий и отношений между ними можно вы­сказывать различные суждения. Языковой формой суждений яв­ляются повествовательные предложения. Например, в началь­ном курсе математики можно встретить такие предложения:

1) число 12 - четное;

2) 2 + 5 > 8;

3) jc + 5 = 8;

4) В числе 15 один десяток и 5 единиц;

5) От перестановки множителей произведение не изменяется;

6) Некоторые числа делятся на 3.

Видим, что предложения, используемые в математике, могут быть записаны как на естественном (русском) языке, так и на математическом, с использованием символов. Далее, о предло­жениях 1, 4, 5 и 6 можно сказать, что они несут верную инфор­мацию, а предложение 2 - ложную. Относительно предложения v + 5 = 8 вообще нельзя сказать: истинное оно или ложное.

Взгляд на предложение с позиции - истину или ложь оно мам сообщает - привел к понятию высказывания.

Высказыванием в математике называют предложение, относительно которого имеет смысл вопрос: истинно оно или ложно.

Например, предложения 1, 2, 4, 5 и 6, приведенное¹ йыше, есть высказывания, причем предложения 1, 4, 5 и 6 - истин­ные, а 2 - ложное.

Высказывания принято обозначать прописными буквами латинского алфавита: А, В, С, Z. Если высказывание А истинно, то записывают: А - «и», если же высказывание А - ложно, то пишут: А - «л».

«Истина» и «ложь» называются значениями истинности высказывания. Каждое высказывание либо истинно, либо лож- ⁱ но, быть одновременно тем и другим оно не может.

Предложение л: + 5 = 8 не является высказыванием, так как о нем нельзя сказать: истинно оно или ложно. Однако при подстановке конкретных значений переменной х оно обращается в высказывание: истинное или ложное. Напри­мер, если х = 2, то 2 + 5 = 8 - ложное высказывание, а при х = 3 оно обращается в истинное высказывание 3 + 5 = 8. Предложение х + 5 = 8 называется высказывательной фор­мой. Оно порождает множество высказываний одной и той же формы.

По числу переменных, входящих в высказывательную фор­му, различают одноместные, двухместные и т.д. высказыва- тельные формы и обозначают: А{х), А{х, у) и т.д. Например, х + 5 = 8 - одноместная высказывательная форма, а предло­жение «Прямая х параллельна прямой у» - двухместная.

Следует иметь в виду, что в высказывательной форме пе­ременные могут содержаться неявно. Например, в предложе­ниях: «число четное», «две прямые пересекаются» переменных нет, но они подразумеваются: «Число х - четное», «Две пря­мые х и у пересекаются».

Задание высказывательной формы, как правило, предпо­лагает и задание того множества, из которого выбираются значения переменной (переменных), входящей в высказыва­тельную форму. Это множество называется областью опре­деления высказывательной формы. Например, неравенство х> 5 можно рассматривать на множестве натуральных чи­сел, а можно считать, что значение переменной х выбирает­ся из множества действительных чисел. Тогда в первом слу­чае областью определения неравенства х > 5 будет множест­во натуральных чисел, а во втором множество действитель­ных чисел.

Дадим определение одноместной высказывательной фор­мы (понятие высказывательной формы, содержащей две и более переменных, определяется аналогично).

Определение. Одноместной высказывательной формой, заданной на множестве X, называется предложение с пе­ременной, которое обращается в высказывание при под­становке в него значений переменной из множества X. Среди всех возможных значений переменной нас в пер­вую очередь интересуют те, которые обращают высказыва- тельную форму в истинное высказывание. Множество таких значений переменных называют множеством истинности высказывательной формы. Например, множеством истинно­сти высказывательной формы * > 5, заданной на множестве действительных чисел, будет промежуток (5; °о). Множество истинности высказывательной формы х + 5 = 8, заданной на множестве целых неотрицательных чисел, состоит из одного числа 3.

Условимся обозначить множество истинности высказы­вательной формы буквой Т. Тогда, согласно определению, всегда ТаХ.

Предложения (высказывания и высказывательные формы), которые мы рассматривали, были простыми, но можно при­вести примеры суждений, языковой формой которых будут сложные предложения. Например: «Если треугольник равно­бедренный, то углы при основании в нем равны». Естественно возникает вопрос: как определить значение истинности таких высказываний и находить множество истинности таких вы- сказывательных форм?

Чтобы ответить на эти вопросы, необходимо познако­миться с некоторыми логическими понятиями.

В логике считают, что из двух данных предложений можно образовать новые предложения, используя для этого союзы «и», «или», «если..., то...», «тогда и только тогда, когда» и др. С помощью частицы «не» или словосочетания «неверно, что» уожно из одного предложения получить новое.

Слова «и», «или», «если..., то...», «тогда и только тогда, / когда», а также частицу «не» (слова «неверно, что») называют I логическим связками.Предложения, образованные из других предложений с йомощью логических связок, называют со­ставными. Предложения, не являющиеся составными, назы- I вают элементарными.

\ Приведем примеры составных предложений: 1) Число 28 четное и делится на 7.

Это предложение образовано из двух элементарных: «число 28 четное», «число 28 делится на 7» с помощью логиче­ской связки «и».

2) Число х меньше или равно 8.

%Это предложение образовано из двух элементарных: «чис­ло х меньше 8», «число х равно 8» с помощью логической связки «или».

3) Число 14 не делится на 4.

Это составное высказывание образовано из предложения «число 14 делится на 4» с помощью частицы «не».

Вы, наверное, уже обратили внимание на то, что все три предложения, являясь с логической точки зрения составными, по своей грамматической структуре - простые. Не всегда, но так бывает: простое предложение по своей логической струк­туре может быть составным.

А как определять значение истинности составного выска­зывания? Например, истинно или ложно высказывание: «число 28 делится на 7 и на 9»? Элементарное высказывание «число 28 делится на 7», входящее в составное, истинное - это известно из начального курса математики. Второе эле­ментарное высказывание «число 28 делится на 9» - ложное (и это нам известно). А каким будет в этом случае значение истинности составного высказывания, образованного из этих высказываний с помощью союза «и»? Ответить на этот вопрос можно, если знать смысл этого союза. Но так как составные высказывания образуются с помощью и других логических связок, то возникает необходимость в уточнении их смысла.

Кроме того, уточнение смысла используемых в математике связок обусловлено их неоднозначным толкованием в обы­денной речи, что может привести к неоднозначному ответу при нахождении значения истинности составных высказываний.

Итак, значение истинности элементарного высказывания определяют, исходя из его содержания с опорой на известные знания. Чтобы определить значение истинности составного высказывания, надо знать смысл логических связок, с помо­щью которых оно образовано из элементарных, и уметь вы­являть логическую структуру высказывания.

Для выявления логической структуры составного предло­жения нужно установить:

1) из каких элементарных предложений образовано данное составное предложение;

2) с помощью каких логических связок оно образовано.

Выявим, например, логическую структуру предложения

«Если углы вертикальные, то они равны». Оно состоит из двух элементарных предложений: предложения А - «углы вер­тикальные» и предложения В - «углы равнял». Соединены они в одно составное предложение с помощью логической связки «если то...». Говорят, что данное составное предложение имеет логическую структуру (форму): «если А, то В».

Упражнения

1. Среди следующих предложений, рассматриваемых в на­чальном курсе математики, укажите высказывания и опреде­лите их значение истинности:

а) (12-7) (6 + 3) = 45;

б) (15+ 12): 3> 10;

в) в любом прямоугольнике противоположные стороны равны;

г) (12-х) • 4 = 24;

д) среди четырехугольников есть такие, у которых все сто­роны равны;

е) число z - двузначное;

ж) произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174;

з) число 6 является корнем уравнения (12 - х) • 4 = 24.

2. Какие предложения из упражнения 1 являются высказы- вательными формами? Подставьте в них значение переменной так, чтобы получилось:

а) истинное высказывание; б) ложное высказывание.

3. Можно ли считать высказывательными формами сле­дующие записи:

а) х²- 2х; в) 7-4+ 2 = 30;

б) Ах + 2у; г) 7-4 + 2 < 30?

4. Найдите множество истинности высказывательной фор­мы 2х - 10 < 0, заданной на множестве X, если

a)X=R; 6)X = N в)Х= {0, 1,2,3,4,5,6,7}.

5. Изобразите на координатной прямой множество истин­ности каждого из предложений при условии, что все они за­даны на множестве R:

а) * > 2; в) 2 < х < 6; д) 2 < х < 6;

б) х < 3; г) 2 <х < 6; е)2<х<6.

Как можно записать, используя общепринятые символы, множество истинности каждого из данных предложений?

6. Изобразите на координатной плоскости множества истинности следующих предложений при условии, что х, у е R:

а) х = у; в) х = 2; д) у = 2х + 3;

б) у = 2х; г) >> = 2; е)>> = 2х-3.

7. В следующих составных предложениях выделите состав­ляющие их элементарные предложения и логические связки:

а) В равнобедренном треугольнике ЛВС биссектриса BD является медианой и высотой.

б) х > 7.

в) Если запись числа оканчивается цифрой 0, то число де­лится на 5.

г) Треугольник является равносторонним тогда и только тогда, когда все его углы равны.

д) Неверно, что число 17 делится на 3.

е) Если а-Ъ = 0, то а - 0 или b = 0.

8. Какова логическая структура (форма) следующих пред­ложений:

а) Средняя линия треугольника параллельна основанию и равна его половине.

б) Если число делится на 2 и на 3, то оно делится на 6.

в) Треугольник ЛВС не является равносторонним.

9. Приведите примеры математических предложений, имею­щих логическую структуру вида:

г)АиВ', б),4 или 2?; в) если А, то В.

10. Покажите, что выполнение учащимися начальных клас­сов следующих заданий связано с понятием высказывательной формы, области ее определения и множества истинности:

а) Из ряда чисел 1, 2, 3, 4, 5, 6, 7, 8, 9 выпиши те, которые делятся на 3.

б) Назови все числа, меньшие 7 (имеются в виду только це­лые неотрицательные числа).

17. Конъюнкция и дизъюнкция высказываний ^[1]

Выясним смысл, который имеет в математике союз «и». Пусть А и В - произвольные высказывания. Образуем из них, с помощью союза «и», составное высказывание. Назовем его конъюнкцией и обозначим А д В (читают: «А и В»).

/Определение. Конъюнкцией высказываний А и В называет-

/ ся высказывание А л В, которое истинно, когда оба выска-

\ зывания истинны, и ложно, когда хотя бы одно из этих

\высказываний ложно.

Определение конъюнкции можно записать с помощью таблицы, называемой таблицей истинности.

А	В	АлВ
и	и	и
и	л	д
л	и	л
л	л	л

 

Используя данное определение, найдем значение истинно­сти высказывания «число 28 делится на 7 и на 9», которое, как было установлено раньше, состоит из двух элементарных высказываний, соединенных союзом «и», т.е. является конъ­юнкцией. Так как первое высказывание истинно, а второе ложно, то, согласно определению конъюнкции, высказывание «число 28 делится на 7 и на 9» будет ложным.

Заметим, что данное определение конъюнкции не расхо­дится с общепринятым пониманием союза «и». Действитель­но, если мы знаем, что каждое из предложений «сегодня идет снег» и «сегодня холодно» истинно, то мы будем считать ис­тинным и предложение «сегодня идет снег и холодно». Если же одно из этих предложений или оба будут ложными, то и все предложение «сегодня идет снег и холодно» мы будем счи­тать ложным.

Заметим также, что в обыденной речи конъюнкция может выражаться не только с помощью союза «и», но и другими, например, «а», «но», «однако», «не только..., но и...». Напри­мер: «Число 15 делится не только на 3, но и на 5».

Выясним теперь, какой смысл имеет в математике союз «или».

Пусть А и В - произвольные высказывания. Образуем из них с помощью союза «или» составное высказывание. Назо­вем его дизъюнкцией и обозначим A v В (читают: «А или В»). Определение. Дизъюнкцией высказываний А и В называет­ся высказывание A v В, которое истинно, когда истинно хотя бы одно из этих высказываний, и ложно, когда оба высказывания ложны.

Таблица истинности дизъюнкции имеет вид:

А	В	AvB
и	и	и
и	л	и
л	и	и
л	л	л

 

Используя данное определение, найдем значение истинности нысказывания «число 28 делится на 7 или на 9». Так как это
предложение является дизъюнкцией двух высказываний, одно из которых истинно, то, согласно определению, оно истинно.

Из определения дизъюнкции следует, что в математике союз «или» используется как неразделительный, т.е. допус­кается возможность одновременного выполнения обоих условий. Так, высказывание «15 кратно 3 или 5», согласно определению, считается истинным, поскольку оба высказы­вания «15 кратно 3» и «15 кратно 5» истинны.

Образование составного высказывания с помощью логи­ческой связки называется логической операцией. Операция, соответствующая союзу «и», называется конъюнкцией, опера­ция, соответствующая союзу «или», - дизъюнкцией. Заметим, что названия логических операций и их результаты (состав­ные предложения) называются одинаково.

Определения конъюнкции и дизъюнкции можно обобщить на г составляющих их высказываний.

Конъюнкцией t высказываний называется предложение ви­да Aj л А₂ а ... л A_t, которое истинно тогда и только тогда, когда истинны все составляющие его высказывания.

Дизъюнкцией t высказываний называется предложение ви­да Aj v А₂ v... v А,, которое ложно тогда и только тогда, когда ложны все составляющие его высказывания.

Упражнения

1. Известно, что высказывание А истинно. Можно ли, зная лишь это, определить значение истинности высказывания:

а)АлВ; б)AvBl

2. Известно, что высказывание А - ложно. Можно ли, зная лишь это, определить значение истинности высказывания:

а)АлВ; 6)AvBl

3. Определите значение истинности ка­ждого высказывания:

а) число 6 делится на 2 и на 3;

б) число 123 делится на 3 и на 9;

в) при делении 42 на 5 в остатке получится 2 или 5;

г) треугольник ABC (рис. 32) пря­моугольный и равносторонний;

д) один из углов треугольника ABC (рис. 32) равен 60°.

е) 3 < 7; Ж) 3 > 7. Рис.32

4. Каждое из следующих предложений замените конъюнк­цией либо дизъюнкцией, имеющей тот же смысл:

а) число 7 принадлежит хотя бы одному из множеств А и Z?;

б) квадратное уравнение имеет не более двух корней;

в) каждое слагаемое суммы х + у + z делится на 3;

г) по крайней мере одно из натуральных чисел п, п-1, п + 1 четно.

5. А - множество четных натуральных чисел, В - множест­во натуральных чисел, меньших 20. Установите, какие из сле­дующих высказываний истинны:

а) 5 € А или 5 е В; д) 44 е А или 44 е В;

б)5 е А и 5 е В; е) 44 е А и 44 е В\

в) 8 е А или 8 € В; ж) 51 е А или 51 е В;

г) 8 е и 8 е з)51еЛи51еЯ.

18. Конъюнкция и дизъюнкция высказывательных форм

В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствую­щие операции над высказывательными формами.

Конъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве X, обозначают А(х) л В(х). С появлением этого предложения возникает вопрос, как найти его множество истинности, зная множества истинности вы­сказывательных форм А(х) и В(х). Другими словами, при ка­ких значениях х из области определения X высказывательная форма А(х) л В(х) обращается в истинное высказывание? Оче­видно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе вы- сказывательные формы А(х) и В(х). Если обозначить Т_А- множество истинности предложения А(х), Т_в- множество истинности предложения В(х), а множество истинности их конъюнкции Т_АлВ, то, по всей видимости, Т_АлВ = Т_Ап Т_в.

Докажем это равенство.

1. Пусть а - произвольный элемент множества X и извест­но, что a g Т_АлВ. По определению множества истинности это означает, что высказывательная форма А(х) л В(х) обращает­ся в истинное высказывание при х = а, т.е. высказывание А (я) д 5(a) истинно. Так как данное высказывание конъюнк­ция, то, по определению конъюнкции, получаем, что каждое и*1 высказываний А (а) и В (а) также истинно. Это означает, что а е Т_А и а е Т_в. Следовательно, по определению пересече-

\ II. II. Стойлова.

ния множеств, ае Т_Аг\ Т_в. Таким образом, мы показали, что Т_Алвс^п Т_в.

2. Докажем обратное утверждение. Пусть а- произволь­ный элемент множества X и известно, что а е Т_А п Т_в. По определению пересечения множеств это означает, что а е Т_А и а е Т_в, откуда получаем, что А{а) и В(а) - истинные высказы­вания, поэтому конъюнкция высказываний А(а)лВ(а) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х)лВ(х), т.е. а е Т_АлВ. Таким образом, мы доказали, что Т_А п Т_в с Т_АЛВ.

Из 1 и 2 в силу определения равных множеств вытекает справедливость равенства Т_АлВ = Т_А п что и требовалось доказать.

Заметим, что полученное правило справедливо и для вы­сказывательных форм, содержащих более одной переменной.

Приведем пример использования этого правила. Найдем множество истинности конъюнкции двух неравенств 2х > 10 и 4 + х < 12, т.е. множество истинности предложения 2х> 10 л 4 + л; < 12. Пусть Tj- множество решений неравенст­ва 2х > 10, а Т₂ - множество решений неравенства 4 + х < 12. Тогда Г; = (5, +«*>), Т₂ = (—о°, 8). Чтобы найти те значения х, при которых истинны оба неравенства, надо найти пересе­чение их множеств решений: Г₇ п Т₂ = (5, 8).

Видим, что выполнение этого задания свелось к решению системы неравенств. Вообще с точки зрения логики любая система неравенств есть конъюнкция неравенств, так же как и система уравнений есть конъюнкция уравнений.

Дизъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве X, обозначают A(x)vB(x). Это предложение будет обращаться в истинное высказывание при тех и только тех значениях х из области определения X, при которых обращается в истинное высказывание хотя бы одна из высказывательных форм, т.е. T_AsfB -T_a\j Т_в..

Доказательство этого равенства проводится аналогично рассмотренному выше.

Приведем пример использования этого правила. Решим, на­пример, уравнение (х - 2) (х + 5) = 0. Известно, что произведе­ние равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Это означает, что дацное уравнение равносильно дизъюнкции: x-2 = 0vx + 5 = 0h поэтому множе­ство его решений может быть найдено как объединение множеств решений первого и второго уравнений, т.е. {2} и {-5} = {-5, 2}.

Заметим, что дизъюнкцию уравнений (неравенств) назы­вают также совокупностью. Решить совокупность уравнений (неравенств) - это значит найти те значения переменных, при которых истинно хотя бы одно из уравнений (неравенств), входящих в нее.

Рассматривая конъюнкцию и дизъюнкцию высказыватель- ных форм, мы установили их тесную связь с пересечением и объединением множеств.

С другой стороны, характеристические свойства элементов пересечения и объединения множеств А и В представляют собой соответственно конъюнкцию и дизъюнкцию характери­стических свойств данных множеств:

А сл В = {х\х е А их е В), А и В = {х\х е А или х е В}, причем каждое свойство представляет собой высказыватель- ную форму.

Упражнения

1. Покажите, что, выполняя следующие задания, мы нахо­дим множество истинности конъюнкции и дизъюнкции вы- сказывательных форм:

а) Даны числа: 31, 53, 409, 348, 20, 3094, 233, 33, 271, 143, 3, 333,14, 30. Выпишите все числа, в записи которых:

1) три цифры и есть цифра 3;

2) три цифры или есть цифра 3.

б) Из ряда 25, 12, 17, 5, 15, 36 выпишите числа:

1)двузначные или меньшие 17;

2) двузначные и меньшие 17.

в) Из ряда 72,312,522,483,1137 выпишите те числа, которые:

1)делятся на 3 и 9;

2) делятся на З^ли на 9.

2. Выполните следующие задания и дайте им теоретико- множественное обоснование:

а) Постройте по два треугольника, принадлежащих множе­ству А, если оно состоит из:

прямоугольных и равнобедренных треугольников;

прямоугольных или равнобедренных треугольников.

б) Постройте два четырехугольника, у которых:

1)диагонали равны и есть прямой угол;

2) диагонали равны или есть прямой угол.

в) Запищите три числа, которые:

1)делятся на 4 и больше 12;

2) делятся на 4 или больше 12.

3. Решите следующие системы неравенств и объясните, что представляет собой любая система неравенств и множество ее решений с точки зрения логики:

ГЗх — 5 > 10; f4x + 3< 11;

\х + 8<2х; [Зх-7>8.

4. Решите уравнение (х - 3)-(х + 2) (х - 7) = 0, х е R. Ис­пользовалось ли вами понятие дизъюнкции высказыватель- ных форм?

5. Вместо многоточия вставьте «и» либо «или»:

а)хе А пВ тогда и только тогда, когда х е А... х е В.

б) хе А и В тогда и только тогда, когда л: е А... д: g В.

6. Пусть А - множество ромбов, В - множество прямоуголь­ников. Как называется четырехугольник, являющийся одно­временно ромбом и прямоугольником? Как можно выразить множество К таких четырехугольников через множества А и В!

19. Решение задач на распознавание объектов

С введением понятия конъюнкции и дизъюнкции высказы- вательных форм появились условия для рассмотрения вопро­сов, связанных с решением определенного вида задач, так называемых задач на распознавание объектов.

В задачах на распознавание требуется ответить на вопрос: принадлежит тот или иной объект объему данного понятия или не принадлежит. Примером такой задачи может быть следующая: «Установите, какие из фигур на рисунке 33 явля­ются квадратами, а какие нет».

Рис. 33

 

Решают такие задачи, используя определение соответст­вующего понятия. При этом важно понимать, что если поня­тие а определено через родовое понятие с и видовое отличие Р, то его объем А можно представить в таком виде: А = {х | х е С и Эта запись показывает, что характеристическое свой­ство элементов, принадлежащих объему понятия а, представ­ляет собой конъюнкцию двух свойств:

1) принадлежности объекта х объему С родового понятия (х е Q;

2) свойства Р(х).

Это означает, что объект х будет принадлежать объему понятия а тогда и только тогда, когда он (этот объект) содер­жится в объеме родового понятия и обладает свойством Р. Поэтому распознавание производится по следующему правилу:

1. Проверяем, принадлежит ли объект х объему родового понятия, т.е. истинно ли высказывание х е С.

2. Если окажется, что х е С, то проверку прекращаем и де­лаем вывод, что объект х не принадлежит объему понятия а, т.е. х е Л.

3. Если х е С, то продолжаем проверку и выясняем, обла­дает ли объект х свойством Р.

4. Если объект х обладает свойством Р, то делаем вывод о его принадлежности объему понятия а, т.е. утверждаем, что хеЛ.

5. Если окажется, что объект х не обладает свойством Р, то делаем вывод, что объект х не принадлежит объему понятия а, т х.хеА.

Выясним, например, какие из фигур на рисунке 33 являются квадратами. Будем пользоваться таким определением: «Квад­ратом называется прямоугольник, у которого соседние стороны равны». Из него следует, что для того, чтобы фигура была квадратом, она должна обладать двумя свойствами: «быть прямоугольником» и «иметь равные соседние стороны».

Фигура 1 является квадратом, так как это прямоугольник, соседние стороны которого равны.

Фигура 2 не является квадратом, так как это не прямо­угольник.

Фигура 3 - прямоугольник, но соседние стороны в нем не равны. Следовательно, ее нельзя назвать квадратом.

Мы рассмотрели самый простой случай решения задачи на распознавание, когда видовое отличие в определении понятия состояло только из одного свойства. Но нередки и такие оп­ределения, в которых видовое отличие состоит из нескольких свойств, связанных между собой союзами «и», «или».

Если видовое отличие представляет собой конъюнкцию свойств, т.е. Р = Pj д Р₂ д... д Р_п, то распознавание проводит­ся по следующему правилу: проверяют поочередно наличие у Объекта каждого из свойств Р₇, Р₂, Р_п\ если окажется, что
он не обладает каким-либо из этих свойств, то проверку пре­кращают и делают вывод о том, что объект не обладает свой­ством Р; если же окажется, что все свойства Р_ь Р₂,..., Р_п при­сущи данному объекту, то заключают, что объект обладает свойством Р.

Выясним, например, в каком случае луч BD является бис­сектрисой угла ABC (рис. 34). Воспользуемся таким определе­нием биссектрисы угла: «Биссектрисой угла называется луч, выходящий из вершины угла и делящий этот угол пополам». Из него следует, что для того, чтобы луч был биссектрисой угла, он должен обладать двумя свойствами: «выходить из вершины угла» и «делить этот угол пополам».

 

Рис.34

Луч BD на рисунке 34а не является биссектрисой угла ABC, поскольку он не делит данный угол пополам.

Луч BD на рисунке 346 биссектриса угла ABC, так как он выходит из вершины этого угла и делит его пополам.

Если видовое отличие представляет собой дизъюнкцию свойств Р = Pj v Р₂ v... v Р_п, проверка проводится до тех пор, пока не будет установлено, что хотя бы одно из свойств при­суще данному объекту, на основании чего заключают, что он обладает свойством Р. Если же окажется, что объект не обла­дает ни одним из свойств Pj, Р₂,..., Р_п, то приходят к выводу, что он не обладает свойством Р.

Упражнения

1. Дайте определение квадрата через понятие «прямоуголь­ник». Пользуясь данным определением, укажите условия, при которых фигура:

а) будет являться квадратом;

б) не будет являться квадратом.

2. Выявите логическую структуру следующих определений:

а) Параллельные прямые- это две прямые, принадлежа­щие плоскости и непересекающиеся или совпадающие.

б) Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

3. Установите, в каком из случаев (рис. 35) отрезок PQ яв­ляется диаметром круга. Каким определением диаметра удоб­нее воспользоваться при решении данной задачи:

а) Диаметр круга - это хорда, проходящая через его центр.

б) Диаметр круга - это отрезок, соединяющий две точки ок­ружности и проходящий через центр.

Рис.35

 

4. Установите, в каком из рассматриваемых случаев отре­зок MP будет средней линией треугольника ABC (рис. 36).

Рис.36

 

5. Каким образом вы будете решать следующие задачи, предлагаемые младшим школьникам:

а) Найди среди записей уравнения и реши их устно: 8 + 7=15, 17-* = 9, 17-х, х + 12 = 12.

б) Назови уравнения, в которых неизвестное число равно 8: х-2 = 20; 6-х = 48; х:2 = 5; 40:х = 5.

20. Высказывания с кванторами

В параграфе, который мы изучаем, рассматриваются раз­личные виды математических предложений. Мы выяснили, что среди них выделяют высказывания и высказывательные формы, которые могут быть элементарными и составными. Мы узнали также, как устанавливают значение истинности таких высказываний и как находят множество истинности высказывательных форм. Но мы, конечно, не исчерпали все многообразие формулировок математических предложений и, значит, не знаем многих правил обращения с ними. Напри­мер, почему можно одну и ту же теорему о равенстве верти­кальных углов формулировать по-разному:

1) Вертикальные углы равны.

2) Если углы вертикальные, то они равны.

3) Для того чтобы углы были равны, достаточно, чтобы они были вертикальными.

4) Для того чтобы углы были вертикальными, необходимо, чтобы они были равны.

Или: почему истинность предложения «сумма трех любых последовательных натуральных чисел делится на 3» надо до­казывать, а чтобы убедиться в истинности предложения «некоторые натуральные числа делятся на 3», достаточно привести конкретный пример?

Чтобы ответить на эти вопросы, необходимо более глубо­кое изучение математических предложений и, прежде всего, высказываний с кванторами.

В формулировках математических предложений часто встре­чаются слова: «каждый», «все», «некоторые», «хотя бы один». Например, свойство противоположных сторон прямоугольника формулируется так: «в любом прямоугольнике противополож­ные стороны равны», а о свойстве натуральных чисел мы гово­рили, что «некоторые натуральные числа кратны 5». Выясним, каков смысл этих слов и как он используются в математике.

Если задана высказывательная форма, то, чтобы превра­тить ее в высказывание, достаточно вместо каждой из пере­менных, входящих в форму, подставить ее значение. Напри­мер, если на множестве N натуральных чисел задана высказы­вательная форма А(х)- «число х кратно 5», то, подставив в нее вместо х число 20, мы получим истинное высказывание «число 20 кратно 5». Если же в эту высказывательную форму подставить вместо д: число 17, мы получим ложное высказы­вание «число 17 кратно 5».

Однако существуют и другие способы получения высказы­ваний из высказывательных форм.

Если перед высказывательной формой «число х кратно 5» поставить слово «всякое», то получится предложение «вся­кое число х кратно 5». Относительно этого предложения можно задать вопрос, истинно оно или ложно. Значит, пред­ложение «всякое число л: кратно 5» (х е N) - высказывание, причем ложное.

Выражение «для всякого х» в логике называется квантором общности по переменной х (переменная может быть обозна­чена и другой буквой) и обозначается символом V х.

Запись (Vx) А(х) означает: «для всякого значения х предло­жение А(х) - истинное высказывание». Иногда эту запись до­полняют обозначением множества X, на котором задана выска- зывательная форма А(х), и тогда предложение (Vx е X) А(х) можно читать:

а) для всякого л; из множества X истинно А(х);

б) всякий элемент из множества X обладает свойством А.

Выражение «существует х такое, что...» в логике называет­ся квантором существования по переменной х (переменная может быть обозначена и другой буквой) и обозначается сим­волом Зх.

Запись (Зх) А(х) означает: «существует такое значение х, что А(х) - истинное высказывание». Иногда эту запись до­полняют обозначением множества X, на котором задана вы- сказывательная форма ^(х), и тогда предложение (ЗхеX) А(х) можно читать:

а) существует такое х из множества X, что истинно А(х)\

б) хотя бы один элемент х из множества X обладает свой­ством^. ^ ^

^ Заметим, что в математике наряду со словом «всякий» i употребляют слова «каждый», «любой», а вместо слова «су- ¹ шествует» используют слова «некоторые», «найдется», «есть», «хотя бы один».

у Обратим внимание на особенность употребления в мате- митике слова «некоторый». В обычной речи, говоря «некото­рые», имеют в виду «по меньшей мере один, но не все», в ма­тематике же слово «некоторые» означает «по меньшей мере один, но, может быть, и все».

Итак, если задана одноместная высказывательная форма то чтобы превратить ее в высказывание, достаточно н1111йть квантором общности или существования содержа­щуюся и ней переменную. Если же высказывательная форма

содержит несколько переменных, то перевести ее в высказы­вание можно, если связать квантором каждую переменную. Например, если дана высказывательная форма «х > у», то для получения высказывания надо связать квантором обе пере­менные: например, (Vx)(3^) х> у или (Зх)(Зу) х> у.

Однако важно уметь не только переходить от высказыва­тельной формы к высказыванию с помощью кванторов, но и распознавать высказывания, содержащие кванторы, и выявлять их логическую структуру. Дело в том, что кванторы содержатся в формулировках определений, теорем и других математиче­ских предложений, хотя часто только подразумеваются. На­пример, в формулировке теоремы «Вертикальные углы равны» квантора в явном виде нет, но предполагается, что данное ут­верждение справедливо для всех вертикальных углов. Записы­вая коммутативное свойство сложения в виде а + b = b + а, под­разумевают, что оно справедливо для любых чисел а и Ь.

Задача 1. Выявить логическую структуру следующих вы­сказываний:

а) Некоторые нечетные числа делятся на 5.

б) Произведение двух любых последовательных натураль­ных чисел кратно 2.

в) В прямоугольнике диагонали равны.

Решение, а) В этом предложении имеется квантор суще­ствования,, он выражен словом «некоторые», и высказыва­тельная форма «нечетные числа делятся на 5», заданная на множестве X нечетных чисел. Обозначим высказывательную форму символом А(х), тогда логическая структура данного предложения такова: (ЗхбЛЭ А(х). Если предложение А(х) записать, используя символы: «х:5», то исходное высказыва­ние можно представить в таком виде: (Зх е X) х:5, где X- множество нечетных чисел.

б) В данном предложении имеется квантор общности, он представлен ' словом «любой», и высказывательная форма «произведение двух последовательных натуральных чисел кратно 2», заданная на множестве N натуральных чисел. Обо­значим ее А(х). Тогда логическая структура данного высказы­вания такова: (Vxe N) А(х). И если А(х) представить в виде х(х + 1):2, то заданное предложение можно записать так: (VxeN) х(х+ 1):2.

в) В заданном высказывании квантора в явном виде нет, но подразумевается, что свойством «иметь равные диагонали» обладают любые прямоугольники, следовательно, этот кван­тор общности можно включить в заданное высказывание, не изменив его сути: «в любом прямоугольнике диагонали рав­ны». Тогда его структура такова: (Ухе X) А(х), где Х- мно­жество прямоугольников, А(х)- высказывательная форма «в прямоугольнике диагонали равны».

Выясним теперь, как устанавливают значения истинности высказываний, содержащих кванторы.

Рассмотрим сначала высказывание с квантором общности, т.е. высказывание вида (Vxe X) А(х). В нем утверждается, что для любого х из множества X истинно А(х), поэтому, чтобы убедиться в истинности этого высказывания, надо показать, что множество истинности Т_А высказывательной формы А(х) совпадает с множеством X (Т_А = X). Чтобы убедиться в лож­ности высказывания (Vxe А) А(х), достаточно показать, что Т_А Ф X, т.е. показать, что существует такое значение х е X, при котором высказывательная форма обращается в ложное высказывание.

Задача 2. Установить, истинны или ложны следующие высказывания:

а) Для каждого х из множества {0, 1, 4} значение выраже­ния (4-х):(2х + 1) есть число целое.

б) Произведение двух любых последовательных натураль­ных чисел кратно 2.

в) Всякое натуральное число делится на 5.

Решение, а) Если мы хотим убедиться в истинности данно­го высказывания, то надо показать, что при подстановке каж­дого числа из множества {0, 1,4} в выражение (4 - х):(2х + 1) получается целое число. Имеем:

если х = 0, то (4-0):(2-0+ 1) = 4:1 =4;

еслих = 1, то (4- 1):(2-1 + 1) = 3:3 = 1;

еслих = 4, то (4-4):(2-4 + 1) = 0:9 = 0.

Действительно, значение выражения (4-х):(2х +1) при всех заданных значениях х есть число целое. Установили мы •)то путем перебора всех возможных случаев.

б) Воспользуемся результатом задачи 1 (случай б) и предста- ним данное высказывание в таком виде: (Vx е N) х(х + 1): 2.

Мы не знаем, истинно оно или ложно, поэтому рассмотрим несколько случаев. Если х = 1, то произведение 1-2 кратно 2, гак как на 2 делится второй множитель. Если х = 2, то произ- нсдсние 2-3 тоже кратно 2, так как на 2 делится первый мно­житель. Если х = 7, то и в этом случае 7-8 кратно 2, поскольку н горой множитель 8 делится на 2. Исходя из рассмотренных илучаев, можно предположить, что данное высказывание ис- тинное, но убедиться в этом путем перебора (как в первом предложении) нельзя, поскольку невозможно перебрать все натуральные значения х. Будем рассуждать. Из двух последо­вательных натуральных чисел одно обязательно четное. Но если в произведении один из множителей делится на 2, то, как известно, и все произведение делится на 2. Следовательно, при любом натуральном х произведение х(х+1) делится на 2.

в) Высказывание «всякое натуральное число делится на 5» - ложное. Убедиться в этом можно, назвав натуральное число, которое не делится на 5, например число 12.

В математике говорят, что в ложности данного высказы­вания мы убедились, приведя контрпример.

Вообще истинность высказывания с квантором общности устанавливается путем доказательства. Показать ложность таких высказываний можно, приведя контрпример.

Заметим, что доказательство истинности высказываний, содержащих квантор общности, можно выполнять различны­ми методами. Решая задачу 2, мы использовали перебор всех возможных случаев и рассуждения. Эти и другие методы до­казательства будут рассматриваться нами позже, в § 4.

Выясним, как устанавливается значение истинности выска­зываний, содержащих квантор существования. В высказыва­нии (Зх е X) А(х) утверждается, что в множестве X есть такой элемент х, которой обладает свойством А. Поэтому оно будет истинно, если множество истинности высказывательной фор­мы А(х) не пусто (Т_А Ф 0). Для того чтобы показать это, дос­таточно найти такое значение переменной х, при котором высказывательная форма А(х) обращается в истинное выска­зывание, т.е. привести пример.

Высказывание (Зх е X) А(х) ложно в том случае, когда Т_А = 0. Убедиться в этом можно лишь путем доказательства.

Задача 3. Установить, истинны или ложны следующие высказывания:

а) Среди треугольников есть прямоугольные.

б) Некоторые прямоугольные треугольники являются рав­носторонними.

Решение, а) Данное высказывание содержит квантор су­ществования, который выражен словом «есть». Чтобы убе­диться в истинности такого высказывания, достаточно при­вести пример. В данном случае прямоугольный треугольник можно начертить.

б) В этом случае квантор существования выражен словом «некоторые». Если считать данное высказывание истинным, то надо привести пример, т.е. попытаться начертить тре­угольник, который был бы одновременно прямоугольным и равносторонним. Из того, что это не удается начертить, еще не следует вывод о ложности данного высказывания. В этом надо убедиться путем доказательства.

Действительно, если треугольник прямоугольный, то в нем один угол равен 90°, а в равностороннем все углы 60°. Следо­вательно, ни один прямоугольный треугольник не может быть равносторонним. Поэтому данное высказывание ложное.

Вообще истинность высказывания с квантором существо­вания устанавливается при помощи конкретного примера. Чтобы убедиться в ложности такого высказывания, необхо­димо провести доказательство.

Заметим, что убедиться в ложности высказывания- это значит опровергнуть его.

Упражнения

1. В высказывании «всякий прямоугольник является четы­рехугольником» выделите квантор и высказывательную фор­му. Переформулируйте данное высказывание, заменив слово «всякий» его синонимом.

2. В высказывании «хотя бы одно из чисел первого десятка составное» выделите квантор и высказывательную форму. Переформулируйте данное высказывание, заменив квантор «хотя бы одно» его синонимом.

3. Прочтите следующие записи, заменив символические обозначения кванторов общности и существования их словес­ными выражениями:

а) (Vx е R) х² - 1 = (х + 1)(х - 1);

б)(3j/eR) 5 + ^ = 5;

в) (Vy € R) у + 3 > 0;

г) (Зх е N) х + 3 < 0.

4. Запишите следующие предложения, используя символи­ческие обозначения кванторов:

а) Существует такое натуральное число х, что х + 5 = 9.

б) Каково бы ни было число х, х + 0 = х.

в) Уравнение ах² + Ьх + с = 0 имеет хотя бы один корень.

5. Запишите, используя символы, следующие высказыва­ния и определите их значения истинности:

а) Всякое число, умноженное на нуль, есть нуль.

Г>) Произведение любого числа и единицы равно этому числу.

н) При делении нуля на любое другое число получается нуль.

I) Квадрат люб