Способ эксцентрических сфер можно применять для построения проекции линии пересечения двух поверхностей, имеющих общую плоскость симметрии. Каждая из этих поверхностей должна содержать семейство окружностей, по которым её могут пересекать эксцентрические сферы, общие для обеих поверхностей.
Пример. Построить линию пересечения тора и кругового конуса, имеющих общую фронтальную плоскость симметрии G (рисунок 4.6.)
Для построения линии пересечения нельзя использовать ни один из раннее рассмотренных способов.
Действительно, при использовании вспомогательных горизонтальных плоскостей уровня на торе получим кривые Персея, на конусе – окружности. Фронтальные плоскости уровня при пересечении с конусом дадут гиперболы, с тором – окружности.
Способ концентрических сфер также нельзя применить, т.к. отсутствует точка пересечения осей i и t заданных тел вращения.
Для решения задачи применим эксцентрические сферы.
Вспомогательные эксцентрические сферы необходимо выбирать так, чтобы они пресекались с тором по его меридиональным круговым сечениям, проецируемым в виде отрезков прямых.
Определяем опорные точки.
Высшая В и низшая А точки определяются на пересечении контурных образующих тора и конуса. Эти точки также являются точками видимости на фронтальной плоскости. Для определения промежуточных точек последовательность построения следующая
1. На фронтальной проекции через центр вращения t (t2) тора намечаем положение ряда меридиональных сечений тора D2,D2¢,D2¢¢,…
2. Из середины полученных круговых сечений тора, проецируемых на фронтальной проекции в виде отрезков прямых (например M2,N2), восстанавливаем перпендикуляры до пересечения с осью i (i2)
 Рисунок 4.6 - Применение способа экцентрических сфер
Рисунок 4.6 - Применение способа экцентрических сфер
|
конуса. Полученные точки О2, О2¢,О2¢ ¢,… определяют центры вспомогательных сфер.
3. Точки C2, D2, E2,…искомой линии пересечения поверхностей тора и конуса устанавливаются на пресечении фронтальных проекции соответствующих окружностей, полученных при взаимном пересечении каждой из заданных поверхностей со вспомогательными сферами. Фронтальные проекции этих окружностей имеют форму отрезков прямых.
Для нахождения горизонтальных проекций точек C, D,E,…необходимо воспользоваться окружностями конической поверхности, которые проецируются на горизонтальную плоскость проекций без искажения.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Гордон В.О., Семенцов – Огиевский М.И. Курс начертательной геометрии. М.: Наука, 2000.272 с.
2.Чекмарев А.А. Начертательная геометрия и черчение. М.: Гуманитарный издательский центр ВЛАДОС, 1999.471 с.
3.Посвянский А.Д. Краткий курс начертательной геометрии.- М.: Высшая школа, 1974.-191 с.
4.Ломоносов Г.Г. Инженерная графика. М.: Недра, 1984.285 с.
5.Нартова Л.Г., Якунин В.И. Начертательная геометрия. Теория и практика. М.: Изд-во Дрофа ISBN, 2008.304с.
6. Фролов С.А. Начертательная геометрия. М.:Изд-во ИНФА – м ISBM-М 2001. 288 c.
Лицензия РБ на издательскую деятельность № 0261 от 10 апреля 1998 г.
Лицензия на полиграфическую деятельность №6848366 от 21 июня 2000 г.
Подписано в печать _______ 2009г. Формат 60х84. Бумага полиграфическая.
Гарнитура Таймс. Усл. печ. л.2,9. Тираж _____экз. Заказ № _______
Издательство Башкирского государственного аграрного университета.
Типография Башкирского государственного аграрного университета.
Адрес издательства и типографии: 450001, г. Уфа, ул. 50 лет Октября, 34
ПРИЛОЖЕНИЕ А

|
ПРИЛОЖЕНИЕ Б
Вариант 1
| Построить линию пересечения шара с цилиндром вращения. Построить развертку указанного в варианте тела с нанесением на ней линии пересечения. | 
|
| № | Шар | R основ. цилиндра | Координаты точки О центра оси | Н высота цилиндра | Основан. параллельное плоскости | Развертка | |||||
| Координаты центра | R шара | ||||||||||
| X | Y | Z | X | Y | Z | ||||||
| XOY | Шара | ||||||||||
| XOY | Цилиндра | ||||||||||
| XOY | Шара | ||||||||||
| XOY | Цилиндра | ||||||||||
| XOY | Шара | ||||||||||
| XOY | Цилиндра | ||||||||||
| XOZ | Шара | ||||||||||
| ZOY | Цилиндра | ||||||||||
| ZOY | Шара | ||||||||||
| XOZ | Цилиндра |
Продолжение ПРИЛОЖЕНИЯ Б
Вариант 3
| Построить линию пересечения цилиндра вращения с конусом вращения (основание конуса параллельно плоскости П1). Построить развертку конуса с нанесением линии пересечения. | 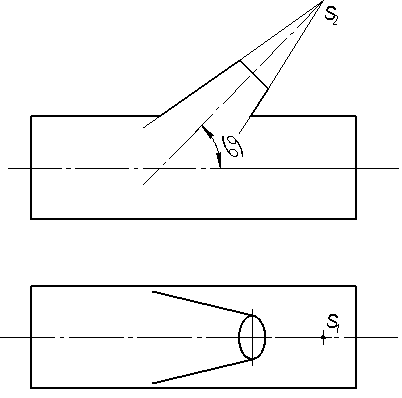
|
| № | Радиус основ. конуса R | Корд. центра основ. конуса | Радиус цилиндра R | Корд. центра основ. цилиндра | Н высота цилиндра | Н высота конуса | a угол наклона оси конуса | ||||
| X | Y | Z | X | Y | Z | ||||||
Продолжение ПРИЛОЖЕНИЯ Б
Вариант 2
| Построить линию пересечения шара радиуса R с прямым круговым цилиндром, радиус основания которого r, а ось цилиндра параллельна фронтальной плоскости проекций и наклонена под углом a к горизонтальной плоскости проекций. Построить развертку цилиндра с нанесением на ней линии пересечения тел. | 
|
| № | R сферы | r цилиндра | Угол a | Координаты центра сферы О¢ | Координаты центра верт. основан. цилиндра О | ||||
| X | Y | Z | X | Y | Z | ||||
| ? | |||||||||
| ? | |||||||||
| ? | |||||||||
| ? | |||||||||
| ? | |||||||||
| ? | |||||||||
| ? | |||||||||
| ? |
Продолжение ПРИЛОЖЕНИЯ Б
Вариант 4
| Построить линию пресечения закрытого тора с поверхностью наклонного цилиндра вращения. Заданные поверхности имеют общую фронтальную плоскость симметрии. Построить развертку цилиндра с нанесением линии пересечения | 
|
| № | Координаты точки А | Координаты точки В | Радиус основания R | Угол наклона a | Радиус основания цилиндра r | ||||
| X | Y | Z | X | Y | Z | ||||
Продолжение ПРИЛОЖЕНИЯ Б
Вариант 5
| Построить линию пересечения цилиндра вращения с конусом вращения. Построить развертку конуса с нанесением линии пересечения поверхностей. Ось цилиндра перпендикулярна профильной плоскости проекций. | 
|
| № | R основ. цилиндра | Координаты основ. цилиндра О¢ | Н высота цилиндра | R основ. конуса | Коорд. центра основ. конуса О | Коорд. вершины конуса S | ||||||
| X | Y | Z | X | Y | Z | X | Y | Z | ||||
ПРИЛОЖЕНИЕ В
Вариант 1, 11, 21

| Вариант 2, 12, 22

|
Вариант 3, 13, 23

| Вариант 4, 14, 24

|
Продолжение ПРИЛОЖЕНИЯ В
Вариант 5, 15, 25

| Вариант 6, 16, 26

|
Вариант 7, 17, 27

| Вариант 8, 18, 28

|
Продолжение ПРИЛОЖЕНИЯ В
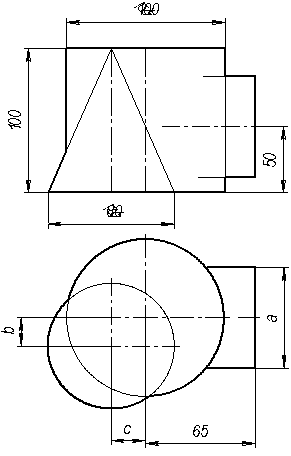
Вариант 9, 19, 29
| Вариант 10, 20, 30

|






