МОДЕЛИРОВАНИЕ СЛУЧАЙНОЙВЕЛИЧИНЫ И
З а д а ч а
1. Провести многократные измерения заданного интервала времени.
2. Построить гистограмму распределения результатов измерения.
3. Вычислить среднее значение и дисперсию полученного распределения.
4. Выполнить сравнение гистограммы с нормальным распределением Гаусса,
имеющим те же среднее и дисперсию, что и экспериментальное распределение.
ВВЕДЕНИЕ
Случайной называется величина, изменяющаяся от опыта к опыту нерегулярно и на первый взгляд беспорядочно. Так, при бросании игральной кости (кубик с нумерованными гранями) может выпасть любое число от 1 до 6. Радиоактивное ядро может распасться в любую наперед избранную секунду, время жизни ядра до распада - случайная величина. При массовом изготовлении любой продукции все изделия оказываются не вполне идентичными по параметрам. Таким образом, те или иные параметры для совокупности таких изделий также являются случайными величинами.
Результат каждого отдельного измерения случайной величины непредсказуем. Но при многократном повторении измерений в неизменных условиях совокупность их результатов описывается статистическими закономерностями. Если бросать игральную кость сотни раз, каждое определенное число (например, два) выпадает примерно в 1/6 части общего числа попыток; для радиоактивного вещества, содержащего очень большое число одинаковых ядер, можно надежно предсказать число распадов за любой (но не слишком малый) наперед заданный промежуток времени. Удается подметить закономерности и в распределении по тому или иному параметру изделий, изготовляемых в массовом производстве по определенной технологии (знание этих закономерностей оказывается полезным как технологу- изготовителю, так и потребителю изделий).
Наряду со случайными встречаются величины неслучайные. Таковы прежде всего фундаментальные физические постоянные: скорость света в вакууме, заряд и масса электрона и т.п. К неслучайным величинам относятся и свойства конкретного образца в конкретных условиях (например, его плотность, теплоемкость и т.п.). Но когда в реальном эксперименте измеряется даже неслучайная величина, из-за совместного действия многочисленных неконтролируемых причин результат отдельного измерения подвергается искажениям и становится величиной случайной. Поэтому изучение статистических закономерностей служит одной из основ теории и практики физического и инженерного эксперимента. Часто принимается, что результаты многократных измерений описываются функцией Гаусса (см. ниже) - так называемым законом нормального распределения.
Закономерности распределения значений изучаемой случайной величины
становятся наглядными, если построить гистограмму – ступенчатую диаграмму, показывающую, как часто при измерениях появляются значения, попадающие в тот или иной из равных интервалов Δt, лежащих между наименьшим tmin и наибольшим tmax из измеренных значений величины t. Гистограмму строят в следующих координатах
(см. рисунок):
ось абсцисс - измеряемая величина t, ось ординат - ΔN/NΔt.
Здесь N - полное количество измерений, ΔN - количество результатов, попавших в интервал [t,t+Δt]. Частное ΔN/N есть доля результатов, попавших в указанный интервал, и характеризуе т вероятность попадания в него результата отдельного измерения. Отношение этой величины к ширине интервала ΔN/NΔt характеризует некоторую "плотность вероятности". При очень большом числе измерений (N→∞) весь диапазон значений t в принципе можно разбить на "бесконечно малые" интервалы dt и подсчитать число результатов dN в каждом из них. Тогда вместо ступенчатой гистограммы получится плавная кривая соответствующая новой функции t:
(1)
Функцию ρ(t) называют плотностью вероятности или законом распределения исследуемой величины.
Нормальное распределение описывается функцией Гаусса
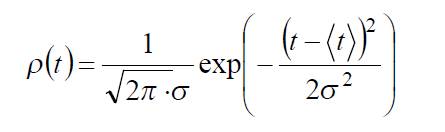
(2)
Чтобы сравнить исследуемое вами распределение с нормальным, проще
всего, найти по данным измерений параметры t и σ (приближенно, так как
число измерений ограничено), вычислить для них функцию ρ(t) по формуле
(2) и построить ее в тех же координатах, что и гистограмму (см. рисунок).
Параметр <t> есть среднее арифметическое всех результатов измерений:
(3)
Параметр σ называется дисперсией. Он характеризует "ширину" нормального
распределения и может быть определен только для бесконечно большого числа измерений. В нашем случае в качестве приближенного значения полагаем:
(4)
Из формулы (2)
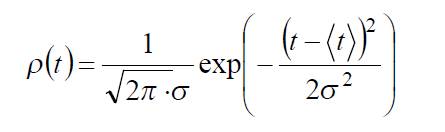
видно, что плотность нормального распределения имеет максимум при t = <t> и симметрична относительно этого значения: следует ожидать, что примерно так же будет выглядеть гистограмма. Можно сравнить "наибольшую высоту гистограммы" и ρmax(t):
(5)
Последнее соотношение получается, если в функции Гаусса положить t= <t>.
Для количественной проверки того, насколько хорошо полученные результаты описываются нормальным распределением, воспользуемся соотношением
(6)
Здесь записано, что вероятность P12 попадания результата каждого измерения в интервал [t1, t2], с одной стороны, может быть вычислена как интеграл функции распределения в этих пределах, а с другой - найдена, как относительное число измерений N12, результаты которых попали в этот интервал.
Разумно использовать значения вероятности для наиболее употребительных в технике измерений пределов. Это вероятности попадания результата измерения в интервалы:
(7)
ИЗМЕРЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ
1. Проведите не менее 50 измерений. Результат каждого измерения (высоту падения линейки) заносите во второй столбец табл. 1.
Т а б л и ц а 1
2. Постройте гистограмму, выполнив для этого следующие операции:
а) отыщите в табл. 1 наименьший hMIN и наибольший hMAX из результатов наблюдений;
б) промежуток (hMIN - hMAX) разбейте на m равных интервалов Δh, соблюдая следующие условия; m должно быть целым, близким к 
(напомним, N – полное число измерений). Измеренные значения hMIN и hMAX должны попадать внутрь "крайних" интервалов; граничные значения, разделяющие соседние интервалы, должны быть по возможности "круглыми" числами - это облегчит построение гистограммы. Границы
выбранных интервалов заносите в первый столбец табл.2.
Т а б л и ц а 2
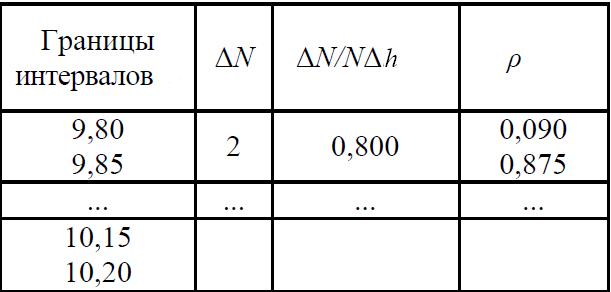
в) подсчитайте число результатов измерений Δ Ni, из табл.1, попавших в каждый из интервалов Δ h, заполнив таким образом второй столбец табл.2;
г) вычислите опытное значение плотности вероятности (третий столбец
табл.2);
д) постройте на миллиметровой бумаге гистограмму.
3. По данным табл.1 вычислите < h > и σ, используя формулы (3) и (4); занесите результаты в "подвал" табл. 1. Вычисление Σ(hi- <h>) ≈ 0 – хороший способ контроля правильности нахождения < h >.
4. По формуле (5) вычислите максимальное значение плотности распределения ρMAX, соответствующее h =< h >, занесите его в "подвал" табл.1. Для значений h, соответствующих границам избранных интервалов, вычислите по формуле (2) значения плотности распределения ρ(h), занесите их в четвертый столбец табл.2. Нанесите все расчетные точки на график, на котором изображена гистограмма, и проводите через них плавную кривую. Удовлетворяет ли вас соответствие кривой и гистограммы? В чем вы видите причины неполного их соответствия?
5. Проверьте, насколько точно выполняется в ваших опытах соотношение (6); вычислите границы интервалов, названных в (7) для найденных
вами < h > и σ, занесите их в табл. 3.
Таблица 3
По данным табл.1 подсчитайте и занесите в табл. 3 число измерений, попадающих в каждый из этих интервалов, и отношение к общему числу измерений N 12 /N. Сравните их с соответствующими нормальному распределению значениями вероятности Р 12. Считаете ли вы такое совпадение удовлетворительным? В чем видите расхождение? Результат любого измерения должен быть приведен с указанием погрешности, которая в случае многократных прямых измерений определяется как сумма приборной и случайной погрешностей. При определении случайной погрешности используют не дисперсию, определенную выше, а среднеквадратичное отклонение от среднего значения в серии результатов:
(8)
Распределение, относящееся к конечному числу измерений, называется распределением Стьюдента. Оно при N → ∞ переходит в нормальное (гауссовское) распределение. Случайная погрешность результата многократных измерений равна: Δ h = tN σ < h > (9).
где tαN - коэффициент Стьюдента, зависящий от числа измерений N и доверительной вероятности α: α = P (h Î [< h >-Δ h, < h >+Δ h ]).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Являются ли, по вашему мнению, случайными следующие физические величины: а) плотность алмаза при 20°С, б) напряжение сети; в) сопротивление резистора, взятого наугад из партии с одним и тем же номинальным сопротивлением; г) число молекул в 1 см3 при нормальных условиях? Приведите другие примеры случайных и неслучайных физических величин.
2. Изучая распределение ЭДС партии электрических батареек, студент использовал цифровой вольтметр. После нескольких измерений получились такие результаты (в вольтах): 1,50; 1,49; 1,50; 1,50; 1,49. Имеет ли смысл продолжать измерения? Что бы вы изменили в методике этого эксперимента?
3. При обработке результатов измерений емкости партии конденсаторов получено: <С> = 1,1 мкФ, σ = 0,1 мкФ. Если взять коробку со 100 конденсаторами из этой партии, то сколько среди них можно ожидать конденсаторов с емкостью меньше 1 мкФ? больше 1,3 мкФ?
