Программа и методические указания к лабораторным работам для студентов заочного отделения специальности 140611 “Электроизоляционная, кабельная и конденсаторная техника”
г. Пермь
2006г.
УДК 621.316
Программа и методические указания к лабораторным работам по курсу
«Надежность электрической изоляции»
Составитель: Гиберт Д.П.
Приводится программа самостоятельного изучения дисциплины «Надежность электрической изоляции», а также методические указания и варианты заданий к лабораторным работам.
Предназначен для студентов заочной формы обучения.
Утверждено на заседании кафедры
от ”“2006г. Протокол №
Программа дисциплины, методические указания и варианты заданий к лабораторным работам предназначены для студентов-заочников специальности 140611, самостоятельно изучающих дисциплину «Надежность электрической изоляции». При изучении дисциплины необходимо ознакомиться с учебным планом (табл. 1), учебной программой (табл. 2), изучить темы дисциплины и выполнить две лабораторные работы.
Учебный план
Таблица 1
| Группа | Курс | Семестр | Количество часов | Вид контроля | |||
| Всего | Лекций | Лабор. Занятий | Самост. Работа | ||||
| КТЭИз | Зачет |
Программа дисциплины
Таблица 2
| Раздел | Количество часов | ||
| Лекции | Лабор. Занятий | Самост. Работа | |
| Часть 1. Общая теория надежности | |||
| 1.1. Возникновение и сущность проблемы надежности | |||
| 1.2. Основные понятия и характеристики надежности | |||
| 1.3. Надежность нерезервированных систем без восстановления | |||
| 1.4. Надежность невосстанавливаемых систем с резервированием | |||
| 1.5. Надежность систем в период эксплуатации | |||
| Часть 2. Надежность электрической изоляции | |||
| 2.1. Характеристики надежности электрической изоляции | |||
| 2.2. Вывод уравнения "кривой жизни" электрической изоляции | |||
| 2.3. Частичные разряды в твердой изоляции | |||
| 2.4. Функция распределения местной напряженности поля | |||
| 2.5. Уравнение надежности электрической твердой изоляции | |||
| 2.6. Расчет времени до отказа твердой изоляции | |||
| 2.7. Функция безотказной работы жидкой и газообразной изоляции | |||
| Часть 3. Условия работы электрической изоляции | |||
| 3.1. Классификация действующих на изоляцию нагрузок | |||
| 3.2. Электрические напряжения | |||
| 3.3. Температурные условия работы | |||
| 3.4. Механические напряжения | |||
| 3.5. Прочие воздействия. Выбор расчетных условий эксплуатации |
Основной формой изучения дисциплины является самостоятельная работа студента над рекомендованной литературой и электронным вариантом конспекта лекций.
Целью дисциплины «Надежность электрической изоляции» является изучение методов измерения надежности и методы повышения сроков службы изделий кабельной и электроизоляционной техники.
Изучение курса ставит задачу приобретения студентами знания общей теории надежности, навыков расчета времени до отказа электрической изоляции и знания основных характеристик надежности электрической изоляции.
По курсу выполняется две лабораторные работы. Лабораторные работы представляют собой занятия в компьютерном классе по созданию программных продуктов автоматического расчета основных характеристик надежности. 1-ая лабораторная работа проводится по общей теории надежности, 2-ая лабораторная работа проводится по надежности электрической изоляции. Выполняется отчет по лабораторной работе, который должен содержать:
1) Титульный лист
2) Задание на лабораторную работу
3) Краткая теория по теме лабораторной работы
4) Результат решения (графики, значения)
5) Листинг разработанной программы
6) Выводы по лабораторной работе
Лабораторные работы защищаются преподавателю по соответствующим темам.
Лабораторные работы выполняются на кафедре КТЭИ, в ауд. 202 к. А.
Методические указания и задания по выполнению лабораторных работ:
Лабораторная работа №1 "Расчет основных характеристик надежности"
Задание (необходимо выполнить одно из указанных преподавателем):
1) На испытания было поставлено определенное число объектов, через определенные промежутки времени подсчитывали количество отказавших объектов. Разработать программу по автоматическому расчету вероятности отказа Q(ti), вероятности безотказной работы P(ti), плотности распределения отказов f(ti), интенсивности отказов λ(ti), среднего времени наработки на отказ T и дисперсии Dt. Найти значения характеристик для своего варианта (таблица 3). Результаты оформить в виде таблицы. Построить графики зависимости Q(t), P(t), f(t), λ(t) от времени испытания.
Таблица 3
| ti, час | |||||||||||
| № вар. | Число отказавших элементов | сумма | |||||||||
| 1.1 | |||||||||||
| 1.2 | |||||||||||
| 1.3 | |||||||||||
| 1.4 | |||||||||||
| 1.5 | |||||||||||
| 1.6 | |||||||||||
| 1.7 | |||||||||||
| 1.8 | |||||||||||
| 1.9 | |||||||||||
| 1.10 | |||||||||||
| 1.11 | |||||||||||
| 1.12 | |||||||||||
| 1.13 | |||||||||||
| 1.14 | |||||||||||
| 1.15 | |||||||||||
| 1.16 | |||||||||||
| 1.17 | |||||||||||
| 1.18 | |||||||||||
| 1.19 | |||||||||||
| 1.20 | |||||||||||
| 1.21 | |||||||||||
| 1.22 | |||||||||||
| 1.23 | |||||||||||
| 1.24 | |||||||||||
| 1.25 | |||||||||||
| ti, час | |||||||||||
| № вар. | Число отказавших элементов | сумма | |||||||||
| 2.1 | |||||||||||
| 2.2 | |||||||||||
| 2.3 | |||||||||||
| 2.4 | |||||||||||
| 2.5 | |||||||||||
| 2.6 | |||||||||||
| 2.7 | |||||||||||
| 2.8 | |||||||||||
| 2.9 | |||||||||||
| 2.10 | |||||||||||
| 2.11 | |||||||||||
| 2.12 | |||||||||||
| 2.13 | |||||||||||
| 2.14 | |||||||||||
| 2.15 | |||||||||||
| 2.16 | |||||||||||
| 2.17 | |||||||||||
| 2.18 | |||||||||||
| 2.19 | |||||||||||
| 2.20 | |||||||||||
| 2.21 | |||||||||||
| 2.22 | |||||||||||
| 2.23 | |||||||||||
| 2.24 | |||||||||||
| 2.25 |
Указания по выполнению:
Статистически определить вероятность отказа 
по результатам испытаний можно с помощью следующей формулы:
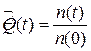
где n(t) – число отказавших объектов к моменту времени t.
Вероятность безотказной работы P(t):
Статистическая оценка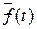 
производится за интервал времени Δ t, так как функция f(t) является дифференциальной:
Интенсивность отказов λ(t):
Среднее время наработки на отказ T определяется как математическое ожидание времени до отказа:
Дисперсия наработки до отказа Dt:
Где Ti – время до отказа i -ой группы объектов, ni+1 – количество отказавших за следующий промежуток объектов.
2) Известна формула вероятности безотказной работы некоторого объекта по показательному закону распределения. Необходимо разработать программу по автоматическому построению графиков зависимости P (τ), Q (τ), f (τ), λ(τ) от времени (τ=0..100 часов), построить графики для своего варианта и найти значения P (τ), Q (τ), f (τ), λ(τ) для τ=5, 10, 20, 100 часов.
Варианты задания: для 1-ой группы: 
, для 2-ой группы: 
, где V – номер варианта.
Указания по выполнению:
Вероятность отказа Q(t):
Плотность распределения отказов f(t):
Интенсивность отказов λ(t):
3) Известна формула плотности вероятности отказов некоторого объекта по показательному закону распределения. Необходимо разработать программу по автоматическому построению графиков зависимости P (τ), Q (τ), f (τ), λ(τ) от времени (τ=0..100 часов), построить графики для своего варианта и найти значения P (τ), Q (τ), f (τ), λ(τ) для τ=5, 10, 20, 100 часов.
Варианты задания: для 1-ой группы: 
, для 2-ой группы: 
, где V – номер варианта.
Указания по выполнению:
Если известна плотность вероятности отказов, то можно определить вероятность отказов или вероятность безотказной работы:
4) Известны параметры закона распределения Вейбулла для некоторого объекта. Необходимо разработать программу по автоматическому построению графиков зависимости P (τ), Q (τ), f (τ), λ(τ) от времени (τ=0..100 часов), построить графики для своего варианта и найти значения P (τ), Q (τ), f (τ), λ(τ) для τ=5, 10, 20, 100 часов.
Варианты задания: λ0=0,02 для всех вариантов; для 1-ой группы: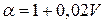 
, для 2-ой группы: 
, где V – номер варианта.
Указания по выполнению:
В программу вводятся формулы основных характеристик надежности по закону распределения Вейбулла:
5) Известны параметры закона гамма-распределения для некоторого изделия с n резервными элементами. Необходимо разработать программу по автоматическому построению графиков зависимости P (τ), Q (τ), f (τ), λ(τ) от времени (τ=0..100 часов), построить графики для своего варианта и найти значения P (τ), Q (τ), f (τ), λ(τ) для τ=5, 10, 20, 100 часов.
Варианты задания: для 1-ой группы: 
, для 2-ой группы: 
, где V – номер варианта.
| № вар. | 5, 10, 15, 20, 25 | 1, 6, 11, 16, 21 | 2, 7, 12, 17, 22 | 3, 8, 13, 18, 23 | 4, 9, 14, 19, 24 |
| n |
Указания по выполнению:
В программу вводятся формулы основных характеристик надежности по закону гамма-распределения:
Γ(α) – гамма-функция, для которой параметр α равен суммарному количеству объектов, поэтому α= n.
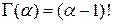
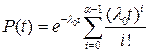
6) Пусть имеется система с n элементами, которые составляют облегченный резерв. Все элементы n -кратно резервированной группы с облегченным резервированием подчинены экспоненциальному закону надежности. Необходимо разработать программу по автоматическому построению графиков зависимости P (τ), Q (τ), f (τ), λ(τ) от времени (τ=0..100 часов), построить графики для своего варианта и найти значения P (τ), Q (τ), f (τ), λ(τ) для τ=5, 10, 20, 100 часов.
Варианты задания: для 1-ой группы: 
, 
; для 2-ой группы: 
, 
, где V – номер варианта. Число n взять из 5-го задания.
Указания по выполнению:
В программу автоматического расчета характеристик надежности вводятся формулы для систем с облегченным резервированием:
