Лабораторная работа № 4
Получение передаточных функций по задающему и возмущающему воздействиям, построение структурно- алгоритмической схемы и исследование характеристик двигателя постоянного тока независимого возбуждения
| Исходные данные:
Тип двигателя
Номинальная мощность P н, кВт
Скорость вращения n н, об/мин
Ток нагрузки I н, А
Сопротивление обмотки якоря и добавочных полюсов 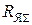 = r я + r дп, Ом
Число параллельных ветвей якоря 2 а
Число витков полюса параллельной обмотки 
Магнитный поток полюса Ф, мВб
Номинальный ток возбуждения параллельной обмотки I в, А
Момент инерции якоря J, кг×м2.
|
| Рисунок 1 - Схема включения двигателя постоянного тока независимого возбуждения |
Составление дифференциальных уравнений и передаточных функций ДПТ НВ
Система дифференциальных уравнений, описывающая процессы, протекающие в двигателе, имеет вид:
(1)
где 
- напряжение обмотки возбуждения двигателя, В;
- ток обмотки возбуждения, А;
- сопротивление обмотки возбуждения, Ом;
- индуктивность катушки возбуждения, Гн;
- напряжение двигателя, В;
- ток, протекающий через якорь двигателя, А;
- индуктивность обмотки якоря, Гн;
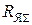- сопротивление обмотки якоря и добавочных полюсов, Ом;
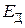- ЭДС двигателя, 
;
- конструктивный коэффициент;
- угловая скорость двигателя, об/мин;
Ф – магнитный поток, Вб;
М – момент двигателя, 
;
- момент сопротивления, ;
- ток сопротивления, А;
J – момент инерции якоря, 
,
Для создания математической модели ДПТ НВ приняты следующие допущения:
1. Система абсолютно жесткая, то есть двигатель имеет одну степень свободы;
2. Масса вращающихся частей постоянна;
3. Статический момент, приведенный к валу двигателя, постоянный;
4. Реакция якоря скомпенсирована;
5. Зависимость угловой скорости вращения вала двигателя от напряжения якоря U я линейная;
6. Поток двигателя неизменен, Ф =const;
7. Температура обмоток не изменяется.
С учетом принятых допущений и подстановки 
уравнение электрического равновесия цепи якоря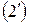 
примет вид:
. (2)
Подстановка 
в уравнение для моментов 
дает
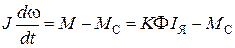. (3)
Выразив из (3) ток якоря двигателя
(4)
и взяв его производную
, (5)
подставляем в (2).
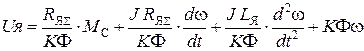
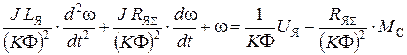(6)
Принимаем следующие обозначения:
электромеханическая постоянная времени
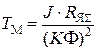; (7)
электромагнитная постоянная времени якорной цепи
; (8)
передаточный коэффициент двигателя по напряжению якоря
; (9)
передаточный коэффициент двигателя по статическому моменту (возмущающему воздействию)
. (10)
Подставив принятые обозначения (7) – (10) в уравнение статического равновесия (6), получаем дифференциальное уравнение двигателя, записанное относительно регулируемой величины , при входном U я и возмущающем М с воздействиях:
(11)
В операторной форме (
) при нулевых начальных условиях уравнение (11) примет вид:
(12)
В результате математического преобразования дифференциального уравнения (12) определяем передаточную функцию ДПТ НВ по задающему и возмущающему воздействиям:
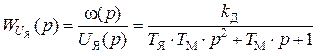(13)
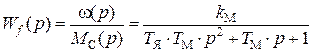(14)
