Позиционные системы счисления

Раздел 3. Технические средства информационных технологий

Лекция № 6. Информационные основы построения ЭВМ

 

1. Общие сведения о системах счисления. Позиционные системы счисления.

2. Методы перевода чисел.

3. Представление информации в цифровых автоматах.

 

Литература: 1. Острейковский В.А. Информатика: Учеб. для вузов. –

М.: Высш. шк., 1999.

2. Основы вычислительной техники и программирование:

Учебник / Под ред. Ю.А.Бузунова.- М.: Воениздат, 1981.

 

 

Общие сведения о системах счисления.

Позиционные системы счисления

 

Общие сведения о системах счисления

 

Системой счисления называют совокупность приемов построе­ния, обозначения и наименования чисел. Каждая система счис­ления включает:

1) определенный набор символов (цифр) для изображения чисел; эти символы называются базисными числами и составляют конечный алфавит

{ x₁, x₂, …, x_n },

 

2) определенный способ чтения (наименования) чисел.

 

Например:

в десятичной системе счисления алфавит состоит из десяти цифр:

0, 1, 2, 3, 4, …, 9;

в двоичной – из двух цифр: 0, 1;

в римской системе счисления – из семи цифр:

1, 5, 10, 50, 100, 500, 1000, которые обозначаются, соответственно, знаками: I, V, X, L, C, D, M;

 

Каждой цифре в записи числа однозначно сопоставляется ко­личество, выражаемое этой цифрой. Это количество будем назы­вать количественным эквивалентом цифры. Если x_i –цифра, за­писанная в конкретном месте в записи числа, то (x_i) – ее количест­венный эквивалент.

По способу определения количественного эквивалента цифры в записи числа все системы счисления можно разбить на два класса: непозиционные и позиционные.

 

Система счисления называется непозиционной, если значение числового знака (каждой цифры) не зависит от его расположения в записи числа.

 

Классическим примером непозиционной системы счисления является римская система счисления. Исторически вначале появились непозиционные системы счис­ления. Общим недостатком этих систем счисления является трудность записи в них больших чисел: либо эти записи слишком громоздки, либо алфавит цифр весьма велик. Именно поэтому непозиционные системы счисления в вычислительной технике не нашли применения.

 

 

Позиционные системы счисления

 

Система счисления называется позиционной, если количественный эквивалент каждой цифры определяется не только видом символа, ее изображающего, но и ее положением в записи числа. При этом место цифры в записи числа называется разрядом.

 

Классическим примером позиционной системы счисления является десятичная система счисления.

В таблице 1 приведены примеры некоторых, наиболее часто употребляемых, позиционных систем счисления.

Таблица 1

Основание	Система счисления	Знаки
	Двоичная Восьмеричная Десятичная Шестнадцатеричная	0, 1 0, 1, 2, 3, 4, 5, 6, 7 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F

 

Одним из основных понятий в позиционных системах счисле­ния является вес разряда. Весом j - го разряда для позиционной системы счисления называется отношение количественного эквивалента цифры x_i, стоящей в j -м разряде, к количественному эквиваленту той же цифры, стоящей в нулевом разряде:

 

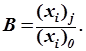
Число, указывающее сколько единиц младшего разряда содержится в единице старшего разряда,называется основанием позиционной системы счисления.

 

Существует связь между основанием системы счисления и числом цифр, используемых в системе счисления (это видно из таблицы 1): для представ­ления любого числа конечным числом разрядов в системе счис­ления с основанием K достаточно иметь K цифр. Обычно эти K цифр составляют отрезок натурального ряда целых положитель­ных чисел, включая 0. Таким образом, алфавит K - ичной системы счис­ления имеет вид {0, 1, 2,..., K-1 }.

Любое число Х в К - ичной позиционной системе счисления можно представить в виде полинома от основания К:

 

Х_(К) = x_n-1K^n-1 + x_n-2K^n-2 + … + x₁K + x₀K⁰ + x_-1K^-1 + x_-2K^-2 + … + x_-mK^-m =

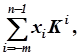= (1)

 

где x_i – значение цифры в i – ом разряде;

K_i – основание системы счисления;

n, m – число разрядов в целой и дробной части числа, соответственно;

i – порядковый номер разряда.

 

Основание системы счисления обычно указывают (при необходимости) в виде десятичного индекса справа в нижней части числа.

 

Приме­ры:

23,43 ₍₁₀₎ = 2×10¹ + 3×10⁰ + 4×10^-1 + 3×10^-2

 

(в данном примере знак «3» в одном случае означает число единиц, а в другом - число сотых долей единицы);

 

451,2 ₍₈₎ = 4×8² + 5×8¹ + 1×8⁰ + 2×8^-1.

 

Краткая запись числа представляется последовательностью цифр, каждой из которых можно поставить в соот­ветствие определенную позицию. Обычно позиции, предназначенные для представления целой части числа, отделяют от позиций, предназначенных для представления дробной части числа – запятой:

 

Х_(К) = x_n-1 x_n-2 … x₁ x₀, x_-1 x_-2 … x_-m.

 

Запятая сама позиции не занимает, а является началом отсчета номера позиции: все позиции влево от запятой, предна­значенные для хранения целой части числа, нумеруются в поряд­ке возрастания натурального ряда чисел 0, 1, 2,..., п- 1, а все позиции вправо от запятой, предназначенные для хранения дробной части числа, нумеруются целыми отрицательными числами - 1, - 2,...., - т. Таким образом, позиция цифры с присвоенным ей номером называется разрядом числа.

На рисунке 1 показана нумерация разрядов в разрядной сетке ЭВМ, включающей п разрядов для представления целой и т раз­рядов – для представления дробной части числа. Под разрядной сеткой ЭВМ понимают общеечисло разрядов, отводимое для представления как целой, так и дробной части числа в цифровой вычислительной ма­шине.

 

n - 1

n - 2

…

-1

-2

…

-m

 

Рисунок 1 - Нумерация разрядов в разрядной сетке ЭВМ