Методы аналоговой модуляции

Чтобы передать сигнал по каналам связи, нужно воспользо­ваться каким-либо переносчиком. В качестве переносчика естествен­но использовать те материальные объекты, которые имеют свойство перемещаться в пространстве, например, переменный ток в проводах (проводная связь), электромагнитное поле в открытом пространстве (радиосвязь), световой луч (оптическая связь). На рисунке 4 показано использование шкалы частот и волн различных типов для различных видов связи.

 

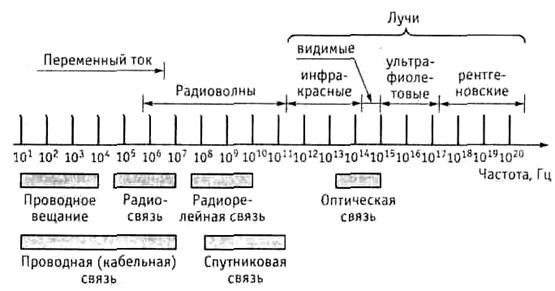
Рисунок 4 – Использование шкалы частот в электросвязи

 

В пункте передачи первичный сигнал необходимо преобразовать в сигнал, удобный для его передачи по соответствующей среде распространения. В пункте приема выпол­няется обратное преобразование. Доставленный в пункт приема сигнал должен быть снова преобра­зован в сообщение и затем передан получателю.

Обычно в качестве переносчика сигнала используют гармоническое коле­бание – которое называют несущим колебанием. Процесс преобразова­ния первичного сигнала заключается в изменении одного или не­скольких параметров несущего колебания по закону изменения пер­вичного сигнала (т.е. в наделении несущего колебания признаками первичного сигнала) и называется модуляцией. Аналоговая модуляция является таким способом физического кодирования, при котором информация кодируется изменением амплитуды, частоты или фазы несущего колебания. Основные способы аналоговой модуляции показаны на рисунке 5. На диаграмме (рисунок 5, а) показана последовательность бит исходной информации, представленная потенциалами высокого уровня для логической единицы и потенциалом нулевого уровня для логического нуля. Такой способ кодирования называется потенциальным кодом,

который часто используется при передаче данных между блоками компьютера.

 

Рисунок 5 – Различные типы модуляции

 

При амплитудной модуляции (рисунок 5, б) для логической единицы выбирается один уровень амплитуды синусоиды несущего колебания, а для логического нуля – другой. Этот способ редко используется в чистом виде на практике из-за низкой помехоустойчивости (воздействие помех в канале связи приводит к искажению амплитуды передаваемого сигнала и, соответственно, к искажению передаваемой информации), но часто применяется в сочетании с другим видом модуля­ции – фазовой модуляцией (квадратурная амплитудная модуляция в модемах с повышенной скоростью передачи данных).

При частотной модуляции (рисунок 5, в) значения 0 и 1 исходных данных пере­даются синусоидами с различной частотой – f₁ и f₂. Этот способ модуляции не требует сложных схем в модемах и обычно применяется в низкоскоростных моде­мах, работающих на скоростях 300 или 1 200 бит/с.

При фазовой модуляции (рисунок 5, г) значениям данных 0 и 1 соответствуют сигналы одинаковой частоты и амплитуды, но с различной фазой, например 0 и 180 градусов или 0, 90, 180 и 270 градусов.

 

 

Цифровое кодирование

 

Как известно, в вычислительной технике для представления данных используется двоичный код (цифровой код). Как было показано ранее, любой аналоговый сигнал (а таковых большинство в природе) может быть преобразован в цифровой сигнал. Такое преобразование выполняется в два этапа: на первом этапе осуществляется дискретизация аналогового сигнала по времени (то есть получают дискретные выборки аналогового сигнала), а на втором этапе – квантование дискретных выборок по уровню (при этом амплитуде каждой выборки ставится в соответствие п -разрядный двоичный код).

Внутри компьютера единицам и нулям данных соответствуют дискретные электрические сигналы. Представление данных в виде электрических или оптичес­ких сигналов называется кодированием. Существуют различные способы кодирова­ния двоичных цифр 1 и 0, например, потенциальный способ (рисунок 1, а), при котором единице соответствует один уровень напряжения, а нулю – другой, или импульсный спо­соб (рисунок 1, б), когда для представления цифр используются импульсы различной или одной полярности.

Цифровое кодирование может быть использовано и при передаче данных на незначительные расстояния (десятки – сотни метров) по кабельным или волоконно-оптическим линиям связи.

При использовании прямоугольных импульсов для передачи дискретной инфор­мации необходимо выбрать такой способ кодирования, который одновременно до­стигал бы нескольких целей:

- имел при одной и той же битовой скорости наименьшую ширину спектра ре­зультирующего сигнала;

- обеспечивал синхронизацию между передатчиком и приемником;

- обладал способностью распознавать ошибки;

- обладал низкой стоимостью реализации.

Более узкий спектр сигналов позволяет на одной и той же линии (с одной и той же полосой пропускания) добиваться более высокой скорости передачи данных. Кроме того, часто к спектру сигнала предъявляется требование отсутствия постоянной составляющей, то есть наличия постоянного тока между передатчиком и приемником. В частности, применение различных трансформаторных схем гальванической развязки препятствует прохождению постоянного тока.

Синхронизация передатчика и приемника нужна для того, чтобы приемник точно знал, в какой момент времени необходимо считывать новую информацию с линии связи. Эта проблема в сетях решается сложнее, чем при обмене данными между близко расположенными устройствами, например между блоками внутри компьютера или же между компьютером и принтером. На небольших расстояниях хорошо работает схема, основанная на отдельной тактирующей линии связи (рисунок 6), так что информация снимается с линии данных только в момент прихода тактового импульса. В сетях использование этой схемы вызывает трудности из-за неоднородности характеристик проводников в кабелях. На больших расстояниях неравномерность скорости распространения сигнала может привести к тому, что тактовый импульс придет несколько позже или раньше соответствующего сигнала данных, и бит данных будет пропущен или считан повторно. Другой причиной, по которой в сетях отказываются от использования тактирующих импульсов, является экономия проводников в дорогостоящих кабелях.

 

Рисунок 6 – Синхронизация приемника и передатчика

на малых расстояниях

 

С учетом названных причин в сетях применяются так называемые самосинхронизирующиеся коды, сигналы которых несут для передатчика указания о том, в какой момент времени нужно осуществлять распознавание очередного бита (или нескольких бит, если код ориентирован более чем на два состояния сигнала). Любой резкий перепад сигнала – так называемый фронт – может служить хорошим указанием для синхронизации приемника с передатчиком.

При использовании синусоид в качестве несущего сигнала результирующий код обладает свойством самосинхронизации, так как изменение амплитуды несущей частоты дает возможность приемнику определить момент появления входного кода.

Требования, предъявляемые к методам кодирования, являются взаимно противоречивыми, поэтому каждый из рассматриваемых ниже методов цифрового кодирования обладает своими преимуществами и своими недостатками по сравнению с другими.

На рисунке 7 приведены некоторые наиболее популярные цифровые коды.

На рисунке 7, а показан уже упомянутый ранее метод потенциального кодирования, называемый также кодированием без возвращения к нулю (Non Return to Zero, NRZ). Последнее название отражает то обстоятельство, что при передаче последователь­ности единиц сигнал не возвращается к нулю в течение такта. Метод NRZ прост в реализации, обладает хорошей распознаваемостью ошибок, но не обладает свойством самосинхро­низации. Даже при наличии высокоточного тактового генератора приемник может ошибиться с моментом съема данных, так как частоты двух генераторов никогда не бывают полностью идентичными. Другим серьезным недостатком метода NRZ является наличие низкочастотной составляющей, которая приближается к нулю при передаче длинных последова­тельностей единиц или нулей. Из-за этого многие каналы связи, не обеспечивающие прямого гальванического соединения между приемником и источником, этот вид кодирования не поддерживают. В результате в чистом виде код NRZ в сетях не используется.

 

Рисунок 7 – Способы дискретного кодирования данных

 

Одной из модификаций метода NRZ является метод биполярного кодирования с альтернативной инверсией (Bipolar Alternate Mark Inversion, AMI). В этом методе (рисунок 7, б) используются три уровня потенциала – отрицательный, нулевой и положительный. Для кодирования логического нуля используется нулевой потен­циал, а логическая единица кодируется либо положительным потенциалом, либо отрицательным, при этом потенциал каждой новой единицы противоположен по­тенциалу предыдущей.

Код AMI частично ликвидирует проблемы постоянной составляющей и отсут­ствия самосинхронизации, присущие коду NRZ. В целом, для различных комбинаций бит на линии использование кода AMI приводит к более узкому спектру сигнала, чем для кода NRZ, а значит, и к более высокой пропускной способности линии.

В коде AMI используются не два, а три уровня сигнала на линии. Дополнитель­ный уровень требует увеличение мощности передатчика примерно в полтора раза для обеспечения той же достоверности приема бит на линии, что является общим недо­статком кодов с несколькими состояниями сигнала по сравнению с кодами, кото­рые различают только два состояния.

Существует код, похожий на AMI, но только с двумя уровнями сигнала. При пере­даче нуля он передает потенциал, который был установлен в предыдущем такте (то есть не меняет его), а при передаче единицы потенциал инвертируется на противо­положный. Этот код называется потенциальным кодом с инверсией при единице (Non Return to Zero with ones Inverted, NRZI). Код удобен в тех случаях, когда использование третьего уровня сигнала весьма нежелательно, например, в оптичес­ких кабелях, где устойчиво распознаются два состояния сигнала – свет и темнота.

Кроме потенциальных кодов в сетях используются и импульсные коды, когда дан­ные представлены полным импульсом или же его частью – фронтом. Наиболее простым случаем такого подхода является биполярный импульсный код, в котором единица представлена импульсом одной полярности, а ноль – другой (рисунок 7, в). Каждый импульс длится половину такта. Такой код обладает отличными самосин­хронизирующими свойствами, но постоянная составляющая может присутство­вать, например, при передаче длинной последовательности единиц или нулей. Кроме того, спектр у него шире, чем у потенциальных кодов, поэтому биполярный импульсный код используется редко.

В локальных сетях до недавнего времени самым распространенным методом коди­рования был так называемый манчестерский код (рисунок 7, г). Он применяется в технологиях Ethernet и Token Ring.

В манчестерском коде для кодирования единиц и нулей используется перепад потенциала, то есть фронт импульса. При манчестерском кодировании каждый такт делится на две части. Информация кодируется перепадами потенциала, про­исходящими в середине каждого такта. Единица кодируется перепадом от низкого уровня сигнала к высокому, а ноль – обратным перепадом. В начале каждого такта может происходить служебный перепад сигнала, если нужно представить несколь­ко единиц или нулей подряд. Так как сигнал изменяется, по крайней мере, один раз за такт передачи одного бита данных, то манчестерский код обладает хорошими самосинхронизирующими свойствами. Полоса пропускания манчестерского кода в среднем в полтора раза уже, чем у биполярного импульсного кода. У него также нет постоянной составляющей.

Манчестерский код имеет еще одно преимущество перед биполярным импульсным кодом. В нем используется для передачи данных два уровня сигнала, а не три.

 

 

Спектры сигналов

 

Все сигналы могут быть подразделены на периодические и непе­риодические. Периодическим называется сигнал, значения которого повторяют­ся через определенные равные промежутки времени, называемые периодом повторения сигнала (Т), или просто периодом. Для непериоди­ческого сигнала это условие не выполняется.

Простейшим периодическим сигналом является гармоническое ко­лебание (рисунок 8, а):

 

s(t) = S sin(wt),

 

где S, w - соответственно амплитуда и угловая частота колебания, равная

 

w = 2pf = 2p / Т.

 

Рисунок 8 – Простейшие периодические сигналы

Другим примером периодического сигнала является последова­тельность прямоугольных импульсов (рисунок 8, б). Можно показать, что такая последовательность импульсов является результатом сложения большого числа гармонических колебаний (в общем случае – бесконечного) с разными амплитудами, частотами и начальными фазами.

На рисунке 9 показан процесс синтеза последовательности прямоугольных импульсов с использованием гармонических колебаний. В качестве исходной синусоиды вы­берем такую, у которой период колебаний совпадает с периодом Т прямоугольных импульсов (рисунок 9, а, б):

 

s(t) = S₁ sin(w₁t),

 

Колебание заданной частоты w₁ и амплитуды S₁ можно представить в виде графика: на оси частот отметить значение w₁ и изобразить вертикальную линию высотой, равной амплитуде сигнала S₁ (рисунок 9, б).

Следующая синусоида имеет частоту колебаний в 3 раза боль­шую, а амплитуду – в 3 раза меньшую. Сумма этих двух синусоид пока еще ма­ло похожа на прямоугольные импульсы (рисунок 9, в). Но если до­бавить к ним синусоиды с частотами колебаний в 5, 7, 9, 11 и т.д. раз большими, а с амплитудами в 5, 7, 9, 11 и т.д. раз меньшими, то сум­ма всех этих колебаний будет не так уж сильно отличаться от последовательности прямоугольных импульсов.

 

 

Рисунок 9 – Периодическая последовательность прямоугольных

импульсов (а) и формирование ее сигнала (б – д)

 

Может показаться, что представление прямоугольных импульсов в виде совокупности синусоид есть не более чем математический при­ем и не имеет никакого отношения к реальности. Однако это не так. Радиоинженерам хорошо знакомы приборы (они называются анали­заторами спектров), которые позволяют выделить каждую входящую в сложный сигнал синусоиду.

Тот факт, что сигнал произвольной формы (а не только прямоугольные импульсы) можно разложить на сумму обыкновенных синусоид, доказал в 20-х годах XIX века французский математик Ж. Фурье.Такой набор синусоид получил название спектра сигнала.

Каждый сигнал имеет свой сугубо индивидуальный спектр. Гармонические колебания, составляющие спектр сигнала, называются гармоническими составляющими сигнала или просто гармониками.

Линии (рисунок 9) на графике, соответствующие амплитудам гармоник, называются спектральными линиями. Распределение амплитуд гармоник по частоте называется спектром амплитуд сигнала.

Так как спектр периодического сигнала состоит из отдельных спек­тральных линий, его называют дискретным (или линейчатым).

Частота первой гармоники сигнала определяется, как показано выше, периодом сигнала: w₁ = 2p / Т. Если период сигнала оставить неизменным, а изменять только длительность импульсов t (рисунок 10, а и в), то частота первой гармоники будет той же самой для обоих сигна­лов. Изменится скорость убывания амплитуд гармоник (рисунок 10, б и г). Чем короче импульс, тем медленнее убывают амплитуды гармоник и тем соответственно, большим числом гармоник следует представ­лять прямоугольные импульсы, чтобы сохранить достаточную степень их «прямоугольности».

 

Рисунок 10 – Изменение спектра амплитуд при уменьшении

длительности импульсов

 

Существует очень важное понятие – практическая ширина спек­тра сигнала. Интуитивно ясно, что если полоса пропускания какого-либо устройства недостаточно широкая, чтобы пропустить все гармо­ники, существенно влияющие на форму сигнала, то сигнал на выходе этого устройства будет искаженным. Таким образом, можно сказать, что шири­на полосы пропускания устройства не должна быть уже ширины спек­тра сигнала.

Что же следует считать шириной спектра сигнала, если число гар­моник в сигнале бесконечно? Существует несколько критериев для определения практической ширины спектра сигнала. Например, мож­но отбрасывать все гармоники с амплитудами меньшими 1 % макси­мальной амплитуды в спектре, тогда частоты оставшихся гармоник и определят ширину спектра сигнала. Можно отбрасывать те гармони­ки, суммарная энергия которых меньше 10 % общей энергии сигнала. В этом случае ширину спектра также определяют оставшиеся в сиг­нале гармоники.

Однако независимо от критерия, по которому определяют ширину спектра сигнала, можно выделить такие общие для всех сигналов за­кономерности: чем круче фронт сигнала, чем короче импульсы и чем больше пауза между импульсами, тем шире во всех этих случаях спектр сигнала, т.е. тем медленнее убывают амплитуды гармоник с ростом их номера.

На практике при использовании в качестве сигналов прямоугольных импульсов в качестве ширины спектра сигнала чаще всего принимается диапазон частот от w = 0 до w = 2p / t.

Все, что сказано выше, относится к периодическим сигналам (в частности, к бесконечной последовательности прямоугольных импульсов).

Непериодический сигнал легко получить из периодического, увели­чивая период вплоть до Т® ¥. При увеличении периода сигнала частота первой гармоники w₁ = 2p / Т понижается. Спектральные линии становятся гуще. Ампли­туды гармоник уменьшаются. Последнее становится понятным, если учесть, что энергия сигнала, оставаясь неизменной, перераспреде­ляется теперь между возросшим числом гармоник. Естественно, доля каждой гармоники в сигнале падает.

Следовательно, при переходе к непериодическому сигналу (нап­ример, к одиночному импульсу) мы получаем в спектре такого сигнала вместо отдельных гармоник бесконечно большое число синусоидаль­ных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда каждого такого колебания становит­ся исчезающе малой, потому что на его долю приходится бесконечно малая часть энергии сигнала. Другими словами, в любой бесконечно узкой полосе частот мы всегда обнаружим синусоидальное колеба­ние, правда, бесконечно малой амплитуды.

Понятие спектра амплитуд в последнем случае лишено смысла и заменяется понятием спектральной плотно­сти амплиту (рисунок 11), которая указывает, по сути, на удельный вес беско­нечно малой амплитуды синусоидального колебания в любой беско­нечно узкой полосе частот.

Таким образом, спектр непериодического сигнала является в общем случае не дискретным, а непрерывным.

 

Рисунок 11 – Спектральная плотность амплитуд одиночного

прямоугольного импульса длительностью t

Ранее отмечалось, что при передаче данных в сетях кроме импульсных сигналов используются модулированные колебания.

Спектр результирующего модулированного сигнала зависит от типа модуляции и скорости модуляции, то есть желаемой скорости передачи бит исходной информации.

Рассмотрим сначала спектр сигнала при потенциальном кодировании. Пусть логическая единица кодируется положительным потенциалом, а логический ноль – отрицательным потенциалом такой же величины. Для упрощения вычислений пред­положим, что передается информация, состоящая из бесконечной последователь­ности чередующихся единиц и нулей. В этом случае в течение одного периода передается два бита данных.

Если дискретные данные передаются с битовой скоростью N бит/с, то спектр состоит из постоянной составляющей нуле­вой частоты и бесконечного ряда гармоник с частотами f₀, 3f₀, 5f₀, 7f₀,..., где f₀ = N/2. Амплитуды этих гармоник убывают достаточно медленно – с коэффициентами 1/3, 1/5, 1/7,... от амплитуды гармоники f₀ (рисунок 12, а). В результате спектр потенци­ального кода требует для качественной передачи широкую полосу пропускания. Кроме того, нужно учесть, что реально спектр сигнала постоянно меняется в зави­симости от того, какие данные передаются по линии связи. Например, передача длинной последовательности нулей или единиц сдвигает спектр в сторону низких частот, а в крайнем случае, когда передаваемые данные состоят только из единиц (или только из нулей), спектр состоит из гармоники нулевой частоты.

 

Рисунок 12 – Спектры модулированных сигналов

 

 

При переда­че чередующихся единиц и нулей постоянная составляющая отсутствует. Поэтому спектр результирующего сигнала потенциального кода при передаче произволь­ных данных занимает полосу от некоторой величины, близкой к 0 Гц, до примерно 7 f₀ (гармониками с частотами выше 7 f₀ можно пренебречь из-за их малого вклада в результирующий сигнал). Для канала тональной частоты (проводной линии связи) верхняя граница при потенциальном кодировании достигается для скорости передачи данных в 971 бит/с (действительно, f_max = 7f₀ = 971* 7 / 2 = 3 395 Гц при наибольшей частоте АЧХ канала 3 400 Гц), а нижняя неприемлема для любых скоростей, так как полоса пропускания канала начинается с 300 Гц. В результате потенциальные коды в проводных линиях связи никогда не используются.

При амплитудной модуляции спектр состоит из синусоиды несущей частоты f_с и двух боковых гармоник: (f_с + f_м) и (f_с – f_м), где f_м – частота изменения информа­ционного параметра синусоиды, которая совпадает со скоростью передачи данных при использовании двух уровней амплитуды (рисунок 12, б). Частота f_м определяет пропускную способность линии при данном способе кодирования. При небольшой частоте модуляции ширина спектра сигнала будет также небольшой (равной 2 f_м), поэтому сигналы не будут искажаться линией, если ее полоса пропускания будет больше или равна 2 f_м. Для проводной линии связи такой способ модуляции приемлем при скорости передачи данных не больше 3 100 / 2= 1 550 бит/с. Если же для представления данных используются 4 уровня амплитуды, то пропускная спо­собность канала повышается до 3 100 бит/с.

При фазовой и частотной модуляции спектр сигнала получается более слож­ным, чем при амплитудной модуляции, так как боковых гармоник здесь образует­ся более двух, но они также симметрично расположены относительно основной несущей частоты, а их амплитуды быстро убывают. Поэтому эти виды модуляции также хорошо подходят для передачи данных по проводным линиям связи.

Для повышения скорости передачи данных используют комбинированные методы моду­ляции. Наиболее распространенными являются методы квадратурной амплитудной модуляции. Эти методы основаны на сочетании фазовой модуляции с 8 значениями величин сдвига фазы и амплитудной модуляции с 4 уровнями амплитуды. Однако из возможных 32 комбинаций сигнала используются далеко не все. Например, в решетчатых кодах допустимы всего 6, 7 или 8 комбинаций для представления исходных данных, а остальные комбинации являются запрещенными. Такая избыточность кодирования требуется для распознавания модемом ошибочных сигналов, являющихся след­ствием искажений из-за помех, которые на телефонных каналах, особенно коммутируемых, весьма значительны по амплитуде и продолжительны по времени.