Алгоритм граф путь работоспособность

Введение

 

Определение достижимости населенного пункта в системе односторонних дорог рассматривается при помощи некоторого математического объекта, называемого графом.

Граф — это совокупность непустого множества вершин и наборов пар вершин (связей между вершинами).

Наиболее эффективным алгоритмом нахождения кратчайшего пути является алгоритм Дейкстры.

Основная задача данного курсового проекта: определение достижимости населенного пункта в системе односторонних дорог. Решить задачу можно средством программирования. В данной курсовой работе задача была решена в среде C++ Builder.

 

Техническое задание

 

Программа определения достижимости населенного пункта в системе односторонних дорог. Описание: даны несколько населенных пунктов, соединенных между собой (произвольным образом) односторонними дорогами некоторой длины. Определить, есть ли населенный пункт, из которого можно добраться до каждого из остальных пунктов, проезжая не более 100 км. Отобразить решение графически, выделив цветом найденный результат.

1.1 Основания для разработки

 

Основанием для разработки программы является задание к курсовому проекту по предмету «Программирование».

 

Функциональное и эксплуатационное назначение изделия

 

Перечень требований пользователя к программному изделию.

Программа должна обеспечивать:

- удобный интерфейс;

- лёгкость в использовании;

- оптимальность при использовании физических ресурсов компьютера.

 

1.3 Методологические ограничения

Часто попадаются задачи, в условиях которых заданы некоторые объекты и между некоторыми их парами имеются определенные связи. Если объекты изобразить точками (вершинами), а связи - линиями (ребрами), соединяющими соответствующие пары точек, то получится рисунок, называемый графом. Историю теории графов принято исчислять с 1736 г., когда Эйлер исследовал "задачу о кенигсбергских мостах": построить в графе циклический путь, проходящий по одному разу через каждое ребро. В середине 19-го века Гамильтон заинтересовался задачей построения циклического пути, проходящего по одному разу через каждую вершину графа. В это же время графы использовали для анализа электрических цепей (Кирхгоф) и химических молекул (Кэли). Развитие современной теории графов относится к 30-м годам 20-го столетия. Они нашли многочисленные применения в электротехнике, электронике, биологии, экономике, программировании и в других областях.

 

1.3.1 Общие сведения о графах

алгоритм граф путь работоспособность

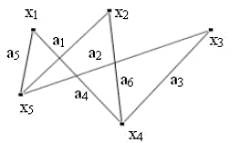
Граф G (рис.1.1) задается множеством точек (вершин) х₁, х₂,..., х_n. (которое обозначается через Х) и множеством линий (ребер) а₁, а₂,...,а_m. (которое обозначается символом А), соединяющих между собой все или часть этих точек. Таким образом, граф G полностью задается (и обозначается) парой (Х, А). Если ребра из множества А ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным графом.

 

 

	Рис. 1.1 Граф G Граф G		Рис. 1.2Пути и последовательности дуг

 

Например, если дорога имеет не двух-, а одностороннее движение то направление этого движения будет показано стрелкой.

Если ребра не имеют ориентации, то граф называется неориентированным, (двухстороннее движение).

В ориентированном графе дуга обозначается упорядоченной парой, состоящей из начальной и конечной вершин, ее направление предполагается заданным от первой вершины ко второй. Путем (или ориентированным маршрутом) ориентированного графа называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.

Так, на рис. 1.2 путями являются последовательности дуг:

а₆, а₅, а₉, а₈, а₄. (1)

а₁, а₆, а₅, а₉. (2)

а₁, а₆, а₅, а₉, а₁₀, а₆, а₄. (3)

 

Ориентированной цепью (орцепью) называется такой путь, в котором каждая дуга используется не больше одного раза.

Простой орцепью называется такой путь, в котором каждая вершина используется не более одного раза. Например, путь (2).

Маршрут есть неориентированный “двойник” пути, и это понятие рассматривается в тех случаях, когда можно пренебречь направленностью дуг в графе. Таким образом, маршрут есть последовательность ребер a₁, a₂,..., a_q, в которой каждое ребро а_i, за исключением первого и последнего ребер, связано с ребрами а_i-1 и а_i+1 своими концевыми вершинами.

В графе, изображенном на рис. 1.2, являются маршрутами; две точки над символом дуги означают, что ее ориентацией пренебрегают, т.е. дуга рассматривается как неориентированное ребро. Также путь или маршрут можно изображать последовательностью вершин. Например, путь (1) будет выглядеть следующем образом: х₂, х₅, х₄, х₃, х₅, х₆. Иногда дугам графа приписываются числа, называемые весом, стоимостью, или длиной этой дуги. В этом случае граф называется графом с взвешенными дугами. А если вес приписывается вершинам графа, то тогда получается граф с взвешенными вершинами. Если в графе веса приписаны и дугам и вершинам, то он называется просто взвешенным.

При рассмотрении пути µ представленного последовательностью дуг (a₁, a₂,..., a_q), за его вес принимается число l(µ), равное сумме весов всех дуг, входящих в µ, т.е

 

1.3.2 Алгоритм Дейкстры

На этом шаге приводится описание алгоритма Дейкстры.

Напомним, что алгоритм Дейкстры разработан для нахождения кратчайшего пути между заданным исходным узлом и любым другим узлом сети.

В процессе выполнения этого алгоритма при переходе от узла i к следующему узлу j используется специальная процедура пометки ребер. Обозначается через u_i кратчайшее расстояние от исходного узла 1 до узла i, через d_ij - длину ребра (i, j). Тогда для узла j определим метку [u_j,следующим образом:

[u_j, i] = [u_i + d_ij, i], d_ij >= 0

Метки узлов в алгоритме Дейкстры могут быть двух типов: временные и постоянные. Временная метка впоследствии может быть заменена на другую временную, если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус временной метки изменяется на постоянный.

Вычислительная схема алгоритма состоит из следующих шагов.

Шаг 0. Исходному узлу (узел 1) присваивается метка [0, -]. Полагаем i = 1.

Шаг i. а) Вычисляются временные метки [u_i + d_ij, i] для всех узлов j, которые можно достичь непосредственно из узла i и которые не имеют постоянных меток. Если узел j уже имеет метку [u_j, k], полученную от другого узла k, и если u_i + d_ij < u_j, тогда метка [u_j, k] заменяется на [u_i + d_ij, i].

b) Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка [u_r, s] с наименьшим значением расстояния u_r среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i = r и повторяем шаг i.

Пример. На рисунке 2 показана транспортная сеть, состоящая из пяти городов (расстояния между городами (в километрах) приведены возле соответствующих дуг сети). Необходимо найти кратчайшие расстояния от города 1 (узел 1) до всех остальных четырех городов.

Рис.2. Транспортная сеть

Шаг 0. Назначаем узлу 1 постоянную метку [0, -].

Шаг 1. Из узла 1 можно достичь узлов 2 и 3. Вычисляем метки для этих узлов, в результате получаем следующую таблицу меток:

Узел Метка Статус метки

1 [0, -] Постоянная

2 [0 + 100, 1] = [100, 1] Временная

3 [0 + 30, 1] = [30, 1] <-Временная

Среди узлов 2 и 3 узел 3 имеет наименьшее значение расстояния (u₃ = 30). Поэтому статус метки этого узла изменяется на "постоянная".

Шаг 2. Из узла 3 (последнего узла с постоянной меткой) можно попасть в узлы 4 и 5. Получаем следующий список узлов:

Узел Метка Статус метки

1 [0, -] Постоянная

2 [100, 1] Временная

3 [30, 1] Постоянная

4 [30 + 10, 3] = [40, 3] <-Временная

5 [30 + 60, 3] = [90, 3] Временная

Временный статус метки [40, 3] узла 4 заменяется на постоянный (u₄ = 40).

 

Шаг 3. Из узла 4 можно достичь узлов 2 и 5. После вычисления меток получим следующий их список:

Узел Метка Статус метки 1[0, -] Постоянная 2[40 + 15, 4] = [55, 4] <-Временная 3[30, 1] Постоянная 4[40, 3] Постоянная 5[90, 3] или [40 + 50, 4] = [90, 4] Временная

 

Временная метка [100, 1], полученная узлом 2 на втором шаге, изменена на [55, 4]. Это указывает на то, что найден более короткий путь к этому узлу (проходящий через узел 4). На третьем шаге узел 5 получает две метки с одинаковым значением расстояния u₅ = 90.

Шаг 4. Из узла 2 можно перейти только в узел 3, но он уже имеет постоянную метку, которую нельзя изменить. Поэтому на данном шаге получаем такой же список меток, как и на предыдущем шаге, но с единственным изменением: метка узла 2 получает статус постоянной. С временной меткой остается только узел 5, но так как из этого узла нельзя попасть ни в какой другой, процесс вычислений заканчивается.

Алгоритм позволяет проводить вычисления непосредственно по схеме сети, как показано на рисунке 3.

Рис.3 Вычисления по схеме (в скобках указан номер шага)

Кратчайший маршрут между узлом 1 и любым другим узлом определяется начиная с узла назначения путем прохождения их в обратном направлении с помощью информации, представленной в постоянных метках. Например, для определения кратчайшего маршрута между узлами 1 и 2 получаем такую обратную последовательность узлов: (2) -> [55, 4] -> (4) -> [40, 3] -> (3) -> [30, 1] -> (1).

Таким образом, получаем путь 1->3->4->2 общей длиной 55 километров.

 

Программная совместимость

 

Программа должна работать под управлением операционной систем Windows 98/NT/XP/Vista/se7en/Win8.