Дифференциальные уравнения

1. Задачи, приводящие к понятию дифференциальных уравнений. Дифференциальные уравнения 1 порядка: определение, общее и частное решение. Начальные условия. Геометрическая трактовка. Порядок, степень дифференциальных уравнений.

2. Понятие о задаче Коши. Теорема существований и единственности.

3. Уравнения с разделенными и разделяющимися переменными.

4. Уравнения однородные относительно Х и У.

5. Линейные дифференциальные уравнения 1 порядка: однородные и неоднородные (метод замены переменной и вариации произвольной постоянной).

6. Уравнение Бернулли.

7. Дифференциальные уравнения высших порядков. Общие понятия. Уравнения, допускающие понижение порядка: , , .

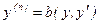8. Однородные линейные уравнения 2 порядка. Структура общего решения. Линейно-независимые решения. Определитель Вронского. Теорема об определителе Вронского.

9. Линейные неоднородные дифференциальные уравнения 2 порядка. Структура общего решения.

10. Линейные неоднородные дифференциальные уравнения 2 порядка: , где 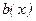- произвольная функция. Метод вариации произвольной постоянной.

11. Линейные дифференциальные уравнения 2 порядка с постоянными коэффициентами, однородные. Характеристическое уравнение. Определение общего решения, если:

- корни характеристического уравнения действительные различные,

- корни характеристического уравнения действительные корни характеристического уравнения действительные равные,

- корни характеристического уравнения действительные комплексно-сопряженные.

12. Неоднородные линейные дифференциальные уравнения 2 порядка с постоянными коэффициентами: . Нахождение частного и общего решения.

13. Неоднородные линейные дифференциальные уравнения 2 порядка с постоянными коэффициентами: . Нахождение частного решения.

14. Линейные уравнения высших порядков. Метод вариации.

15. Система дифференциальных уравнений с постоянными коэффициентами. Определение, решение нормальной системы.

 

Ряды

1. Понятие числового ряда, сумма ряда. Сходящиеся и расходящиеся ряды.

2. Геометрическая прогрессия. Выяснить поведение ряда при различных значениях знаменателя прогрессии.

3. Теорема о свойствах числового ряда (отбрасывание членов ряда, суммирование рядов, умножение на постоянный множитель).

4. Необходимое условие сходимости ряда. гармонический ряд.

5. Теоремы сравнения.

6. Признак Даламбера.

7. Интегральный признак Коши.

8. Знакочередующиеся ряды. Теорема Лейбница.

9. Ряды с произвольными членами. Условная и абсолютная сходимость. Теорема (достаточный признак сходимости знакопеременного ряда).

10. Функциональные ряды. Точки сходимости ряда. Область сходимости.

11. Теорема об интегрировании и дифференцировании равномерно-сходящихся рядов.

12. Степенные ряды. Теорема Абеля.

13. Радиус и интервал сходимости степенного ряда. Теорема об определении радиуса сходимости степенного ряда.

14. Свойства степенных рядов (без доказательства).

15. Ряд Тейлора и Маклорена. Необходимое и достаточное условия для разложения функции в ряд Тейлора.

16. Разложение в ряд Маклорена функции вида: , , .

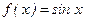17. Биномиальный ряд.

18. Разложение в ряд функции: , , .

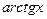19. Приближенное вычисление значений функции. Оценка ошибки.

20. Вычисление определенных интегралов с помощью рядов.

 

Тригонометрические ряды

1. Достаточное условие разложимости функции в ряд Фурье. Кусочно - монотонные функции.

2. Ряд Фурье для четных и нечетных функций.

3. Ряд Фурье для функции с периодом 2е.

4. Разложение в ряд Фурье функций, заданных на полупериоде.

ОБРАЗЦЫ РЕШЕНИЯ ЗАДАНИЙ

КОНТРОЛЬНАЯ РАБОТА № 7

Контрольная работа № 7 состоит из пяти задач. Ниже рассмотрены варианты решения заданий.

 

Образец выполнения заданий № 271 – 280.

Найти общее решение уравнения и частное решение, удовлетворяющее начальному условию

Решение. Преобразуем уравнение: , . Это линейное уравнение 1 порядка. Сделаем замену .

Тогда , .

Составим систему

Решаем первое уравнение: , , , , (при решении этого уравнения постоянную интегрирования можно не писать), . Подставим во второе уравнение, и решим его.

, , , , .

Следовательно 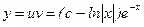- общее решение дифференциального уравнения. Для нахождения частного решения применим условия , т.е. подставим , в общее решение: , отсюда .

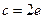Значит 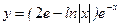- частное решение дифференциального уравнения.

 

 

Образцы выполнения заданий № 281 – 290.

1. Найти общее решение уравнения 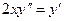и частное решение, удовлетворяющее начальным условиям , .

Решение. Уравнение 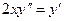не содержит 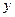, поэтому делаем замену (). Тогда , , , , , , , , , 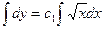- общее решение дифференциального уравнения.

Чтобы найти частное решение, используем начальные условия. Имеем

отсюда

Значит, искомое частное решение таково: .

2. Найти общее решение уравнения и частное решение, удовлетворяющее начальным условиям .

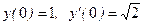Решение. Уравнение не содержит , поэтому делаем замену . Тогда , , , , , , 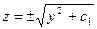или , , 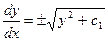, , , 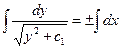= общее решение дифференциального уравнения.

Переходим к нахождению частного решения. Имеем

Подставив сюда начальные условия, получим

Второе равенство удовлетворяется, если взять знак «+». Тогда , .

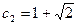Отсюда 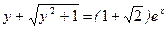- частное решение дифференциального уравнения.

 

Образец выполнения заданий № 291 – 300.

Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям , .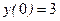

Решение. Сначала найдем общее решение , где - решение соответствующего однородного уравнения, - частного решение.

Составляем характеристическое уравнение и находим его корни , где - минимальная единица.

Отсюда .

Частное решение ищем в таком виде, который соответствует правой части исходного уравнения, а именно .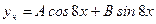

Чтобы найти А, В, подставим это выражение в исходное уравнение

.

Вычислив производные и упростив левую часть, получим

, отсюда будем иметь систему

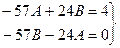, решение которой , .

Следовательно ,

.

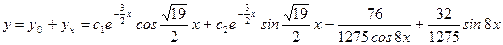Производная этой функции равна

.

Подставим начальные условия: при , , 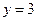. Получим

, ,

отсюда

, .

Ответ: частное решение таково

.

 

Образец выполнения заданий № 301 – 310.

Уменьшение интенсивности света, прошедшего через слой какой-либо среды, пропорционально толщине слоя и интенсивности падающего на него света. Известно, что при прохождении через слой толщины 1 см интенсивность уменьшается в 2 раза. Во сколько раз уменьшится интенсивность при прохождении через слой толщины 5 см?

Решение. Пусть - интенсивность света, падающего внутри среды на поверхность, координата которой х (рис. 1). Согласно условию, при прохождении через последующий бесконечно тонкий слой dx начальная интенсивность уменьшится на величину

,

 

 

 

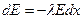Рисунок 1

 

где - коэффициент пропорциональности. Найдем общее решение этого уравнения

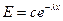, , , (А)

Возьмем произвольный слой , толщина которого 1 см. Пусть при , тогда по условию при будет . Подставив эти значения в (А), получим , отсюда находим , 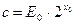. Подставив эти значения в (А), получим . Возьмем - поверхность, удаленная от начальной 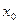на 5 см. Тогда интенсивность будет равна . Отношение исходной интенсивности 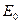к конечной равно

, т.е. интенсивность уменьшилась в 32 раза.

 

Образец выполнения заданий № 311 – 320.

Найти общее решение системы .

Решение. Из первого уравнения находим (А), подставим во второе уравнение , , - получилось линейное однородное уравнение с постоянными коэффициентами. Его характеристическое уравнение имеет корни , , поэтому . Подставив в (А), получим . Следовательно, общее решение системы имеет вид , .

КОНТРОЛЬНАЯ РАБОТА № 8

Контрольная работа № 8 состоит из пяти задач. Ниже рассмотрены варианты решения заданий.

 

Образец выполнения заданий № 321 – 330.

Исследовать на сходимость числовой ряд .

Решение. Проверяем сходимость ряда по признаку Даламбера. Имеем

, отсюда ,

 

Получилось , следовательно наш ряд сходится.

 

Образец выполнения заданий № 331 – 340.

Найти интервал сходимости степенного ряда .

Решение. Имеем

, отсюда ,

.

Потребуем, чтобы было ; тогда , , . Таким образом, внутри интервала исходный ряд сходится абсолютно. Исследуем сходимость на концах этого интервала.

При исходный ряд становится числовым:

; сравним этот ряд с рядом , который расходится:

- получилось число больше 0, поэтому ряд подобен ряду , т.е. расходится.

При исходный ряд становится таким:

- знакочередующийся ряд, который нужно исследовать по признаку Лейбница. Сравним с :

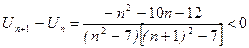при больших 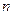; таким образом , т.е. члены ряда уменьшаются по абсолютной величине. Кроме того

, т.е. члены ряда стремятся к 0. Следовательно, знакочередующийся ряд сходится. Таким образом - интервал сходимости исходного степенного ряда.

 

Образец выполнения заданий № 341 – 350.

Вычислить интеграл с точностью до путем предварительного разложения подынтегральной функции в ряд.

Решение. Применим формулу разложения в ряд

Тогда

.

 

Образец выполнения заданий № 351 – 360.

Найти три первых отличных от нуля члена разложения в степенной ряд функции , являющейся частным решением дифференциального уравнения , .

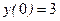Решение. Искомое решение имеет вид

 

(А)

Имеем

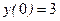
, отсюда

, отсюда

Подставив эти значения в (А), получим ответ

 

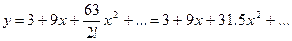
Образец выполнения заданий № 361 – 370.

Функцию в интервале (0, 3) разложить в ряд: а) косинусов, б) синусов.

Решение.

а) Разложение в ряд косинусов имеет вид , где , .

В нашем случае интервал (0, 3) имеет длину , поэтому

,

. Поэтому .

Это выражение можно упростить, если заметить, что

Тогда .

б) Разложение в ряд синусов имеет вид , где

.

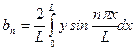В нашем случае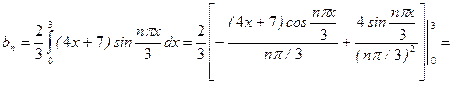

.

Поэтому . Ввиду того, что , это равенство можно записать так .

 

ВАРИАНТЫ КОНТРОЛЬНЫХ ЗАДАНИЙ

КОНТРОЛЬНАЯ РАБОТА № 7

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

В задачах 271 – 280 найти общее решение дифференциального уравнения первого порядка.

271. . 272. .

273. . 274. .

275. . 276. .

277. . 278. .

279. . 280. .

В задачах 281 – 290 найти общее решение дифференциального уравнения второго порядка.

281. . 282. .

283. . 284. .

285. . 286. .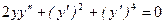

287. 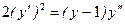. 288. .

289. 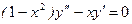. 290. .