Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Высказывания и формулы.
2. Представить в ССФ предикат 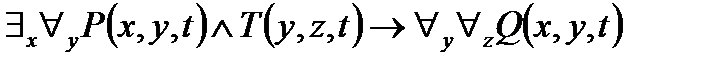 .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 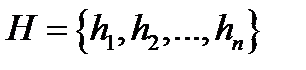 и утверждения и утверждения 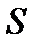 , доказать справедливость выражения , доказать справедливость выражения 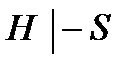 . .
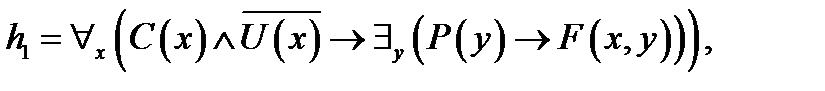 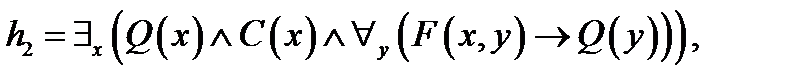
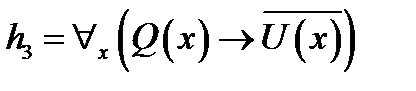 , , 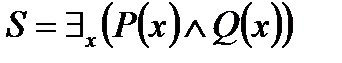 .
4. Найти функцию .
4. Найти функцию 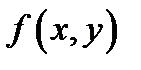 , полученную из функций , полученную из функций 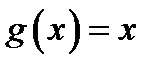 и и 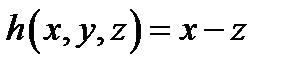 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 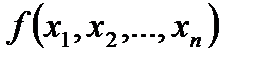 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 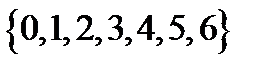 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Выполнимые и общезначимые формулы. Определить вид формулы.
2. Представить в ССФ предикат 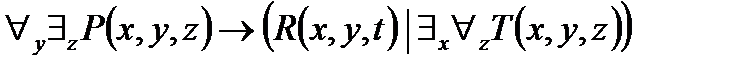 .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 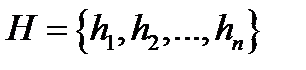 и утверждения и утверждения 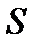 , доказать справедливость выражения , доказать справедливость выражения 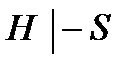 . .
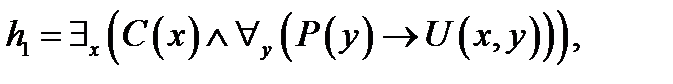 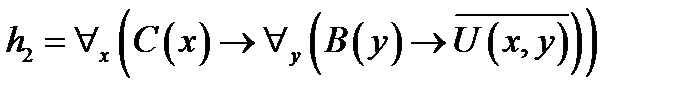 , ,
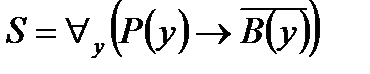 .
4. Найти функцию .
4. Найти функцию 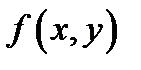 , полученную из функций , полученную из функций 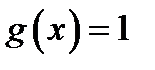 и и 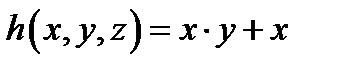 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 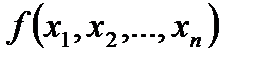 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 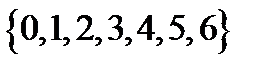 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Алгебраический подход. Основные тождества.
2. Представить в ССФ предикат 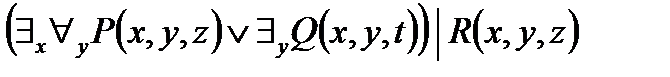 .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 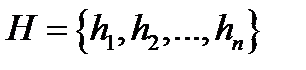 и утверждения и утверждения 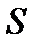 , доказать справедливость выражения , доказать справедливость выражения 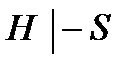 . .
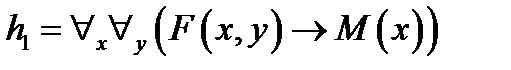 , , 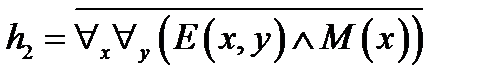 , , 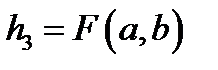
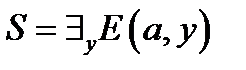 .
4. Найти функцию .
4. Найти функцию 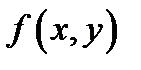 , полученную из функций , полученную из функций 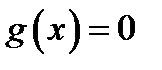 и и 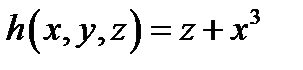 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 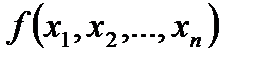 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 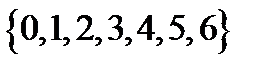 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Дизъюнкты и нормальные формы. Алгоритм нормализации.
2. Представить в ССФ предикат 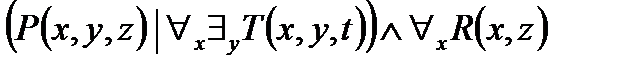 .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 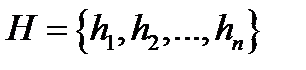 и утверждения и утверждения 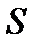 , доказать справедливость выражения , доказать справедливость выражения 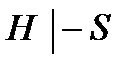 . .
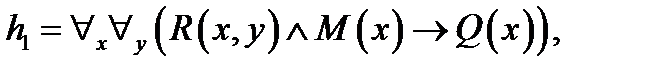 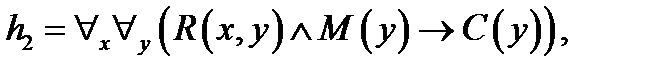 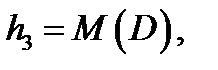 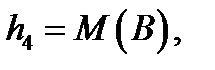 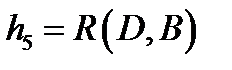 , , 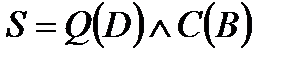 .
4. Найти функцию .
4. Найти функцию 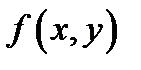 , полученную из функций , полученную из функций 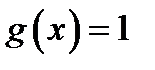 и и 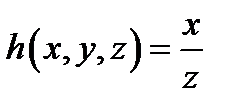 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 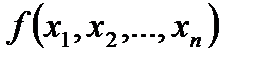 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 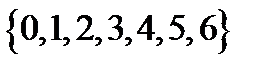 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Дизъюнкты и нормальные формы. Алгоритм нормализации.
2. Представить в ССФ предикат  .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 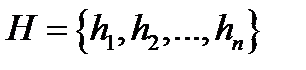 и утверждения и утверждения 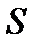 , доказать справедливость выражения , доказать справедливость выражения 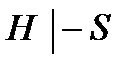 . .
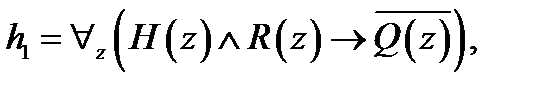 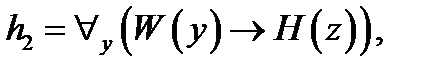 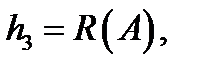  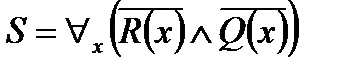 .
4. Найти функцию .
4. Найти функцию 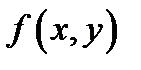 , полученную из функций , полученную из функций 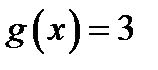 и и 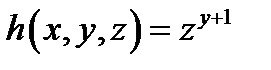 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 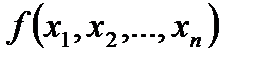 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 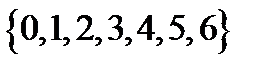 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Типы совместимых высказываний.
2. Представить в ССФ предикат 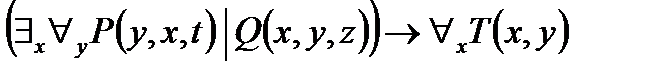 .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 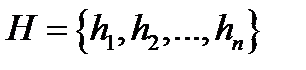 и утверждения и утверждения 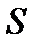 , доказать справедливость выражения , доказать справедливость выражения 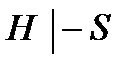 . .
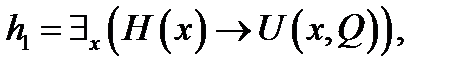 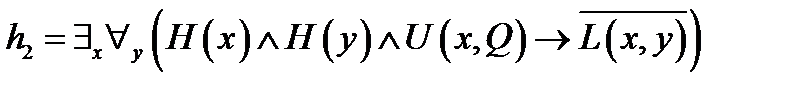
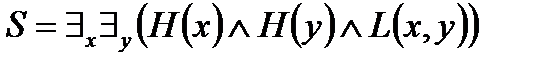 .
4. Найти функцию .
4. Найти функцию 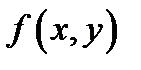 , полученную из функций , полученную из функций 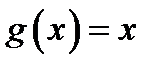 и и 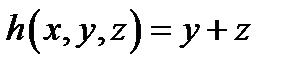 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 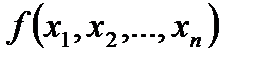 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 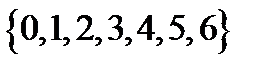 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 7
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Типы несовместимых высказываний.
2. Представить в ССФ предикат  .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 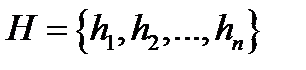 и утверждения и утверждения 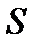 , доказать справедливость выражения , доказать справедливость выражения 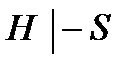 . .
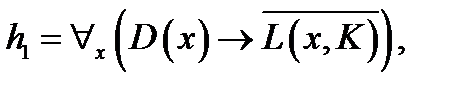 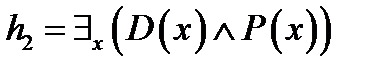
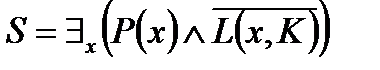 .
4. Найти функцию .
4. Найти функцию 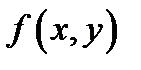 , полученную из функций , полученную из функций 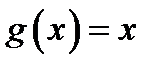 и и 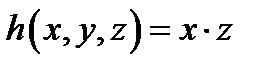 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 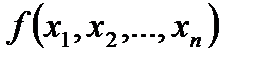 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 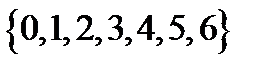 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Умозаключения.
2. Представить в ССФ предикат 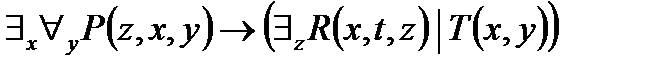 .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 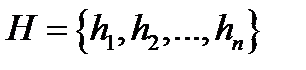 и утверждения и утверждения 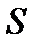 , доказать справедливость выражения , доказать справедливость выражения 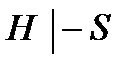 . .
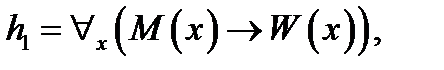 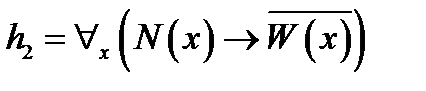 , ,
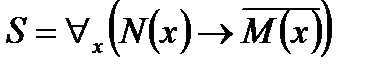 .
4. Найти функцию .
4. Найти функцию 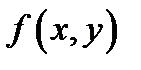 , полученную из функций , полученную из функций 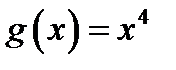 и и 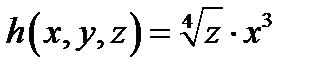 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 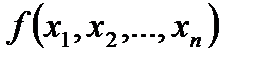 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 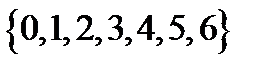 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||||
1. Критерий правильности дедуктивных умозаключений.
2. Представить в ССФ предикат 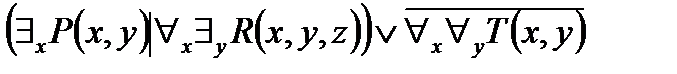 .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез .
3. Используя метод резолюций для предикатных выражений для заданного множества гипотез 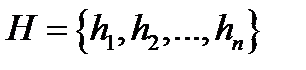 и утверждения и утверждения 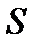 , доказать справедливость выражения , доказать справедливость выражения 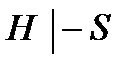 . .
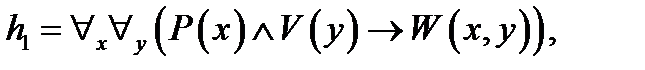 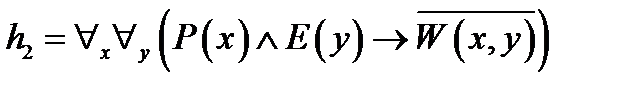 , ,
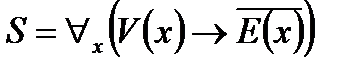 .
4. Найти функцию .
4. Найти функцию 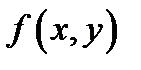 , полученную из функций , полученную из функций 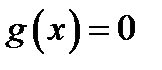 и и 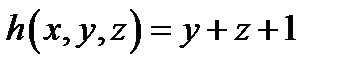 по схеме примитивной рекурсии.
5. Написать формулу числовой функции по схеме примитивной рекурсии.
5. Написать формулу числовой функции 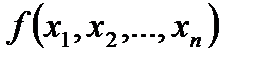 , вычислимой машиной Тьюринга с множеством внутренних состояний , вычислимой машиной Тьюринга с множеством внутренних состояний 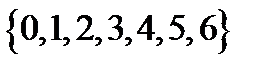 , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой. , где 0 – заключительное, а 1 – начальное состояния, если машина задана своей программой.
|
Форма №20А
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 10
 МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Московский государственный технический университет радиотехники, электроники и автоматики"
МГТУ МИРЭА
| Кафедра: ОНД | УТВЕРЖДАЮ Зав. кафедрой | |||||||||||||||||||||
| Дисциплина: «Математическая логика и теория алгоритмов» Форма обучения: очно-заочная | Дата: | ||||||||||||||||||||||
1. Анализ рассуждений при помощи таблиц истинности. Проанализировать рассуждение 2. Представить в ССФ предикат 3. Используя метод резолюций для предикатных выражений для заданного множества гипотез
4. Найти функцию 5. Написать формулу числовой функции
|
Форма №20А





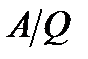
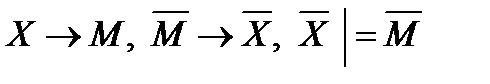 при помощи таблицы.
при помощи таблицы.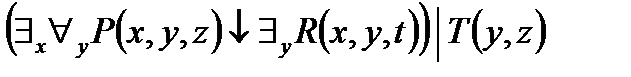 .
.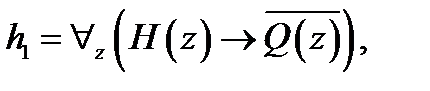
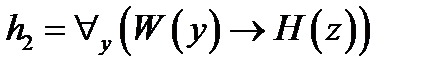 ,
,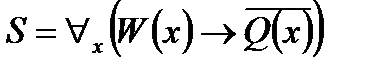 .
.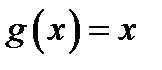 и
и 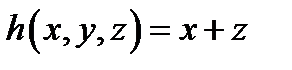 по схеме примитивной рекурсии.
по схеме примитивной рекурсии.
