ЛАБОРАТОРНАЯ РАБОТА № 3
«ПОСЛЕДОВАТЕЛЬНАЯ RC-ЦЕПЬ
ПРИ ВОЗДЕЙСТВИИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ»
Выполнила: Маругина К. А.
Группа: ЭР-16-15
Бригада №7
Проверил: Фланден В. С.
Москва 2016
ЛАБОРАТОРНАЯ РАБОТА № 3
Цель работы — на простейших примерах освоить основные понятия и методы анализа линейной цепи при гармонических колебаниях.
Изучаются следующие основные вопросы:
1) понятие комплексной амплитуды гармонического колебания; 2) комплексный метод анализа линейной цепи при гармонических колебаниях; 3) поведение простейшей нерезонансной цепи (последовательной RC -цепи) при воздействии гармонических колебаний; 4) векторная диаграмма изучаемого процесса; 5) правила вычисления эквивалентной емкости при параллельном и последовательном соединении элементов.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Представление о гармонических колебаниях:
Если некоторая величина u(t) изменяется во времени по закону
u(t) = umcos(ωt + φ), (1.1)
то говорят, что происходят гармонические колебания,причем ит называется амплитудой,ω— круговой частотой,а аргумент косинуса ωt + φ – фазойколебаний (полной фазой); последняя, если это требуется, приводится к значению, лежащему в пределах 0 ÷ 2π; или –π ÷ π; величину φ называют начальной фазой (а также фазовым сдвигом или просто фазой).
Метод комплексных амплитуд:
Перейдём к изложению обычно используемого в случае гармонических колебаний метода комплексных амплитуд. На основании известной формулы Эйлера функцию и (1.1) можно представить как вещественную часть экспоненциальной:
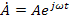, (1.2)
где множитель A называется комплексной амплитудой колебаний. Как видно, в комплексном представлениимы имеем произведение функции координат и функции времени.
Комплексное сопротивление Z представляет собой отношение комплексных амплитуд напряжения и тока:
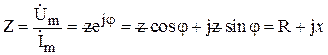(1.3)
RC-цепь — электрическая цепь, состоящая из конденсатора и резистора. Её можно рассматривать как делитель напряжения с одним из плеч, обладающих ёмкостным сопротивлением переменному току.
RC-цепи пропускают постоянную составляющую сигнала, отсекая высокие частоты, то есть являются фильтрами нижних частот. При этом, чем выше постоянная времени{\displaystyle \tau }, тем ниже частота среза. В пределе пройдёт только постоянная составляющая.
У CR-цепей входной сигнал идёт на конденсатор, а выходной снимается с резистора. Для постоянного напряжения конденсатор представляет собой разрыв цепи, то есть постоянная составляющая сигнала в цепи дифференцирующего типа будет отсечена.
Такие цепи являются фильтрами верхних частот. И частота среза в них определяется всё той же постоянной времени{\displaystyle \tau }. Чем больше постоянная времени{\displaystyle \tau }, тем ниже частота, которая может быть без изменений пропущена через цепь.
ДОМАШНЯЯ ПОДГОТОВКА
Схемы изучаемых цепей
| uвх |
| uC |
| uR |
| R |
| C |
| uC |
| uR |
| R |
| C |
| б) |
| а) |
| uвх |
Рис.1
На (рис. 1, а)выходное напряжение снимается с конденсатора, на (рис. 1, б) – с резистора.
Основные формулы
Входное гармоническое напряжение:
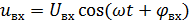(1.4)
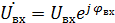(1.5)
Выходное напряжение на конденсаторе:
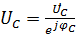(1.6)
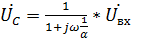(1.7)
Выходное напряжение на резисторе:
(1.8)
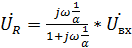(1.9)
Начальная фаза напряжения на конденсаторе:
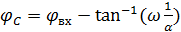(1.10)
Начальная фаза напряжения на резисторе:
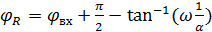(1.11)
Коэффициент затухания цепи:
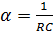(1.12)
Расчетная часть
Дано: Uвх=1 В; φвх=0°
C1=1/(2ωR)
C2=1/(ωR)
C3=2/(ωR)
Для случая с последовательными конденсаторами:
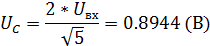
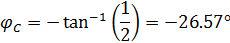
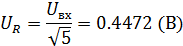
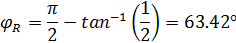
Для случая с одним конденсатором:
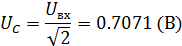
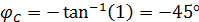
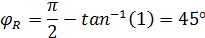
Для случая с параллельными конденсаторами:
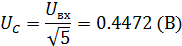
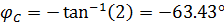
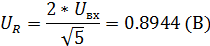
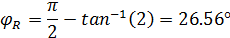
Построение векторных диаграмм
Для случая 1:
Для случая 2:
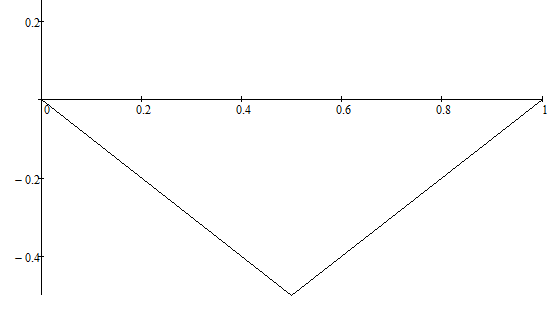
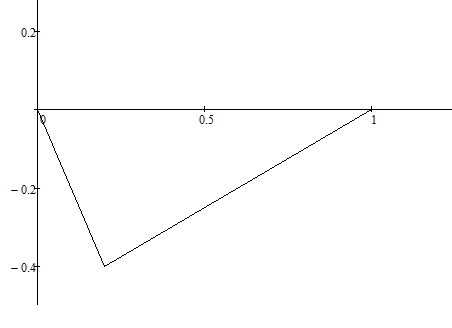
Для случая 3:
Построение осциллограмм
Для случая 1:
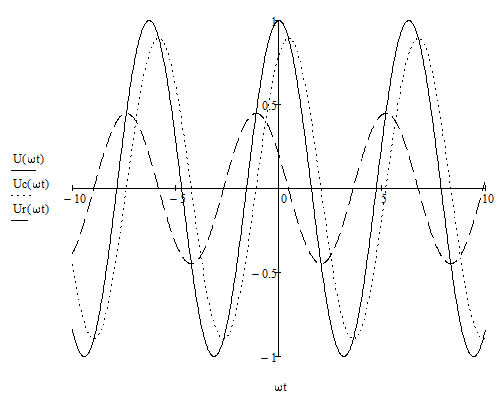
Для случая 2:
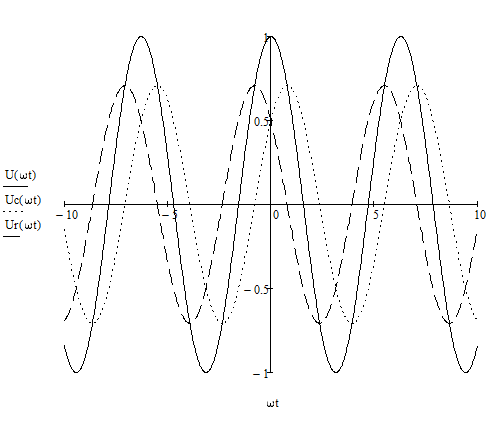
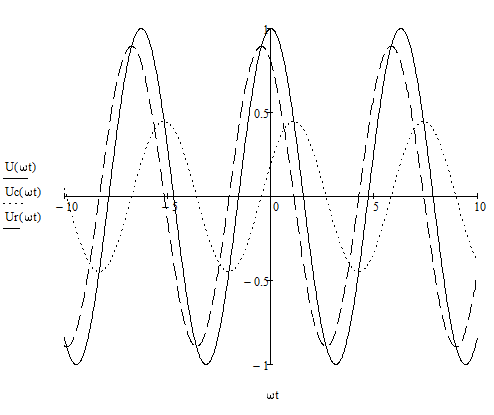
Для случая 3:
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
3.1. Включили блок питания лабораторной установки.
3.2. Собрали исследуемую цепь и установили требуемые значения.
3.3. Измерили напряжения на резисторе и конденсаторе, также измерили начальную фазу.
3.4. Сравнили полученные путем измерений значения с результатами расчетов.
Таблица №1
| C | UC, В | UR, В | j C, гр. | j R, гр. | Примечания |
| Одиночный элемент | 0,7071 | 0,7071 | -45 | Расчет | |
| 0,69 | 0,685 | -51,6 | 43,2 | Измерение | |
| Параллельное соединение | 0,4472 | 0,8944 | -63,43 | 26,56 | Расчет |
| 0,465 | 0,89 | -68,51 | 25,66 | Измерение | |
| Последовательное соединение | 0,8944 | 0,4472 | -26,57 | 63,42 | Расчет |
| 0,905 | 0,435 | -20,86 | 59,47 | Измерение |
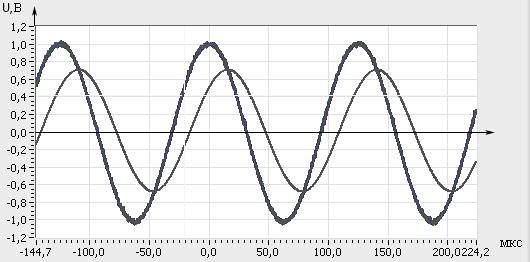
График 1: измерения с конденсатора (одиночный).
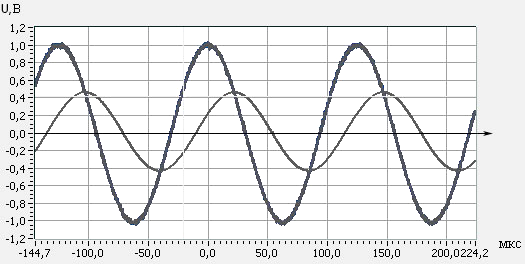
График 2: измерения с конденсатора (параллельное соединение).
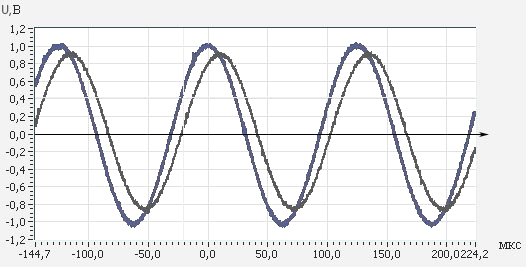
График 3: измерения с конденсатора (последовательное соединение).
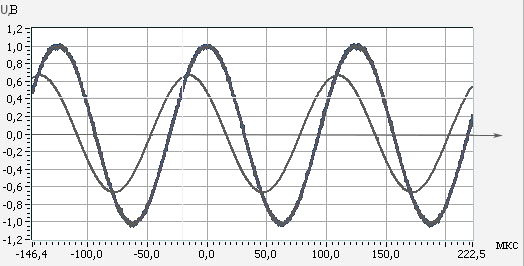
График 4: измерения с резистора (одиночный).
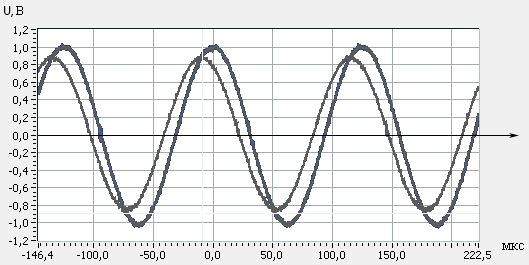
График 5: измерения с резистора (параллельное соединение).
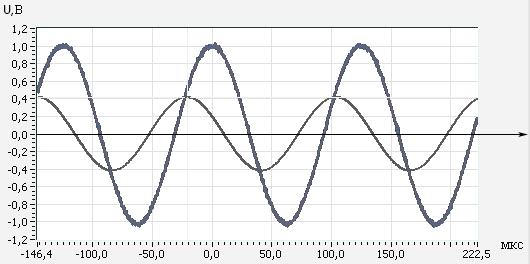
График 6: измерения с резистора (последовательное соединение).
Вывод:
Исходя из экспериментальных и расчетных данных, видна зависимость амплитуды и смещения фазы гармонического сигнала от типа и количества элементов, с которых снимается напряжение. При детальном рассмотрении полученных данных становится понятно, что при снятии напряжения с резистора фаза смещается вправо (при возрастании сопротивления смещение увеличивается), при снятии напряжения с конденсатора фаза смещается влево (при возрастании емкости смещение увеличивается).
