Приведение матричной игры к задаче линейного программирования.

Обозначим через S_A=(p₁, p₂, …, p_n) оптимальную смешанную стратегию игрока A. Требуется найти вероятности и определить цену игры при условии, что известна платёжная матрица игры. Допустим, что игрок B выбирает чистую стратегию B₁. Тогда средний выигрыш для игрока A будет равен a₁₁p₁+a₂₁p₂+…+a_n1p_n. Этот выигрыш должен быть не меньше цены игры v, следовательно, a₁₁p₁+a₂₁p₂+…+a_n1p_n≥v.
Если игрок B выберет стратегию B₂, то и в этом случае средний выигрыш игрока A должен быть не меньше цены игры v, следовательно, a₁₂p₁+a₂₂p₂+…+a_n2p_n≥v.
Какую бы стратегию ни выбирал игрок B, выигрыш игрока A всегда должен быть не меньше цены игры v. Поэтому мы можем записать следующую систему из m неравенств (напоминаем, что m — число чистых стратегий игрока B):
a ₁₁p₁+a₂₁p₂+…+a_n1p_n≥v;

a₁₂p₁+a₂₂p₂+…+a_n2p_n≥v;
………………………… (1)
a_1mp₁+a_2mp₂+…+a_nmp_n≥v.
При этом p₁+p₂+…+p_n=1. (2) Введя обозначения x₁=p₁/v, x₂=p₂/v, … x_n=p_n/v, перепишем (1) и (2) в виде
a ₁₁x₁+a₂₁x₂+…+a_n1x_n≥1;

a₁₂x₁+a₂₂x₂+…+a_n2x_n≥1;
………………………… (3)
a_1mx₁+a_2mx₂+…+a_nmx_n≥1;
x₁+x₂+…+x_n=1/v. (4)

Нам желательно, чтобы цена игры была максимальной, следовательно, 1/v должна быть минимальной. Таким образом, поиск оптимальной смешанной стратегии свёлся к решению следующей задачи линейного программирования: надо найти неотрицательные величины x_i такие, чтобы они удовлетворяли неравенствам (3) и обращали в минимум сумму x₁+x₂+…+x_n, т.е.
L= x₁+x₂+…+x_n→min, при ограничениях
a ₁₁x₁+a₂₁x₂+…+a_n1x_n≥1;

a₁₂x₁+a₂₂x₂+…+a_n2x_n≥1;

…………………………
a_1mx₁+a_2mx₂+…+a_nmx_n≥1; x_i≥0, i=1, 2, …, n/

36. Примеры использования аппарата позиционных игр в экономике.*????

Предположим следующую ситуацию. На рынке некоторого про­дукта доминирует производитель-монополист (Фирма 1), и моно­польное положение приносит ему 12 млрд. руб. прибыли. Высокая прибыль в данном секторе привлекает других производителей, и, в частности, Фирма 2 решает вопрос: построить ли ей свой завод и начать на нем производство такого же товара? Однако ей известно, что Фирма 1 может предпринять некоторые действия в ответ на вторжение. С одной стороны, Фирма 1 может снизить объем своего производства, уступая часть рынка Фирме 2 и деля с ней получае­мую прибыль — так, как это происходило в примере поведения фирм-олигополистов. В этом случае каждая из фирм получит по 6 млрд. руб. прибыли. С другой стороны, Фирма 1 может сохранить объем своего производства. В этом случае рост совокупного предло­жения товара Фирмами 1 и 2 снизит цену на этот товар, и, как следствие, прибыль Фирмы 1 упадет до 5 млрд. руб. Одновременно снижение цен приведет к тому, что Фирма 2, сделавшая предвари­тельные затраты для выхода на новый для нее рынок, понесет чис­тые убытки: она потеряет на этом деле 2 млрд. руб. В случае, если Фирма 2 воздерживается от вступления на рынок, она ничего не выигрывает и не проигрывает (ее прибыль равна 0 млрд. руб.), а Фирма 1 продолжает получать монопольную прибыль в 12 млрд. руб. Если же Фирма 1 вдруг решит в этой ситуации снизить объем своего производства, ее прибыль упадет до 8 млрд. руб.

В принципе сформулированная конечная неантагонистическая игра двух лиц может быть описана следующей матрицей выигрышей (пер­выми указаны выигрыши Фирмы 1 в млрд. руб.):

Стратегия Фирмы 1

Стратегия Фирмы 2

Вступить Воздержаться

Однако заметим, что описанная игра по своим условиям отлича­ется от уже рассмотренных игр. Если ранее мы предполагали, что игроки принимают свои решения одновременно, не зная о решении партнера (что было весьма существенно!), то в данной игре Фирма 1 принимает решение, уже зная о решении, избранном Фирмой 2, в ответ на действия Фирмы 2, и это в корне меняет ситуацию.

Игры подобного типа, где задается последовательность приня­тия решений игроками, называются позиционными играми; число игроков и шагов в них может равняться 2 (как в нашем примере), 3 и т. д. К позиционным многошаговым играм двух лиц, где игроки принимают решения, зная о всех предыдущих решениях партнера, можно отнести, например, шахматы и шашки.

Сохранить объем Снизить объем производства производства

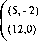
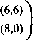
В силу отмеченных особенностей структуры позиционной игры ее более наглядно представляет не матрица выигрышей, а дерево решений (или, в общем случае, граф решений), приводящее игроков из исходной позиции в конечные. Так, описанную игру Вступление на рынок можно представить следующим деревом (рис. 13.9), ветви которого соответствуют решениям партнеров, а у каждой из вися­чих вершин указаны выигрыши игроков (как и ранее, первыми указаны выигрыши Фирмы 1, в млрд. руб.).

Рисунок 13.9. Дерево решений для игры Вступление на рынок

Вершины дерева игры называются позициями; позиции, непо­средственно следующие за некоторой позицией, называются аль­тернативами’, позиции, не имеющие альтернатив, называются окон­чательными, а ведущие в них пути — партиями (так, описанная игра имеет четыре партии). Часть дерева решений, описывающая игру из некоторой позиции после нескольких начальных шагов партнеров, называется подыграй, и се решение может представлять самостоя­тельную задачу. (Хорошим примером подыгр являются шахматные этюды типа "За сколько шагов из данной позиции белые смогут поставить мат черному королю?")

Описанная игра Вступление на рынок имеет две пары стратегий (две партии), удовлетворяющих условию равновесия по Нэшу: парт­ия, когда Фирма 2 решает воздержаться от вступления на рынок, а Фирма I сохраняет объем своего производства, и партия, когда Фирма 2 решает вступить на рынок, а Фирма 1, в свою очередь, снижает объем производства. Легко убедиться, что в каждой из этих двух партий отступление каждого из игроков от своей стратегии приво­дит к уменьшению его выигрыша.