Метод рационализации при решении показательных и логарифмических неравенств
ВВЕДЕНИЕ
В предыдущей статье мы подробно рассмотрели методы решения рациональных и дробно-рациональных неравенств. В основе этих методов лежит очевидный факт: непрерывная функция на отрезке между двумя нулевыми значениями не изменяет знак (положительна или отрицательна). Некоторые элементарные свойства многочленов, связанные с понятием кратного корня, позволяют быстро установить знак дробно-рациональной функции на каждом таком интервале монотонности. Заметим, что в общем случае требуется вычислять значения функции в «пробных» точках на каждом интервале, что более трудоемко.
В этой статье мы рассмотрим примеры сведения логарифмических и показательных неравенств, у которых основание, выражение под знаком логарифма, степень – многочлены. Оказывается, такие неравенства эффективно сводятся к дробно-рациональным или рациональным, причем (что важно, например, на ЕГЭ) полученные решения будут более компактными по сравнению с традиционными.
Сведение логарифмического неравенства к системе рациональных неравенств
Рассмотрим логарифмическое неравенство вида
, (1)
где 
- некоторые функции (об их природе будем говорить ниже).
Стандартный метод решения такого неравенства предполагает разбор двух случаев на области допустимых значений неравенства.
В первом случае, когда основания логарифмов удовлетворяют условию
, знак неравенства обращается: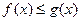 
.
Во втором случае, когда основание удовлетворяет условию 
, знак неравенства сохраняется: 
.
На первый взгляд – все логично, рассмотрим два случая и потом объединим ответы. Правда, при рассмотрении второго случая возникает определенный дискомфорт – приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос – можно ли все это как-нибудь рационализировать объединить?
Ответ на этот вопрос содержится в следующей теореме.
Теорема 1. Логарифмическое неравенство
равносильно следующей системе неравенств:
(2)
Доказательство. Начнем с того, что первые четыре неравенства системы (2) задают множество допустимых значений исходного логарифмического неравенства. Обратим теперь внимание на пятое неравенство. Если , то первый множитель этого неравенства будет отрицателен. При сокращении на него придется изменить знак неравенства на противоположный, тогда получится неравенство 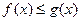. Если же , то первый множитель пятого неравенства положителен, сокращаем его без изменения знака неравенства, получаем неравенство . Таким образом, пятое неравенство системы включает в себя оба случая предыдущего метода. Терема доказана.
Пример. Решить неравенство
.
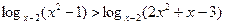Решение. Воспользуемся теоремой 1. получим следующую систему неравенств:
Решая первые четыре неравенства, практически находим ОДЗ исходного неравенства:
Откуда: 
.
Решим теперь пятое неравенство системы. После элементарных преобразований получим неравенство
.
Умножим второй сомножитель на -1 и поменяем знак неравенства:
.
Нетрудно заметить, что корнями второго множителя в этом неравенстве являются числа 1 и -2. Поэтому, раскладывая второй множитель на одночлены первого порядка, получаем:
.
Это неравенство легко решить методом интервалов: 
.
С учетом найденного ранее ОДЗ, получаем окончательный ответ.
Ответ: 
.
Замечание. Обращаем внимание тех, кто собирается применять метод рационализации на ЕГЭ на следующее: критерии проверки таковы, что при ошибочном решении, но правильно найденном ОДЗ (при дополнительных условиях) можно получить балл. Поэтому рекомендуется сначала отдельно найти ОДЗ, а затем перейти к решению основного (пятого) неравенства.
