Пусть задана система линейно-алгебраических уравнений неизвестное  разрешенное, если какое-нибудь уравнение этой системы содержит
разрешенное, если какое-нибудь уравнение этой системы содержит  с коэффициентом равным 1, а остальные уравнения эту неизвестную не содержат.
с коэффициентом равным 1, а остальные уравнения эту неизвестную не содержат.
Система разрешенная, если каждое уравнение содержит разрешенную неизвестную.
10. Симплекс метод. (Храмова)
Симплексный метод – это метод целенаправленного перебора опорного решения задач линейного программирования (з.л.п).
Заметим, что опорные решения – это угловая точка многогранника.
Симплексный метод включает в себя:
1. Нахождение начального опорного решения;
2. Способ перехода от одного опорного решения к другому, на котором целевая функция ближе к оптимальности;
3. Критерий оптимальности (этот критерий позволяет остановить поиск решений).
1. Предполагая, что заданная запись в канонической форме, т.е. в форме равенств:
F(x) = c1x1 + …+ cnxn → max
a11x1+a12x2+…+a1nxn=b1
a21x1+a22x2+…+a2nxn=b2
am1x1+am2x2+…+amnxn=bn
Для нахождения начального опорного решения применяем метод Гаусса и приводим систему ограничений к разрешенной системе.
После приведения к разрешенной системе получим:
x1+ … a1m+1xm+1+… a1kxk+… a1nxn=b1
x2+… a2m+1xm+1+… a2kxk+ … a2nxn=b2
xm+ amm+1xm+1+… amkxk+… 2mnxn=bm
Ā1= (10...0), Ā2=(01..0), Ām=(00..1)
X1= (x1,x2,x3)
X1= (b1,b2,bm)
Можно доказать, что эти вектора независимы, таким образом мы выясним, как найти начальное опорное решение.
2. Возьмем столбец с номером k и на этом столбце выберем aek (разрешенный элемент)
Применим метод Жордана:
а) Делим строку L на aek
b'e = be/ aek,треб.aek>0
b) далее получаем 0 для другого элемента этого столбца
b'i = bi – be/aek * aik ≥0 => bi/aik ≥be/aek.
Из этого неравенства выводим критерий выбора е, при условии, что знаем как выбрать k
min= bi/aik
Рассмотрим способ выбора столбца k.
Для этого 1-ое решение будем сравнивать с новым 2-ым решением.
F(X2)= Ʃ cibi – be/aek (Ʃ ciaik – ck)
Обозначаем Ѳk= be/aek
∆k = Ʃ ciaik – ck
Называется оценкой разложения вектора услов. Ak по базису опорного решения.
F(X2) = F(X1)- Ѳk*∆k
Если оценка меньше 0 (∆k < 0), то отсюда вывод:
Утверждение 1. Если в з.л.п. хотя бы для одного вектора условий оценка разложений отрицательная, то опорное решение может быть улучшено!
Утверждение 2. Критерий выбора k: выбираем из условий max{-Ѳk*∆k}, другими словами, перебираем все отрицательные оценки и берем наибольшее значение по модулю.
Утверждение 3. Опорное решение является оптимальным, если все оценки не отрицательны.
Оптимальное решение является единственным, если для любого вектора условий, не входящего в базис, оценка отлична от 0.
11. Пример решения задач линейного программирования симплекс методом. (Барыгина)
Для того, чтобы решить задачу симплексным методом необходимо выполнить следующее:
Привести задачу к каноническому виду
Найти начальное опорное решение с "единичным базисом" (если опорное решение отсутствует, то задача не имеет решение ввиду несовместимости системы ограничений)
Вычислить оценки разложений векторов по базису опорного решения и заполнить таблицу симплексного метода
Если выполняется признак единственности оптимального решения, то решение задачи заканчивается
Если выполняется условие существования множества оптимальных решений, то путем простого перебора находят все оптимальные решения
Пример решения задачи симплексным методом
Пример 26.1
Решить симплексным методом задачу:

Решение:
Приводим задачу к каноническому виду.
Для этого в левую часть первого ограничения-неравенства вводим дополнительную переменную x6 с коэффициентом +1. В целевую функцию переменная x6 входит с коэффицентом ноль (т.е. не входит).
Получаем:

Находим начальное опорное решение. Для этого свободные (неразрешенные) переменные приравниваем к нулю х1 = х2 = х3 = 0.
Получаем опорное решение Х1 = (0,0,0,24,30,6) с единичным базисом Б1 = (А4, А5, А6).
Вычисляем оценки разложений векторов условий по базису опорного решения по формуле:
Δk = CбXk — ck
Где:
Cб = (с1, с2,..., сm) — вектор коэффициентов целевой функции при базисных переменных
Xk = (x1k, x2k,..., xmk) — вектор разложения соответствующего вектора Ак по базису опорного решения
Ск — коэффициент целевой функции при переменной хк.
Оценки векторов входящих в базис всегда равны нулю. Опорное решение, коэффиценты разложений и оценки разложений векторов условий по базису опорного решения записываются в симплексную таблицу:

Сверху над таблицей для удобства вычислений оценок записываются коэффициенты целевой функции. В первом столбце "Б" записываются векторы, входящие в базис опорного решения. Порядок записи этих векторов соответствует номерам разрешенных неизвестных в уравнениях ограничениях. Во втором столбце таблицы "Сб" записываются коэффициенты целевой функции при базисных переменных в том же порядке. При правильном расположении коэффициентов целевой функции в столбце "Сб" оценки единичных векторов, входящих в базис, всегда равных нулю.
В последней строке таблицы с оценками Δk в столбце "А0" записываются значения целевой функции на опорном решении Z(X1).
Начальное опорное решение не является оптимальным, так как в задаче на максимум оценки Δ1 = -2, Δ3= -9 для векторов А1 и А3 отрицательные.
По теореме об улучшении опорного решения, если в задаче на максимум хотя бы один вектор имеет отрицательную оценку, то можно найти новое опорное решение, на котором значение целевой функции будет больше.
Определим, введение какого из двух векторов приведет к большему приращению целевой функции.
Приращение целевой функции находится по формуле:

Вычисляем значения параметра θ01 для первого и третьего столбцов по формуле:
Получаем θ01 = 6 при l = 1, θ03 = 3 при l = 1 (таблица 26.1).
Находим приращение целевой функции при введении в базис первого вектора ΔZ1 = — 6*(- 2) = 12, и третьего вектора ΔZ3 = — 3*(- 9) = 27.
Следовательно, для более быстрого приближения к оптимальному решению необходимо ввести в базис опорного решения вектор А3 вместо первого вектора базиса А6, так как минимум параметра θ03 достигается в первой строке (l = 1).
Производим преобразование Жордана с элементом Х13 = 2, получаем второе опорное решение Х2 = (0,0,3,21,42,0) с базисом Б2 = (А3, А4, А5). (таблица 26.2)

Это решение не является оптимальным, так как вектор А2 имеет отрицательную оценку Δ2 = — 6. Для улучшение решения необходимо ввести вектор А2 в базис опорного решения.
Определяем номер вектора, выводимого из базиса. Для этого вычисляем параметр θ02 для второго столбца, он равен 7 при l = 2. Следовательно, из базиса выводим второй вектор базиса А4. Производим преобразование Жордана с элементом х22 = 3, получаем третье опорное решение Х3 = (0,7,10,0,63,0) Б2 = (А3, А2, А5) (таблица 26.3).

Это решение является единственным оптимальным, так как для всех векторов, не входящих в базис оценки положительные
Δ1 = 7/2, Δ4 = 2, Δ6 = 7/2.
Ответ: max Z(X) = 201 при Х = (0,7,10,0,63).
12. Двойственные задачи. (Проторгуева)
Пусть дана задача линейного программирования
F(x) = c1x1 + … + cmxn → max
а11х1 + а12х2 + … + сm1хn ≤ в1
а21х1 + а22х2 + … + сm2хn ≤ в2
....
аm1х1 + аm2х2 + … + сmnхn ≤ вm
Двойственной задачей является задача
Ζ (Y)= в1у1 + в2у2 + … + вmуm → min
а11у1 + а12у2 + … + сm1уn ≥ с1
а21у1 + а22у2 + … + сm2уn ≥ с2
….
аn1у1 + аn2у2 + … + сmnуn ≥ сm
yj ≥0, j = 1, 2 … m
y1, y2…ym – неизвестные двойственной задачи
Неизвестных в двойственной задачи столько, сколько ограниченных неравенств в двойственной задачи. Соответствующее число ограниченной двойственной задачи равно числу неизвестной двойственной задачи. Если матрицу обозначить через (А). Если одна из пары двойственной задачи имеет оптимальное решение, то двойственная задача так же имеет оптимальное решение, причём значение целевых функций на оптимальном решении совпадают.
Если одна из задач не имеет решения, то так же не имеет решения и двойственная задача. Это утверждение позволяет сводить задачи на min, max.
Пример:
Ζ (x) = 6x1 + 7х2 + 9x3 → min
1х1 + 2х2 + 3х3 ≥ 5
1х1 + 1х2 + 1х3 ≥2
1х1 + 2х2 + 6х3 ≥7
Х1≥0; Х2≥0; Х3≥0
F(Y)= 5у1 + 2у2 + 4у3 → max
A = 
AT = 
1у1 + 2у2 + 1у3 ≤ 6
2у1 + 1у2 + … + 2у3 ≤ 7
3у1 + 1у2 + 6у3 ≤ 9
Формулы вычисления среднего выигрыша
Чтобы найти средние или математические ожидания нужно каждое значение случайной величины умножить на соответствующую вероятность и результат сложить. Значению aij соответствующей вероятности рi, qj
aij соответствующая вероятность рi, qj; НА(Р,Q)
НА(Р,Q) =  (для первого)
(для первого)
НB(Р,Q) =  (для второго)
(для второго)
13. Биматричные игры. Биматричные игры 2х2. (Никонов)
Вначале мы изучали игры с природой, а затем антагонистические игры. В антагонистических играх участники преследуют прямо противоположные интересы. В таких играх платежная матрица описывает выигрыш одного игрока, в тоже время проигрыш второго игрока. В реальности встречаются конфликты более общего характера. В них участники преследуют различные, но не обязательно противоположные интересы. И поскольку интересы не обязательно противоположны, то их поведение является более разнообразным.
Такие игры в свою очередь разделяют на 2 вида:
- бескоалиционные (некооперативные)
- кооперативные
В бескоалиционных играх исключается сотрудничество между игроками, игроки принимают решения независимо друг от друга. А в кооперативных играх до начала игры игроки образуют коалиции и принимают взаимо-обязывающие соглашения о своих стратегиях.
Некооперативные игры далее будем называть (Биматричными)
Биматричная игра – подобна антагонистической игре и задается платежной матрицей, но теперь каждому игроку принадлежит своя матрица. Пусть игрок А имеет m стратегий [А1..А2…Аm], тогда игрок В имеет n стратегий [В1..В2..Вn].
Если игрок В применяет стратегию i, тогда игрок А применяет стратегию j, то в результате первый игрок получит выигрыш Аij а второй игрок получит выигрыш Вij. Общий вид платежных матриц игроков:
Платежная матрица игрока А
| В1 | В2 | … | Вn | |
| A1 | A11 | A12 | … | A1n |
| A2 | A21 | A22 | … | A2n |
| … | … | … | … | … |
| Am | Am1 | Am2 | … | Amn |
Платежная матрица игрока В
| В1 | В2 | … | Вn | |
| A1 | B11 | B12 | … | B1n |
| A2 | B21 | B22 | … | B2n |
| … | … | … | … | … |
| Am | Bm1 | Bm2 | … | Bmn |
Постановка задачи
Как и в антагонистических играх, требуется найти смешанные стратегии, которые являются оптимальными, т.е. необходимо найти вероятность:
Р1- частота принятия стратегии А1
Р2- частота принятия стратегии А2
Р3- частота принятия стратегии А3
Все эти величины положительны и их сумма = 1. 
Аналогично и для игрока В:
q1- частота принятия стратегии B1
q2- частота принятия стратегии B2
q3- частота принятия стратегии B3
Все эти величины также положительны и их сумма = 1. 
Формулы вычисления средних выигрышей
Что бы найти среднее и максимальное значение, нужно каждое значение величины умножить на вероятность и результат сложить.
Аij – соответствует вероятность Рi x qi
Отсюда:
Ha (P,Q) = 
НB (P,Q) = 
Биматричная игра 2х2
| А11 | А12 |
| А21 | А22 |
А=
| B11 | B12 |
| B21 | B22 |
В =
Р – частота применения 1 игроком стратегии (А1)
1-Р – частота применения стратегии (А2)
q – частота применения стратеги (В1)
1- q – частота применения стратегии (В2)
Формулы
На (р, q); Нв (р, q)
1. На (р, q) = а11*(р q) + р(1- q) + а21*(1-р)q + а22*(1-р)(1- q)
На = (а11-а12-а21+а22)р q + (а12-а22)р + (а21-а22)* q + а22
3. Нв = (в11-в12-в21+в22)р q + (в12-в22)р + (в21-в22)* q + в22
Введем следующие обозначения:
С = А11- А12- А21+А22
D = B11- B12- B21+B22
α = A22-A12
β = B22-B21
Ɣ = А21-А22
Δ = B12-B22
Ha(p;q) = C*(pq) – αp+ Vq +A22
(*)
Hb(p;q) = D*(pq) – Δ p + βq + B22
Раздел II.
Определение: Пара чисел р* и q*, 0≤ р*≤ 1; 0 ≤ q*≤1.
Определим равновесие, если выполнены 2 условия;
1. (Неравенство)
1.1 На (рq) < Ha(p*,q*) Ɣ p ϵ [0;1]
1.2 HB(p*q) ≤ HB(p*q*)
где, На (средний выигрыш 1 го игрока)
НВ (средний выигрыш 2 го игрока)
Неравенство (1) означает стратегии (p*q*) – определяем равновесие, если отклонение одного из игроков или условие, что другой игрок сохраняет свой выбор приводит к тому, что выигрыш относившегося игрока только уменьшается, таким образом, отклонение от равновесия не выгодно самому игроку.
Теорема 1. (Дж.Неш)
Всякая биматричная игра имеет хотя бы одну точку равновесия, без доказательства.
Теорема 2. Выполнение неравенства (1) равносильно выполнению неравенств:
Неравенство 2.
На(0,q) ≤ Ha (p*q*)
Ha(1,q) ≤ Ha (p*q*)
Неравенство 3.
НB(p*,0) ≤ HB (p*q*)
HB(p*,1) ≤ HB (p*q*)
Неравенство 2 означает, что неравенство 1.1 достаточно проверить для двух крайних значений (когда р=0 и р=1).
Точнее говоря для чистых стратегий. Аналогично неравенство 3, это проверка неравенства 1.2 для чистых стратегий. Для нахождения точки равновесия будем решать неравенство (2 и 3) для этого воспользуемся формулой (*) Согласно этому представлению:
Ha(p*,q*) = Ср*q*-2p*+ Ɣq* + a22 (4)
Ha(0,q*) = Ɣq* + a22 (5)
Ha(1,q*) = Cq*- α + Ɣq* + a22 (6)
Первое неравенство (2) имеет вид:
Ha(p*,q*) - На(0,q*)≥0
или с учетом (4) и (5)
р*(Сq*- α) ≥0 (7)
Второе неравенство (2) имеет вид:
Ha(p*,q*) - На(1,q*)≥0
или с учетом (4) и (5)
Ср*q* - αp* - (Cq*- α) ≥0
= Cq*-(p*-1) – α(p*-1) ≥0 (8)
Неравенство (8):
(р*-1)(Сq*- α) ≥0
p*(Cq*- α) ≥0 (9)
Аналогично решим неравенство (3)
Нв(p*q*) = Dp*q*- βq*+ Δ p + βq + B22 (10)
HB(p*q*) = Δ p+ B22 (11)
HB=(p*,1) = Dp*- β+ Δ p* + βq + B22 (12)
Первое неравенство (3)
14. Нв(р*,0) ≤ Нв(р*,q*)
Dp*q*- βq*≥0
q*(Dp*- β)≥0
Второе неравенство (3)
HB(p*q*) – HB (p*,1) ≥0
Учитывая (10) и (12)
Dp*q* - βp*-(Dp*-β) = p* x D(q*-1)- β(q*-1) ≥0
(q*-1)(Dp*- β) ≥0
q*(Dp*- β) ≥0
15. Алгоритм решения биматричной игры.( Куинь)
Задача состоит в том, что найти p, 1-p, 0≤p≤1 и q, 1-q, 0≤q≤1
Определение: пара чисел p* и q*, 0≤ p* ≤1 и 0≤ q* ≤1 определяет равновесную ситуацию (равновесие), если выполнены два условия:
 (1)
(1)
Неравенство (1) означает стратегия  определяет равновесие если отношение от нее от одного из игроков при условии, что они сохраняют свой выбор приводит к тому, что выигрыш, отклонивший свои игрока может уменьшиться. Таким образом, отклонение от равновесия не выгодно для игроков.
определяет равновесие если отношение от нее от одного из игроков при условии, что они сохраняют свой выбор приводит к тому, что выигрыш, отклонивший свои игрока может уменьшиться. Таким образом, отклонение от равновесия не выгодно для игроков.
Теорема 1: (Дж. Нэш)
Всякая биматричная игра имеет хотя бы одну точку равновесия. (без доказательства)
Теорема 2:
Выполнение неравенства (1) равносильно выполнению неравенств:
 (2)
(2)
 (3)
(3)
(без доказательства)
Неравенство (2) означает, что неравенство (1а) достаточно проверить для двух крайних значений, когда p=0 и q=1. Точнее говоря для чистых стратегий. Аналогично, неравенство (3) – проверка неравенства (1b) для чистых стратегий.
Для нахождения точки равновесия будем решать неравенства (1) и (3). Для этого будем воспользоваться представление:
 (*)
(*)
Согласно с (*)
H(A) (0, q*) = α × q* + a22 (4)
H(A) (1, q*) = C × q*– α + γ × q*+a22 (5)
Первое неравенство (2) имеет вид:
H(A) (p*,q*) – H(A) (0,q*) ≥ 0
Или с учетом (*) и (4)
p* (C × q*– α) ≥ 0 (6)
Второе неравенство (2) перепишем в виде:
H(A) (p*,q*) – H(A) (1,q*) ≥ 0
Или с учетом (*) и (4)
C× p*× q* – α × p*– (C × q*– α) ≥ 0
C × q*(p*–1) – α (p*–1) ≥ 0 (7)
Неравенства (6) и (7) в окончательном виде:
 (8)
(8)
Аналогично будем решать неравенство (3). Для этого запишем H(B)
 (9)
(9)
 (10)
(10)
 (11)
(11)
Первое неравенство (3)
H(B) (p*,q*) – H(B) (p*,0) ≥ 0
или с учетом (9) и (10)
 ≥ 0
≥ 0
 (12)
(12)
Второе неравенство (3)
H(B) (p*,q*) – H(B) (p*,1) ≥ 0
Или учитывая (9) и (12)

Неравенства (8) и (12) надо добавить 0≤ p*≤1, 0≤ q*≤1 для решения.
Пример: пусть платежная матрица игрока А 
Платежная матрица игрока B = 
Решение:
1) Найдем величину: C, α, D, β
C = –14, α= –3, D = 9, β = 2
2) Система неравенств (8) и (12) будем записаться в виде:
 (1*)
(1*)
 (2*)
(2*)
Система неравенств (8) и (12) решаем совместно, иначе говоря, нужно найти p* и q*, при которых выполняются все 4 неравенства. В качестве алгоритма используем следующий подход: будем проверять крайние значения 0 и 1, и промежуточные
- если p*=1, то (1b)↔ –14× q* + 3 ≥ 0 ↔ 0≤ q*≤ 
Проверим случай q*= 0, p*=1, то есть выполнение неравенств (2). Легко увидеть, что (2*) не выполняется.
q*= 0, p*=1 не подходит.
- p*=1, 0≤ q*≤  неравенство (2*) не выполняется → не подходит.
неравенство (2*) не выполняется → не подходит.
- q*=0. Тогда (1*) выполняется. А неравенство (1*)↔–14× q* – 3 ≥ 0 ↔ q* ≥ 
Заметим, что при этих q* и p* неравенство (2*) не выполняется. следовательно, 0≤ p*≤1. С учетом этого решим неравенство (1*)
 →q*=
→q*= 
Для нахождения p* поставляем q* =  в (2*) и получаем:
в (2*) и получаем:
 p*=
p*= 
Таким образом, нашли решения.
Вывод: p*=  , q*=
, q*= 
Вычисляем средний выигрыш:

H(A) = –14 ×  ×
×  +3×
+3×  + 2 ×
+ 2 ×  – 1=
– 1= 

H(B) = 9×  ×
×  – 2 ×
– 2 ×  – 3 ×
– 3 ×  + 1 =
+ 1 = 
Кооперативные игры.
Введение. Игра называется кооперативные, если в ней игрокам разрешено обсуждать свои стратегии и договор о совместных действиях игры образуют коалицию.
Теория кооперативных игр изучает тип коалиции который образуется в процессе игры.
Обозначим через N множество всех 4 игроков, игроков нумерации.
N=1,2,3…n. Коалиция показывает любое множество SCN
S- по S множеств N.
число коалиций составлений из R игроков= Ckn
n=  =
= 
Число всевозможной коалиций:
 kn=2n
kn=2n
создание коалицию S множество игроков коалиции действует как один игрок против остальных игроков. Выигрыш коалиций S сумма выигрыша всех игроков этой коалиции.
Опр. Сводится понятие характеристики продукции, показывают функцию которая S  V(S) каждой коалиции S составит соответствие наибольшем выигрыш коалиции.
V(S) каждой коалиции S составит соответствие наибольшем выигрыш коалиции.
Опр. Характерная функция является удовлетворенным неравенством:
Если неравенство Аи В не пересекаются, (А  В
В  )
)
V(A  B)
B) 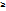 V(A)+V(B) (1)
V(A)+V(B) (1)
Неравенство (1) означает, что в результате образование новой коалиции, выигрыш может только увеличиваться. Требование (1)является логичным, так как создание коалиций было бы бессмысленным, если бы величина выигрыша уменьшается с увеличением числа игр коалиций.
Характеристика функций называется просто если она принимает 2 значения (0 и 1). При этом если V(S)=1, то коалиция S называется выигрыш. Если же V(S)=0, то коалиция S проигрыши.
При создании теории ввели ряд допущений:
1)симметрия
2)режим не зависит от много точных линейных преобразований.
3) режим не должен изменится, если исключить возможные выборы, которые не используют.
4) оптимальность по Парето.
Опр. Характеристическая функция называется адетивной, если
V(A  B)= V(A)+V(B) (2)
B)= V(A)+V(B) (2)
 A1B
A1B  N
N
A  B=
B= 
Если равенство (2) выполняется для любых A  B=
B=  , двух не пересекающих множеств.
, двух не пересекающих множеств.
Теорема:
Характеристическая функция является аддитивной когда и только тогда, когда выполняется равенство.
 (3), где
(3), где
V(i)- выигрыш игрока с номером i
V(N)-выигрыш коалиции, соответствующей из все N игроков.
Доказательство:
чтобы получить формулу (3)нужно показ умножить на имеющей на пересечение и принять формулу (2).
Возьмем две не переменные множители
S и L не пересекаются
S  L=
L=  , тогда
, тогда
V (S)+V(L)  V(S
V(S  L)
L)
 V(S) (1`)
V(S) (1`)
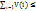 V(L)(2`)
V(L)(2`)
 (3`)
(3`)
Отсутствие А \В – разность 2 множителей, которые состоят их элементов принадлежит множеству А и не принадлежит множителю В.
V(S  L)+V (N \S
L)+V (N \S  L)
L)  V(N)
V(N)
V(N)= 
Если сложить неравенство (1`)+(2`)+(3`), то в левой части получится
V(N)=  )
)  V(S)+ V(L)+V(N\S
V(S)+ V(L)+V(N\S  L)
L)  V(N) (4`)
V(N) (4`)
Все неравенства должны быть равенствами.
Теорема доказана.
Опр. если характер функции является аддитивной, т.е выполняется равенство.
 =V(N)
=V(N)
Тогда кооперативная игра называется не существенной.
Опр. Кооперативная игра называет существенная, если выполняется неравенство.
 V(N)
V(N)
Игра существенная если выигрыш вне коалиции.
S дележи в кооперативных играх. Одна из основных задач кооперативной игры как поднять выигрыши. Если в результате распределения выигрыш коалиции.
Опр. Дележом называется вектор X= (x1, x2,… xn)
17. Дележи в кооперативных играх. (Андриенко)
Одна из основных задач в кооперативных играх: как поделить выигрыш. Если в результате распределения выигрыш некоторого члена коалиции окажется меньше того выигрыша, который он получил бы действуя самостоятельно, то он не захочет входить в коалицию. Отсюда вводится определение:
Дележом называется вектор, который состоит из n- компонентов. X=(x1,х2…хn), вектор которой удовлетворяет условия:
 - (1*)
- (1*)
 - (2*)
- (2*)
(1*)условие индивидуальной рациональности
(2*) условие коллективной рациональности
Объединяться выгодно только в том случае, если каждый игрок, входящий в коалицию получит не меньший выигрыш (1*)
Игроки должны поделить весь выигрыш. Таким образом, делёж – это вектор, удовлетворяющий индивидуальной и коллективной рациональности.
Система, состоящая из множества игроков N, ХФ≠V и множества дележей, удовлетворяющих коллективно-рациональностный, называется классической кооперативной игрой.
Вектор X=(x1,х2…хn) является дележом в кооперативной игре тогда и только тогда, когда выполняются условия:
 (1)
(1)
 (2)
(2)
 (3)
(3)
Доказательство: Если выполняются условия 1-3, то легко проверяется 2 условие из определения дележа. Обратно, если вектор Х является дележом, то достаточно положить  , тогда условия 1 и 3 будут выполнены.
, тогда условия 1 и 3 будут выполнены.
Формула характеристической функции:

V(S)- старая, заданная характеристическая функция
V’(S)- новая, которую требуется построить характеристическая функция
S- коалиция

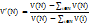
18. Доминирование дележей. (Коморов)
19. Решение Неймона – Моргенштерна. (Маркова)
Если никакие два дележа внутри множества M не доминирует друг друга, а любой дележ вне множества M доминирует дележ их множества М
1)  х,у
х,у  выполенно х не доминирует у и уне доминирует х
выполенно х не доминирует у и уне доминирует х
2) для любого 
 ,
, 
Теорема
НМ – решение содержит С- ядро
Доказательство:
Предложим противное тогда найдется дележ принадлежащий ядру, но не принадлежит НМ
х не принадлежит НМ
в определении НМ найдётся дележ У, который доминирует дележ Х. Но это противоречит определения С-ядро.
Теорема доказана.
Как проверить, что С – ядро не пусто?
Теорема:
Пусть задана игра в 0-1 редуцированной форме, тогда если выполняется неравенство.
V(S)  /n-|S|+1,
/n-|S|+1,
где n – число всех участников игры.
|S|- число участников коалиции.
Причем это неравенство выполняется для всех коалиций, тогда С-ядро коалиции не пусто.
20. 0-1 редуцированная форма кооперативной игры. (Назарова)
Кооперативная игра (IV,V) игра если в0-1, редуцированной форме, если V(i)=0; i=1,2,…,n; V(N)=1
Выигрыш отдельного игрока, если он играет один -0, а если коалицией то 1.
Теорема.
Каждая существенная игра эквивалентна одной и только одой игре в0-1 редуцированной форме.
Доказательство.
Дана игра (IV,V) будем искать игру эквивалентную данной (IV/V”) ~(IV,V), которая к тому же является в игре 0-1 редуцированной форме. Составим уравнение:
V´(i)= KV(i) + Ci=0 i=1,2,…,n
условие эквивалентности
V´(N)=KV(N)+  =1 (n+1)
=1 (n+1)
Всего записано n+1 уравнение
Сложим первые n уравнения

Полученное равенство вычтем из уравнения n+1. Получим:

Кооперативная игра существенная, то []>0 (непонятное слово) обе части можно поделить на эту скобку

Зная K найдем неизвестные Ci= - KV(i)=> 
Найдем характеристическую функцию

Для следующей игры найти эквивалентную, которая представлена в 0-1 редуцированной форме. Найти: V’
V(S)-стадия задания характеристическая форма
V’(S)- новая, требуется построить
S-коалиция
Исходные данные:
V(1)=100 V(1,2)=300 V(1,2,3)= 550
V(2)=150 V(1,3)=350
V(3)=300 V(2,3)=420

 V’ (1) = V’ (2) = V’ (3) =0
V’ (1) = V’ (2) = V’ (3) =0
 V’(1,2,3)=1
V’(1,2,3)=1



21. Вектор – Шепле. (Рыбников)
22. Позиционные игры. (Родченко, Зотова)
Введение
В теории игр используется такое понятие как граф. Граф называется совокупность точек, называющихся вершинами, и соединяющих их линией (ребрами)
Ребра, имеющие одинаковые кольцевые решения называются параллельными.
Ребро, кольцевая решения, которых совпадают, называются петлей.
Если вершина является кольцевой точкой для ребра, то вершина и ребро инцидентные друг к другу.
Маршрут – последовательность ребер ведущих от одной вершины к другой.
Если составляющие ребра маршрута различны, то это путь
Цикл – путь, начальная коими вершины которого совпадают.

Ребра(е1,е2,е4) образуют цифру, т.к. начальные и конечные вершины совпадают.
Граф называется связным, если для любых двух его вершин существует путь их соединяющие.
Деревом называется связный граф несодержащий циклов. Позиционные игры изображаются с помощью деревьев.
Общие сведенья.
Позиционные игры – это бескоалиционные игры, в которых принятие решений рассматривается как многошаговый процесс. В позиционных играх в процессе принятия решений игрок проходит последовательность состояний, в которых приходится принимать решения.
В позиционных играх стратегию можно рассматривать как функции ставящие в соответствии информационному состоянию игрока выбор возможной альтернативы.
Переходы из одного информационного состояния в другое сопровождается получением или утратой информации игроком.
В информационных играх число игроков может быть больше двух.
Пример: 3 игрока выбирают 1 из 4 кандидатов в претенденты.
Правила выбора следующие: начиная с 1 каждый игрок налагает вето на выбор кандидатов единственно оставшийся кандидат считается избранным в результате выбора каждый игрок получает выигрыш:
V1=(5,4,3,7)
V2=(6,7,5,4)
V3=(3,8,5,4)

23. Рис 2.
Дерево содержит одну единственную нормальную вершину (корень дерева)
Корень дерева не идет ни одна ветвь
1) Дерево имеет не менее 1-ой вершины из которой не выходит ни одна ветвь
Эти вершины называются конечными
2) Из корня дерева имеется единственный путь к каждой из остальных вершин дерева.
3) Вершина соответствует определенному состоянию игры перед очередным ходом
Каждую вершину занимает только один игрок.
Вершине присваивается номер равный номеру игрока.
Ходы игроков могут быть личными и случайными.
В описании игры указано какие выборы делает игрок при линейно ходе.
Если ходить случайно, то задается вероятность этих ходов.
Информация игрока задается разбиением вершин на множество.
Рассмотрим решение игры на Рис1 – это игра с полной информацией. Согласно теории игр, такая игра разрешима. И решается эта игра по принципу «доминирования»:
Каждый игрок имеет доминирующие стратегии, которые ему необходимо применять.
Рассмотрим принцип «доминирования» на этом примере.
Из всех вершин предшествующих конечным ходит 3 игрок.
Остальные игроки знают функцию выигрыша 3-го игрока, поэтому они могут предвидеть его решение.С учетом того что шаг 3-го однозначно определен, имеем следующую схему: 
Получили новое дерево, здесь 3-ий игрок по сути не принимает решение.
Финальная вершина определяется ходами игрока 2.
Игрок,1 зная функцию решения 2-го игрока, может предвидеть его ход.
С учетом этого приходим к новому дереву.

В результате если 1-ый игрок отклонит 3-го, то 2-ой игрок вынужден будет отклонить 2-го, а 3-ий 1-го.
Процесс сведения игры к матричной называется нормализацией.
Для нормализации игры нужно перечислить все возможные стратегии игроков и для каждой совокупности стратегий определить выигрыш игроков.

Первый игрок делает свой 1-ый ход выбирая первую или вторую ветвь, затем ход делает 2-ой игрок, у него в каждой вершине имеется два выбора.
Стратегии игроков:
1-ый:
А1- выбирает левую ветвь
А2 – выбирает правую ветвь
2-ой:
В1 – всегда левая ветвь
В2 – всегда правая ветвь
В3 – выбирать ветвь, которую выбрал 1-ый игрок
В4 – выбирать ветвь противоположную той, что выбрал 1-ый игрок
Запишем эту игру в матричной форме:
| В1 | В2 | В3 | В4 | |
| А1 | -2 | -2 | ||
| А2 | -2 | -2 |
Цена игры равна -2
2-ой игрок всегда применяет 4-ую стратегию.
Рассмотрим игру со случайными ходами:
2-ому игроку не сообщают, какой ход выбрал 1-ый игрок.
В этом случае у 2-го игрока только 2 стратегии (В1 и В2)
| В1 | В2 | |
| А1 | -2 | |
| А2 | -2 |
24. Нормализация позиционной игры. (Шумак)
Процесс позиционной игры к матричной – это нормализация.
Нужно перечислить все возможные стратегии игры и для каждой совокупности стратегии определить выигрыш игроков.
1 игрок делает ход выбирая правую или левую ветвь, затем ход делает второй игрок у него в каждой вершине есть 2 выбора:
А1 левая ветви,
А2 правая ветви., Б1 –левая ветви,
Б2правая,
Б3 выбрал ветви первый игрок,
Б2 выбрал противоположный который выбрал первый.
Матричная форма

Нижняя часть игры равно верхней части игры – это оптимальная стратегия.
Рассмотрим игру со случайными ходами, предположим, что второму игру не сообщается выбор первому игроку.




Найти p – игрока









V=-2
V= 
Выигрыш второго игрока уменьшится с 2 до  . Вследствие чего уменьшился выигрыш второго игрока из-за того что ему не сообщают о ходе первого игрока.
. Вследствие чего уменьшился выигрыш второго игрока из-за того что ему не сообщают о ходе первого игрока.






