Сходимость ЛММ. Теорема Далквиста о сходимости
Введем определение сходимости для линейного многошагового метода(ЛММ)
Определение. ЛММ является сходящимся тогда и только тогда, когда для всех задач с начальными условиями(Н.У.) вида 1.2,удовлетворяющих условиям теоремы 1.1. на интервале [0;T] и для всех начальных точек 
,которые удовлетворяют условию 1.6.1,решение 
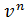удовлетворяет
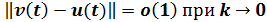
(1.6.2)
равномерно для всех t из [0;T]
Теорема 1.1 Пусть f(u,t) будет непрерывна по t и равномерно непрерывно по u для всех t из [0,T](т.е. выполняются условия Липшица по u).Тогда существует единственная дифференцируемая функция u(t),которая удовлетворяет задаче с н.у. 1.2.
Условие 1.6.1. Значения в начальных точках удовлетворят условию согласованности т.е
для n, s <=n<=s-1
Задача 1.2 Задана функция f, T>0, 
, требуется определить дифференцируемую функцию u(t) определенную для всех t из отрезка [0,T] такую что
a) u(0)=u0
b) ut(t)=f(u(t),t) для всех t из отрезка [0,T]
Сходящийся ЛММ обеспечивает получение точного значений u при k->0,для любого t из [0,T]
Замечания по поводу определения сходимости ЛММ
1) Условие 1.6.2 о пределе при k->0 для каждого фиксированного t.Т.к. v(t) задается на дискретной сетке, это значит что k неявно ограничивается значениями t/n.Данное ограничение можно ослабить потребовав,чтобы 
2) Сходящаяся ЛММ должна работать для всех корректно поставленных задач с н.у.
Формула, которая работает только для ограниченного класса начальных задач например только с достаточно гладкими коэффициентами, будет чувствительным к возмущениям
3) 
относится к точному решению ЛММ; ошибки округления не учитываются в определении сходимости. Однако, данные упрощения обоснованны,т.к. ошибки дискретизации и ошибки в начальных точках учтены, с помощью 1.6.1, условия согласованности регулируют источники ошибок почти одинаково.
4)Заметим, что условие 1.6.1 достаточно слабое, требующей точность в начальных точках только o(1) или O(k). В отличие от точности O(k^2) которая требуется на последующих шагах метода в соответствии с определением согласованности. Причина такого различия достаточно проста: ошибки в начальных шагах присутствуют только в s шагах, в то время как последующие ошибки представлены θ(k^-1) раз. В уравнениях в частных производных в граничных условиях точность граничных условий также может быть на 1 порядок меньше
Теорема Далквиста. ЛММ сходится ó ЛММ согласован и устойчив
Кроме сходимости,полезно было знать точность решения полученного с помощью ЛММ. Для того чтобы гарантировать точность p порядка условия 1.6.1
могут быть усилены
(1.6.4)
Следующая теорема подтверждает, что для устойчивой ЛММ с гладкими (smooth) коэффициентами примененная к начальной задаче 1.2, локальные ошибки складываются, как и ожидалось
Теорема. Пусть задача с н.у. вида 1.2,которая удовлетворяет условиям теоремы 1.1. на интервале [0,T], дополнительно положим, что f(u,t) p раз непрерывно дифференцируема по u и t.Пусть решение вычисляется сходящимся ЛММ с порядком точности >=p c значениями в начальных точках удовлетворяющих 1.6.4.. Тогда решение удовлетворяет
(1.6.5)
Равномерно для всех t из [0,T]
