Содержание
Введение 3
1 Теоретическая часть 4
2 Расчет процесса затвердевания отливки 13
2.1 Определение времени полного затвердевания отливок в песчано-глинистой форме по методике Н. Г. Гиршовича и Ю. А. Нехендзи 13
2.2 Определение закона затвердевания отливок - t=f(e) по методике Н. И. Хворинова, А. И. Вейника, Г. Ф. Баландина 16
2.3 Построение графиков зависимости e=f(t) для плиты, цилиндра и шара по полученным данным с использованием программных средств Microsoft Excel 21
2.4Построение температурных полей в затвердевшей корочке отливки в моменты затвердевания корочки толщиной 0,5 R, полного затвердевания отливки 26
Заключение 30
Список использованных источников 31
Приложение 32
Введение
Целью курсовой работу по курсу «Моделирование процессов и объектов в металлургии» является закрепление знаний, полученных студентами при изучении теоретического курса и использование их для решения практических задач, связанных с тепловой теорией затвердевания отливки. Студент должен уметь определять время и коэффициент затвердевания отливок в форме, используя для расчетов ПЭВМ с имеющимся программным обеспечением.
Так как расплав, затвердевающий в литейной форме, представляет собой сложную систему, то построение математических моделей процессов затвердевания отливок связано с трудностями практического и теоретического характера. При строгом аналитическом решении необходимо учитывать большое число различных факторов: основных особенностей реальной технологии изготовления отливки, конфигурации отливки, свойств материала отливки и формы, особенностей кристаллизации сплавов в интервале температур и др. Создание общей теории такой сложной системы, охватывающей все стороны процессов затвердевания, - задача, невыполнимая из-за недостатка знаний о явлениях, составляющих процесс затвердевания, и из-за чрезвычайных и практически непреодолимых математических трудностей. На основе экспериментальных данных и наблюдений необходимо выявить те важнейшие факторы, которые определяют ход процесса в целом или его стадий. Далее необходимо упростить задачу, отбросив менее важные факторы, чтобы для всего процесса или его частей построить более простую математическую модель, которая учитывает лишь выявленные важнейшие факторы.
Важнейшим фактором, обуславливающим протекание процесса затвердевания является теплообмен между затвердевающим расплавом и литейной формой. Тепловая теория затвердевания отливок основана на использовании математических моделей теории теплообмена.
Теоретическая часть
Под кристаллизацией в широком смысле в теории литейных процессов понимается процесс формирования структуры отливок при переходе металла из жидкого состояния в твердое. Процесс превращения сплавов из жидкого состояния в твердое является теплотехническим, поскольку он обязательно сопровождается теплоотводом скрытой и физической теплоты. Но одновременно процесс превращения является физико-химическим, поскольку он сопровождается образованием конгломерата кристаллов. Первый процесс может быть назван затвердеванием, второй – кристаллизацией.
Первые работы по затвердеванию основывались на известных решениях Ляме и Клапейрона или Д. Стефана задачи о замерзании воды или промерзании влажного грунта. Ляме и Клапейрон и Стефан рассматривали воду и влажный грунт как полуограниченное (полубесконечное) тело, на поверхности которого поддерживается постоянная температура. Формулу, полученную ими, называют «законом квадратного корня» затвердевания отливки:
, (1)
где ε – толщина затвердевшей корочки, м;
k – постоянная величина, получившая применительно к литейным процессам название константы затвердевания, м/с0,5;
t - время, с.
На рисунке 1 дана схема распределения температуры затвердевающей отливки, где TЗ – температура заливки сплава, К; ТКР – температура кристаллизации сплава (для сплавов, кристаллизующихся в интервале температур – температура ликвидус), К; Tк – температура контакта отливка-форма, К; 
– средняя температура затвердевшей корочки металла, К; 
– средняя температура прогретого слоя формы, К; 
– начальная температура формы, К; у – координата, отсчитываемая от фронта затвердевания в направлении к поверхности отливки, м; х – координата, отсчитываемая от поверхности отливки в направлении к фронту затвердевания, м; z – координата, отсчитываемая от поверхности отливки в форму, м (индекс ф означает принадлежность характеристики к форме, м – принадлежность к металлу отливки).
Рисунок 1 – Схема распределения температуры в форме и затвердевающей
отливке
где bф, bм–коэффициент аккумуляции тепла формы и металла, Вт.с0,5/(м2.К),
В постановке задачи Шварца (затвердевание полуограниченного слитка, в результате охлаждения его в полуограниченной изложнице) Tк отливка-форма остается постоянной в процессе всего периода кристаллизации, следовательно к задаче можно применить квазистационарный подход.
Температура контакта Tк отливка-форма определяется по формуле, предложенной Н. И. Хвориновым:
, (2)
; 
, (3)
где с, 
, 
- теплоемкость, плотность и теплопроводность металла и формовочной смеси соответственно.
Величина k представляет собой корень следующего весьма сложного трансцендентного уравнения и зависит от множества факторов, характеризующих процесс затвердевания (теплофизических коэффициентов материалов, температуры и т. д.). Трудность определения величины k из трансцендентного уравнения заставила исследователей в области литейного производства находить ее опытным путем.
Долгое время формула (1) служила основным расчетным выражением, с помощью которого определялась толщина затвердевшей корочки. Эту формулу начали применять для расчета отливок различной конфигурации, охлаждающихся в самых разнообразных условиях. Конкретные условия затвердевания пытались учитывать, выделяя частные связи, существующие между величиной k и отдельными параметрами процесса. Например, находили связь между величиной k и перегревом заливаемого металла, свойствами формы и т. д.
Однако анализ показывает, что фактические условия затвердевания отливки в форме коренным образом отличаются от тех условий, которые рассматривались Ляме, Клапейроном и Стефаном. Действительно, реальная отливка представляет собой тело конечных размеров. Фронт затвердевания только в отдельных частных случаях является плоским, в большинстве же случаев практики приходится иметь дело с отливкой сложной конфигурации. Интенсивность теплообмена на поверхности отливки может колебаться от бесконечно малых до бесконечно больших значений. В результате температура поверхности отливки почти никогда не остается постоянной (характер изменения температуры поверхности зависит от интенсивности теплообмена и конфигурации отливки); интенсивность теплообмена, в свою очередь, определяется свойствами зазора, находящегося между отливкой и формой. Кроме того, распределение температуры в перегретом металле вследствие конвекции никогда не соответствует тому распределению температуры, которое имеет место в талом грунте.
Большое экспериментальное и теоретическое исследование процесса затвердевания отливки в неметаллической форме выполнил Н. И. Хворинов (1939 – 1940 гг.). На основе анализа количества теплоты, поступающей из отливки в форму, Н. И. Хворинов пришел к формуле, которая позволяет определять зависимость толщины ε затвердевшей корки от времени τ с учетом перегрева металла над температурой кристаллизации:
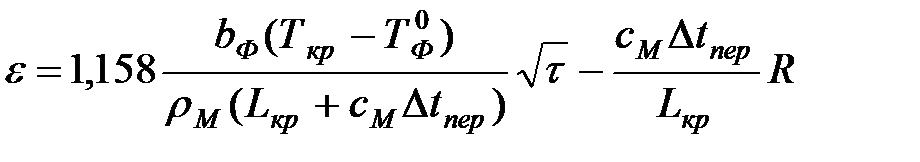, (4)
где Lкр – удельная теплота кристаллизации металла отливки, Дж/кг;
Δtпе р– перегрев металла над температурой кристаллизации, 0С;
Δtпер = Тз - tкр; см– удельная теплоемкость металла отливки, Дж/(кг0С);
rм, rф – плотность металла отливки и материала формы, кг/м3;
R – так называемый приведенный размер отливки, равный отношению объема отливки Vо к площади F0 поверхности охлаждения (R=V0/F0).
Н. И. Хворинов в своих работах впервые широко использовал понятие приведенного размера отливки, имеющее большое значение при анализе процесса затвердевания металла в неметаллической форме.
Отсутствие общего решения задачи о затвердевании металла в литейной форме, из которого вытекали бы различные частные решения, отвечающие конкретным условиям литья, послужило толчком к принятию исследователями следующего решения. В каждом конкретном случае находятся строго обоснованные упрощения задачи, выводятся расчетные формулы, которые позволяют вычислить параметры процесса затвердевания отливки в зависимости от свойств формы, заливаемого металла и др.
Н. Г. Гиршовича и Ю. А. Нехендзи решали задачу о затвердевании отливки в металлической и неметаллической формах. Авторы предлагают не искать частные решения задачи для отдельных видов литья, а воспользоваться наиболее простым решением для какого-либо конкретного случая и затем вводить в это решение поправки, обусловленные влиянием реальных усложняющих факторов. Следует отметить, что основная идея авторов, направленная на отыскание универсального решения, которое было бы справедливо для любых условий затвердевания отливки, является весьма ценной. Однако надо иметь в виду, что достаточно точное универсальное решение при современном состоянии теоретических знаний получить невозможно.
Н.Г. Гиршович и Ю.А. Нехендзи разработали наиболее общую методику расчета процесса затвердевания отливок на основе универсальной формулы для определения времени полного затвердевания:
, (5)
где R – приведенная толщина отливки, м;
μконф, μпер, μинт, μзаз – поправочные коэффициенты на конфигурацию, на перегрев металла, на интервал кристаллизации, на зазор, образованный газовой прослойкой и краской.
Для неметаллической формы можно записать:
, (6)
Поправочные коэффициенты определяются аналитически или таблично.
Поправка на конфигурацию для случая затвердевания отливки в неметаллической форме для отливок типа, плита, цилиндр и шар принимается μконф =1.
Поправка на перегрев металла над температурой кристаллизации, вызывающий прогрев формы до начала затвердевания и соответствующее уменьшение интенсивности теплоотвода в период кристаллизации, определяется по формуле
, (7)
где b - коэффициент, равный: для плиты 1,75; для цилиндра 1,25; для шара 1,1.
Поправочный коэффициент μинт рассчитывают по формуле
, (8)
Для неметаллической формы влиянием газового зазора можно пренебречь, принимая μзаз=1.
В 1950—1952 гг. Вейником А.И. решалась задача о затвердевании отливки в различных формах. Автор исследовал интенсивность теплообмена между отливкой и формой и расчленил весь процесс охлаждения отливки на четыре характерные стадии, соответствующие заполнению формы (течение металла), отводу теплоты перегрева от неподвижного металла, затвердеванию металла и охлаждению полностью затвердевшей отливки. На этой основе были получены упрощенные решения для случаев затвердевания металла в неметаллической форме, окрашенном кокиле и изложнице, учитывающие все главные особенности процесса. Первоначально при решении задачи автор приближенно принимал линейный закон распределения температуры в сечении отливки (нелинейность реальных температурных кривых учитывалась особыми поправками). Затем в качестве температурной кривой была принята парабола n-го порядка. Это позволило преобразовать дифференциальное уравнение теплопроводности в частных производных в алгебраическое и получить удовлетворительные по точности результаты как для закона продвижения фронта затвердевания, так и для температурного поля отливки.
Закон распределения температуры в затвердевшей корочке металла (рисунок 1) задается, по А. И. Вейнику в виде параболы n-го порядка
, (9)
где Тм – температура металла в точке с координатой х, К;
n – величина, определяемая из опыта, ее значения приведены в таблице 1.
Таблица 1 – Зависимость величины показателя n от конфигурации отливки
| Отливка | n |
| плита | |
| цилиндр | 0,75 |
| шар | 0,59 |
А. И. Вейник получил следующие безразмерные уравнения для определения положения границы затвердевания во времени:
для плоской отливки
, (10)
для цилиндрической отливки, затвердевающей снаружи
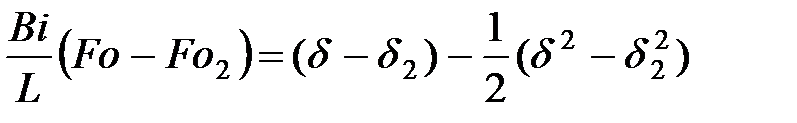, (11)
для шаровой отливки, затвердевающей снаружи
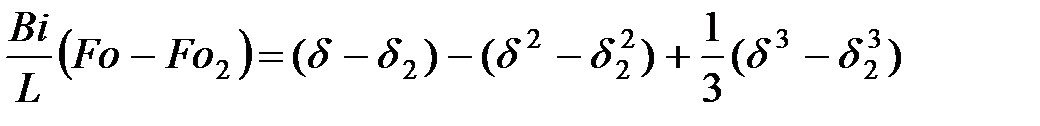, (12)
где Fo – критерий Фурье (безразмерное время) для текущего времени t;
Fo – критерий Фурье для времени, прошедшего с момента заливки до момента снятия перегрева;
Bi - критерий Био;
d, d2 - относительная толщина затвердевшей корочки металла к моменту t и t2 соответственно.
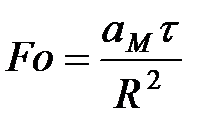, (13)
, (14)
где аМ – теплопроводность металла отливки, 
;
- коэффициент теплоотдачи, Вт/(м2К);
L – критерий теплоты кристаллизации.
. (15)
Г. Ф. Баландин предложил следующую методику определения закона затвердевания отливок в песчаной форме:
, (16)
где l0 - характерный размер отливки: для плиты это половина толщины, для цилиндра и шара – радиус, м;
rтв.м – плотность метала отливки в твердом состоянии, кг/м3;
n – коэффициент, зависящий от конфигурации отливки: для плоской отливки n=0, для цилиндрической n=1, для шаровой n=2; t - время, при котором затвердела корочка толщиной e, с;
t1 – время полного охлаждения перегретого расплава, с.
Время полного охлаждения перегретого расплава в песчаной форме (с учетом мгновенного заполнения формы расплавом) можно определить по формуле
, (17)
где сж.м, rж.м - удельная теплоемкость и плотность жидкого расплава, Дж/(кг0С), кг/м3.
2 Расчет процесса затвердевания отливки
В таблице 2 приведены данные для расчета процесса затвердевания отливки.
Таблица 2 – Исходные данные для расчета
| № варианта | Материал отливки | Размеры отливки, мм | 
| 
| ||
| плита | цилиндр | шар | ||||
| Оловянная бронза | 30х200х200 | Ø 30х200 | Ø 30 |
2.1 Определение времени полного затвердевания отливок в песчано-глинистой форме по методике Н. Г. Гиршовича и Ю. А. Нехендзи.
2.1.1 Определим температуру заливки металла. По таблице А.1 приложения А для оловянной бронзы:
Значит 
2.1.2 Необходимые для расчетов данные о теплофизических свойствах металла отливки и материала формы (теплота кристаллизации, плотность и теплоемкость чугуна, и коэффициент аккумуляции тепла формы) выберем из таблиц А.1, А.2 приложения А:
2.1.3 Определим коэффициент затвердевания отливки по следующей формуле:
2.1.4 Определим поправочные коэффициенты, приведенный размер и время
полного затвердевания плоской отливки:
Поправочные коэффициенты:
для плиты β=1,75;
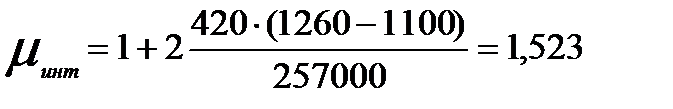
Приведенный размер отливки:
V=0.03*0.2*0.2=0.0012 м3
F0=2(0.03*0.2+0.2*0.2+0.03*0.2)=0.104 м3
R=0.0012/0.104=0.0115м;
Время полного затвердевания отливки:
2.1.5 Определим поправочные коэффициенты, приведенный размер и время
полного затвердевания цилиндрической отливки:
Поправочные коэффициенты:
для цилиндра β = 1,25;
Приведенный размер отливки:
V= 
r2l=3.14*0.0152*0.2=0.0001413 м2
F0=2 
R2+2 
Rh=2*3.14*0.0152+2*3.14*0.015*0.2=0.0203м2 R=0.0001413/0.0203=0.00696м
Время полного затвердевания отливки:
2.1.6 Определим поправочные коэффициенты, приведенный размер и время
полного затвердевания шаровой отливки:
Поправочные коэффициенты:
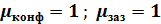
для шара β = 1,1;
Приведенный размер отливки:
V= 
R3= 
*3.14*0.0153= 0,0000141 м3
F0=4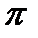 
R2=4*3.14*0.0152=0.00283 м2
R=0,0000141 /0.00283=0.00498 м
Время полного затвердевания отливки:
2.2 Определение закона затвердевания отливок - t = f(e) по методике Н. И. Хворинова, А. И. Вейника, Г. Ф. Баландина
2.2.1 Для определения закона затвердевания по методике Н. И. Хворинова необходимо преобразовать уравнения 4,10,11,12,16 к виду t=f(e).
Формула 4 после преобразования будет иметь вид:
Изменяя толщину нарастающей корочки e от 0 до R, с шагом по координате х 0,0001 м, определим время затвердевания корочки толщиной e.
Для плоской отливки при e = 0
полное время затвердевания при e = R
Для цилиндрической отливки при e = 0
полное время затвердевания при e = R
Для шаровой отливки при e = 0
полное время затвердевания при e = R
2.2.2 Определим закон затвердевания отливок по методике А.И.Вейника.
Для плоской отливки:
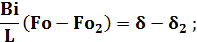
При e = 0: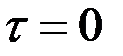 
с.
При e = R: 
Для цилиндрической отливки:
При e = 0: 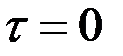с.
При 
Для шаровой отливки:
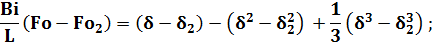
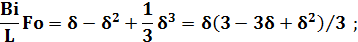
При e = 0: 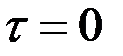с.
При e = R: 
2.2.3 Определим закон затвердевания отливок по методике Г.Ф.Баландина:
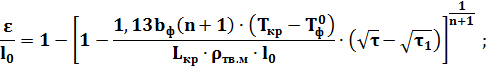
Для плоской отливки n=0:
R =0,0115;
При e = 0: 
При e = R:
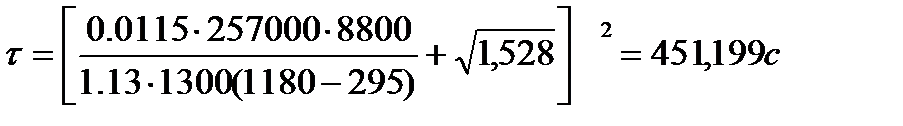
Для цилиндрической отливки n=1:
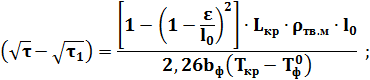
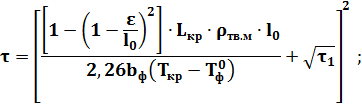
l0=0,015 м;
R=0, 00696 м;
При e = 0: 
При e = R:
Для шаровой отливки n=2:
l0=0, 015 м;
R=0, 00498 м;
При e = 0: 
При e = R:
2.3 Построение графиков зависимости e=f(t) для плиты, цилиндра и шара по полученным данным с использованием программных средств Microsoft Excel
Графики зависимости толщины затвердевания корочки от времени затвердевания отливки по методике Н.И.Хворинова представлен на рисунках 2, 3, 4.
Рисунок 2 – Зависимость толщины затвердевшей корочки от времени затвердевания
по методике Н.И.Хворинова (для плиты)
Рисунок 3 – Зависимость толщины затвердевшей корочки от времени затвердевания
по методике Н.И.Хворинова (для цилиндра)
Рисунок 4 – Зависимость толщины затвердевшей корочки от времени затвердевания
по методике Н.И.Хворинова (для шара)
Графики зависимости толщины затвердевания корочки от времени затвердевания отливки по методике А.И.Вейника представлен на рисунках 5, 6, 7.
Рисунок 5 – Зависимость толщины затвердевшей корочки от времени затвердевания
по методике А.И.Вейника (для плиты)
Рисунок 6 – Зависимость толщины затвердевшей корочки от времени затвердевания
по методике А.И.Вейника (для цилиндра)
Рисунок 7 – Зависимость толщины затвердевшей корочки от времени затвердевания
по методике А.И.Вейника (для шара)
Графики зависимости толщины затвердевания корочки от времени затвердевания отливки по методике Г.Ф.Баландина представлен на рисунках 8, 9, 10.
Рисунок 8 – Зависимость толщины затвердевшей корочки от времени затвердевания
по методике Г.Ф.Баландина (для плиты)
Рисунок 9 – Зависимость толщины затвердевшей корочки от времени затвердевания
по методике Г.Ф.Баландина (для цилиндра)
3 bnJldi54bWxQSwECLQAUAAYACAAAACEAllUfAAABAAAqAgAADgAAAAAAAAAAAAAAAABYAwAAZHJz L2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAqxbNRrkAAAAiAQAAGQAAAAAAAAAAAAAAAACEBAAA ZHJzL19yZWxzL2Uyb0RvYy54bWwucmVsc1BLAQItABQABgAIAAAAIQDng9B98gAAAFABAAAgAAAA AAAAAAAAAAAAAHQFAABkcnMvY2hhcnRzL19yZWxzL2NoYXJ0MS54bWwucmVsc1BLAQItABQABgAI AAAAIQCLyooP2AkAANQgAAAVAAAAAAAAAAAAAAAAAKQGAABkcnMvY2hhcnRzL2NoYXJ0MS54bWxQ SwUGAAAAAAcABwDLAQAArxAAAAAA "> 
Рисунок 10 – Зависимость толщины затвердевшей корочки от времени затвердевания по методике Г.Ф.Баландина (для шара)
Построение температурных полей в затвердевшей корочке отливки по формуле (9) в моменты затвердевания корочки толщиной 0,5R, полного затвердевания отливки
Определим температуру контакта отливка-форма:
Рисунок 11 – Температурное поле в затвердевшей корочке толщиной 0,5R
(для плиты)
Рисунок 12 – Температурное поле в затвердевшей корочке толщиной 0,5R
(для цилиндра)
Рисунок 13 – Температурное поле в затвердевшей корочке толщиной 0,5R
(для шара)
Рисунок 14 – Температурное поле в затвердевшей корочке толщиной R
(для плиты)
Рисунок 15 – Температурное поле в затвердевшей корочке толщиной R
(для цилиндра)
Рисунок 16 – Температурное поле в затвердевшей корочке толщиной R
(для шара)
Заключение
В ходе данной работы были закреплены знания, полученные при изучении теоретического курса. Эти знания были использованы для решения практических задач, связанных с тепловой теорией затвердевания отливки.
По полученным данным с использованием программных средств Microsoft Excel были построены графики, отражающие зависимость толщины затвердевшей корочки от времени.
Также были построены температурные поля в затвердевшей корочке отливки в моменты затвердевания корочки толщиной 0,5R, и в момент полного затвердевания.
Таблица 3 – Обобщение методик расчета времени полного затвердевания отливки
| Методика расчета | Время полного затвердевания отливок, с | ||
| плита | цилиндр | шар | |
| Н.Г.Гиршович и Ю.А.Нехендзи | 688,265 | 243,841 | 123,58 |
| Н.И.Хворинов | 506,728 | 185,610 | 95,020 |
| А.И.Вейник | 355,86 | 107,68 | 51,37 |
| Г.Ф.Баландин | 451,199 | 100,926 | 44,089 |
Список использованных источников
1. Баландин Г. Ф. Основы теории формирования отливки. Ч. 1. Тепловые основы теории литья. Затвердевание и охлаждение отливки: Учеб. пособие / Г. Ф. Баландин – М.: Машиностроение, 1976 г. – 328 с.
2. Вейник А. И. Теория затвердевания отливки / Вейник А. И. – М.: Машгиз, 1960. – 436 с
3. Вейник А.И. Расчет отливки / А.И. Вейник – М.: Машиностроение. – 1964. – 402 с.
4. Методическое указание. Расчет процесса затвердевания отливок.
Приложение А
Таблица А. 1 – Теплофизические свойства некоторых металлов и литейных сплавов
| Материал | Тл, К | Тс, К | LКР, 
| см,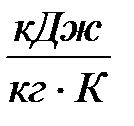 
| rм, 
| lм, 
| bм, 
| ам. 10 5, 
|
| Силумин (13% Si) | 0,42 | 1,43 |
Таблица А. 2 – Теплофизические свойства формовочных смесей
| Материал отливки | lФ,
| сФ,
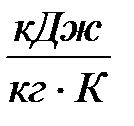
| rФ,
| bФ,
| аф. 10 7,
|
| Алюминиевые сплавы | 0,66 | 1,59 | 2,58 |
Условные обозначения:
Тл – температура ликвидус, К;
Тс – температура солидус, К.
