Методические пособияпо курсу (библиотека ЛЭТИ).
Бондарев А.С., Червинская Н.М.. Линейная алгебра в примерах и задачах: Учебное пособие. - СПбГЭТУ «ЛЭТИ»,2002.
Белопольский А.Л., Бодунов Н.А., Червинская Н.М. Типовые расчеты по курсу „Алгебра и геометрия “: Учебное пособие. СПб.: Изд-во СПбГЭТУ “ЛЭТИ”, 2008.
3. Колбина С.А., Пилюгин С.Ю.. Линейная алгебра: Учебное пособие.- СПбГЭТУ«ЛЭТИ»,2009.
4. Настольный справочник инженера:
Двайт Г.Б. Таблицы интегралов и другие математические формулы. «Наука»
======================================
Самостоятельная работа - «Типовые расчёты» по каждому разделу курса. [Выдача –(2недели)-Отчёт]→Исправления→ ЗАЧЁТ
Отчёт по ТР (предпочтительно в тонкой школьной тетрадке) включает:
1) Титульный лист («ТР по теме …; вариант № …; студент …. гр. …»)
2) Вариант + текст «Задание».
3) Метод (алгоритм) ↑решения задачи: используемые при выполнении работы
определения, свойства, формулы.
4) Выполнение работы(в соответствии с «Заданием»).
5) РЕЗУЛЬТАТЫ ( в соответствии с «Заданием»): численные результаты
представляются в форме: х =√3 или х≈1.732(3 верные значащие цифры мантиссы).
6) « Исправление » незачтенной части Отчёта: Исправление, дата→ выполнение всей
части работы → соответствующий РЕЗУЛЬТАТ → ЗАЧЁТ!
ТР: [Выдача –(2недели) - Отчёт]→ 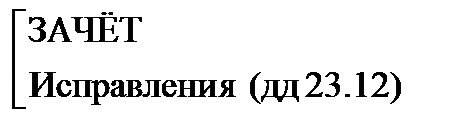 → ЗАЧЁТ (до 30.12)
→ ЗАЧЁТ (до 30.12)
Предисловие - Элементы «математической символики».
Пусть А(х), В(х) – утверждения о «х».
1) Символ “ ⇒ ” «импликация»: A(х) ⇒ B(х) – « из А(х) следует В(х) ≡ если верно А (х), то верно В (х) »
2) Символ “ ó ” «эквивалентность, равносильность»: A(х) ó B(х) – « А(х) и В(х) эквивалентны»: 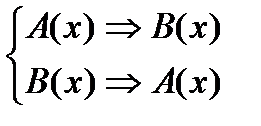
3) Символ “  ” «И, ОДНОВРЕМЕННО»: А (х)
” «И, ОДНОВРЕМЕННО»: А (х)  В (х) - « А(х) И В(х) одновременно» А
В (х) - « А(х) И В(х) одновременно» А  В ó
В ó  ;
;
4) Символ “  ” «дизъюнкция, ИЛИ»: А
” «дизъюнкция, ИЛИ»: А  В - « А ИЛИ В, имеет место хотя бы одно» … А(х)
В - « А ИЛИ В, имеет место хотя бы одно» … А(х)  В(х) ó
В(х) ó 
5) Символ “  ” «для любого»: «
” «для любого»: «  - для всякого (каким бы ни было) «х» верно А(х)»
- для всякого (каким бы ни было) «х» верно А(х)»
6) Символ “  ” «существует, найдётся»:«
” «существует, найдётся»:« - существует(найдется) такое «х»,для которого верно А(х)»
- существует(найдется) такое «х»,для которого верно А(х)»
«∄» «не существует»
7) Символ “ 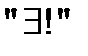 ” «существует единственное»:«
” «существует единственное»:« существует единственное «х» такое, что верно А(х)»
существует единственное «х» такое, что верно А(х)»
Глава I“ МНОЖЕСТВА”.
Символика и операции.
Понятие множества (синонимы- совокупность, система, набор …) является исходным (аксиома-
тическим) понятием.
Запись A={a:F(a)} – множество « A» элементов « a», удовлетворяющих «условию принадлежности F(a) ». Числовые множества могут быть заданы перечислением элементов, формулой, уравнением, неравенством, их системами. Множество может быть пустым (не содержит ни одного элемента), конечным и бесконечным.
Пустое множество обозначают символом  .
.
Пусть A={a:F(a)}. Символы  обозначают принадлежность/непринадлежность элемента множеству: F(b) ⇒ b∊A- «a принадлежит(является элементом ) A»;
обозначают принадлежность/непринадлежность элемента множеству: F(b) ⇒ b∊A- «a принадлежит(является элементом ) A»;  - «b не принадлежит(не является элементом ) множества A». Элементами множества в курсе могут быть числа, векторы, матрицы, функции, множества.
- «b не принадлежит(не является элементом ) множества A». Элементами множества в курсе могут быть числа, векторы, матрицы, функции, множества.
Например,
1) Множество A={1,2,{3,4}} содержит 3 элемента: 
 .
.
2) B={bn=b1∙qn-1; q≠0 ∧ n=1,2,…} – бесконечное множество членов геометрической прогрессии со знаменателем q.
3) X={x: x2+x-2=0)} = {1,-2} – множество решений уравнения.
X={x: x2+1=0} = 
4) С={(a,b): a,b  {0,1,2,3,4,5,6,7,8,9} ∧ a≠0} – множество упорядоченных пар цифр – множество 90 двузначных чисел: NC= 9(способов выбрать а )∙10(b)=90.
{0,1,2,3,4,5,6,7,8,9} ∧ a≠0} – множество упорядоченных пар цифр – множество 90 двузначных чисел: NC= 9(способов выбрать а )∙10(b)=90.
Известно, что для чисел определены отношения равенства «=» и сравнения – строгие «</>» и нестрогие «≤ / ≥» неравенства: 2<3 и 2≤3 (2 не больше 3 или 3 не меньше 2) и
операции сложения «+», вычитания «-» и умножения «х».
Пусть заданы множества A={a}, B={b}, С={c}. Определим для множеств:
1) отношения:
- равенство «=»: A=B ó  - множества состоят из одинаковых элементов.
- множества состоят из одинаковых элементов.
- включения «⊆»: А⊆B ó  « А содержится в В (А является подмножествомВ)
« А содержится в В (А является подмножествомВ)
Следствие. Очевидно, что  . Можно доказать, что конечное множество с n элементами имеет 2nподмножеств.
. Можно доказать, что конечное множество с n элементами имеет 2nподмножеств.
Например, множество A={1,2,{3,4} } имеет 23 =8 подмножеств:
⌀, A, {1}, {2},{{3,4)}, {1,2}, {1,{3,4}}, {2,{3,4}} ⊆ A
2) операции:
- объединение(“сумма”) множеств «⋃»: С=A ⋃ B ó  - состоит только из тех элементов, которые принадлежат хотя бы одному из множеств.
- состоит только из тех элементов, которые принадлежат хотя бы одному из множеств.
- пересечение(“произведение”)множеств «⋂»: С=A ⋂ B ó  - состоит только из тех элементов, которые принадлежат обоим множествам.
- состоит только из тех элементов, которые принадлежат обоим множествам.
- разность множеств «\»: С=A \ B ó  - состоит только из тех элементов A, которые не принадлежат В.
- состоит только из тех элементов A, которые не принадлежат В.
| МНОЖЕСТВO A={a: F(a)} óF(α) ==> α∊A; НЕ F((α)) ==> α∉A |
| A={a}, B={b}, C={c} |
| Включение “⊆”: A⊆B ó∀a∊A: a∊B∧; ∀b∊B: b∊A |
| Объединение множеств “U”: C=A⋃Bó∀c∊C: c∊A ∨ c∊B |
| Пересечение множеств “⋂”: C=A⋂Bó∀c∊C: c∊A ∧ c∊B |
| Разность множеств “\”: C=A\ Bó∀c∊C: c∊A ∧ c∊B |
Иллюстрация «кругами Эйлера»: каждая точка круга – элемент множества.
| C |
| B |
| A |
| B |
| A |
| B |
| A |
| A |
| B |
BÌA || C=AÇB || C=AÈB || C=A/B
 ||
||  ||
||  ||
|| 
3) Множество A={a} называется замкнутым относительно операции (*), если результат операции для любых элементов множества принадлежит множеству

Известно, что числовые множества:
N={1,2.3,…,n,n+1,…} – множество натуральных чисел замкнуто отн. “+” и “x”, HO не “-”.
Z={0,±1, ±2,…., ±n, ±n+1,…} - множество целых чисел замкнуто отн. “+”,“x” и ”-“, HO не “ 
Q =  - множество рациональных чисел замкнуто отн. “+”, ”-“, “x”, “
- множество рациональных чисел замкнуто отн. “+”, ”-“, “x”, “  ”
”
 х- бесконечная периодическая десятичная дробь:.
х- бесконечная периодическая десятичная дробь:.  (3 в.з.ц)
(3 в.з.ц)
Иррациональные числа – числа, определяемые бесконечной непериодической десятичной дробью.
R = Q U {Ирр.} - множество вещественных чисел 
Замечание. Во множестве вещественных (действительных) чисел R:
[1] определены:
- модуль числа “|a| ”: 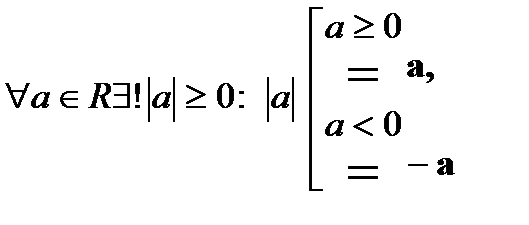 ;
;
- “арифметический корень натуральной степени 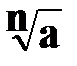 ”.
”.




 ,
, 

ЭКЗ-1 Записать определение |x+3| и найти решения уравнения |x+3|= 2x-5
ЭКЗ-2 Записать определение (х+3)1\2 и найти решения уравнения (х+3)1\2 = 2x-5
[2] В зависимости от дискриминанта D=b2-4∙a∙c квадратноеуравнение ax2+bx+c=0 
 имеет либо одно, либо два решения, либо решений не имеет.
имеет либо одно, либо два решения, либо решений не имеет.

[3] не определены: деление на ноль и корень натуральной степени из отрицательного числа
Вещественное число отображается точкой М(х)с координатой “x” на числовой прямой (ЧП): óM(x).
[5] В R определены подмножества – “ интервалы”:
[a,b] = {x: a≤x≤b} 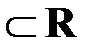 – закрытый; (a,b) = {x: a<x<b} – открытый; [a,b), (a,b] – полуоткрытые
– закрытый; (a,b) = {x: a<x<b} – открытый; [a,b), (a,b] – полуоткрытые
| xóM(x) |
| [a; |
| [a; |
| (a; |
| x |
| b) |
| b) |
| b] |
| Числовая прямая и интервалы в R |






