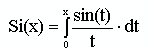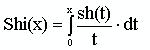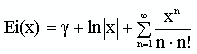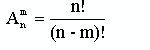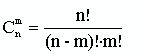6.1. Цель работы
Научиться создавать динамические подключаемые библиотеки (DLL) при помощи Microsoft Visual Studio.
6.2. Теоретические сведения
Операционная система Windows исходно задумывалась как многозадач- ная, что означает возможность выполнения на одном персональном компьюте- ре (ПК) нескольких задач. Часто требуется, чтобы такие задачи взаимодейство- вали между собой, обменивались информацией, причем на основе стандартного
механизма, не требующего от программиста в разрабатываемом им приложе- нии реализации способа такого взаимодействия.
Самый простой способ обмена информацией между программами – это использование динамически подключаемых библиотек *.dll. Библиотека *.dll – это не программа, а хранилище программного кода (например, функций) и ре-сурсов (например, форм). Она подключается к программе динамически, после того как программа запущена. Использовать библиотеки *.dll очень удобно. Пусть, например, имеется программа прогнозирования некоего значения на ос- новании данных, вводимых пользователем. В этом случае будет целесообразно создать пользовательский интерфейс, а сам алгоритм расчета прогноза выде- лить в отдельную функцию и поместить его в библиотеку *.dll, подключаемую к программе. Если разработчик улучшит алгоритм прогнозирования, то пользо- вателям достаточно поменять только библиотеку *.dll, а вносить изменения в код, ответственный за интерфейс, вообще не придется.
Для создания библиотеки *.dll следует выбрать в меню пункт File ► New
► Project (шаблон Class Library). Далее в сгенерированный Visual Studio шаб- лон библиотеки следует добавить текст функции, которую требуется динамиче- ски подключать к программе. В листинге 6.1 приведен пример текста библио-
теки *.dll.
Листинг 6.1. Динамически подключаемая библиотека
using System;
using System.Collections.Generic;
using System.Text;
namespace ClassLibrary1
{
public class Class1
{
// текст функции, создаваемой программистом
public int summ(int i, int j)
{
// вычисляется сумма двух чисел
return i + j;
}
}
}
Для демонстрации возможности использования библиотеки *.dll созда-
дим программу, вызывающую функцию из этой библиотеки. Окно интерфейса программы приведено на рис. 6.1.
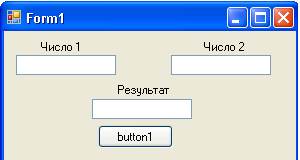
Рис. 6.1. Окно программы, использующей функцию из *.dllбиблиотеки
В этой программе два текстовых поля используются для ввода исходных слагаемых, третье для вывода результата работы функции. Текст программы, осуществляющий вызов библиотеки, приведен в листинге 6.2.
Листинг 6.2. Программа, использующая библиотеку *.dll
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data; using System.Drawing; using System.Text;
using System.Windows.Forms;
using ClassLibrary1; // Подключение библиотеки
namespace WindowsApplication6
{
public partial class Form1: Form
{
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
// создается обьект класа библиотеки *.dll
ClassLibrary1.Class1 meLib = new Class1();
// вызывается функция из библиотеки
int result=meLib.summ(Convert.ToInt16(textBox1.Text), Convert.ToInt16(textBox2.Text));
textBox3.Text = result.ToString();
}
}
}
Предварительно к приложению надо подключить используемую библио-
теку, выбрав в меню пункт Project ► Add Reference ► Browse.
6.3. Программа работы
Создайте интерфейс программы, обеспечивающий работу простейшего калькулятора (должны выполняться четыре арифметических действия). В за- висимости от варианта задания (табл. 6.1) дополнить реализацию программы вычислением следующих функций (их реализацию поместить в динамическую
библиотеку *.dll):
1. Нахождения гиперболического синуса sh(x)=(ex-e-x)/2.
2. Нахождения гиперболического косинуса ch(x)= (ex+e-x)/2.
3. Нахождения обратного гиперболического синуса arcsh(x)=ln(x+(x2+1)1/2).
4. Нахождения обратного гиперболического косинуса arcch(x)=ln(x+(x2-1)1/2).
5. Нахождения интегрального синуса
.
|

где γ=0.57721566 – постоянная Эйлера.
7. Нахождения интегрального гиперболического синуса
.
|
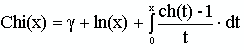 .
.
9. Нахождения факториала n!
10. Нахождения гиперболического тангенса th(x)=sh(x)/ch(x).
11. Нахождения интегральной показательной функции по ее разложению в ряд
.
|
|
13. Нахождения сочетаний n элементов по m
|
14. Нахождения корней квадратного уравнения.
15. Нахождения решения системы двух линейных уравнений с двумя неиз- вестными.