АЛГЕБРА И ГЕОМЕТРИЯ
Методические указания к изучению курса
и контрольные задания для студентов
заочной формы обучения направлений
230100.62 «Информатика и вычислительная техника» и
230400.62 «Информационные системы и технологии»
(1 семестр)
Брянск 2012
УДК 516.1/4
Алгебра и геометрия [Текст]+[Электронный ресурс]: методические указания к изучению курса и контрольные задания для студентов заочной формы обучения направлений 230100.62 «Информатика и вычислительная техника» и 230400.62 «Информационные системы и технологии» (1 семестр). – Брянск: БГТУ, 2012 – 22 с.
Разработал: к. т. н., доцент
А. П. Мысютин
Рекомендовано кафедрой “Высшая математика” БГТУ
(протокол №5 от 31.01.2012)
ПРЕДИСЛОВИЕ
Студенты первого курса заочной формы обучения направлений бакалаврской подготовки «Информатика и вычислительная техника» и «Информационные системы и технологии» в первом семестре должны выполнить две контрольные работы. В первой работе представлены задания по разделу «Линейная алгебра», а во второй − по разделу «Векторная алгебра».
Необходимые теоретические сведения из указанных разделов высшей математики и примеры решения типовых задач изложены в следующих учебных пособиях:
1. Беклемишев, Д.В. Курс аналитической геометрии и линейной алгебры /Д.В. Беклемишев. – М.: Физматлит, 2001. – 376 с.
2. Бугров, Я.С., Высшая математика в 2-х т. Т.1. Элементы линейной алгебры и аналитической геометрии./ Я.С. Бугров, С.М. Никольский. – М.: Дрофа, 2003.– 288 с.
3. Письменный, Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. − 2-е изд., испр. − М.: Айрис-пресс, 2002. – Ч. 1. − 288 с.
4. Данко, П.Е., Высшая математика в упражнениях и задачах / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. шк., 1999. – Ч. 1. – 304 с.
5. Ефимов Н.В. Краткий курс аналитической геометрии / Н.В. Ефимов. – М.: Физматлит, 2002. – 240 с.
Считая базовым учебник [3], укажем темы, которые необходимо изучить студенту для успешного выполнения контрольных работ.
Контрольная работа №1
Тема 1. Матрицы
1. Основные понятия. Литература: [3, §1, п. 1.1].
2. Действия над матрицами. Литература: [3, §1, п. 1.2].
Тема 2. Определители
1. Основные понятия. Литература: [3, §2, п. 2.1].
2. Свойства определителей. Литература: [3, §2, п. 2.2].
Тема 3. Невырожденные матрицы
1. Основные понятия. Литература: [3, §3, п. 3.1].
2. Обратная матрица. Литература: [3, §3, п. 3.2].
3. Ранг матрицы. Литература: [3, §3, п. 3.3].
Тема 4. Системы линейных алгебраических уравнений
1. Основные понятия. Литература: [3, §, п. 4.1].
2. Решение систем линейных уравнений. Литература: [3, §4, п. 4.2].
3. Матричный метод решения систем линейных уравнений. Формулы Крамера. Литература: [3, §4, п. 4.3].
4. Решение систем линейных уравнений методом Гаусса. Литература: [3, §4, п. 4.4].
5. Системы линейных однородных уравнений. Литература: [3, §4, п. 4.5].
Тема 5. Собственные векторы и собственные значения матриц
Литература: [4, гл. V, §4, п. 4].
Контрольная работа №2
Тема 1. Векторы
1. Основные понятия. Литература: [3, §5, п. 5.1].
2. Линейные операции над векторами. Литература: [3, §5, п. 5.2].
3. Проекция вектора на ось. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы. Действия над векторами, заданными проекциями. Литература: [3, §5, п. 5.3–5.5].
Тема 2. Скалярное произведение векторов
1. Определение скалярного произведения. Литература: [3, §6, п. 6.1].
2. Свойства скалярного произведения. Выражение скалярного произведения через координаты. Литература: [3, §6, п. 6.2, 6.3].
3. Некоторые приложения скалярного произведения. Литература: [3, §6, п. 6.4].
Тема 3. Векторное произведение векторов
1. Определение векторного произведения. Литература: [3, §7, п.7.1].
2. Свойства векторного произведения. Выражение векторного произведения через координаты. Литература: [3, §7, п. 7.2, 7.3].
3. Некоторые приложения векторного произведения. Литература: [3, §7, п. 7.4].
Тема 4. Смешанное произведение векторов
1. Определение смешанного произведения. Литература: [3, §8, п.8.1].
2. Свойства смешанного произведения. Выражение смешанного произведения через координаты. Литература: [3, §8, п. 8.2, 8.3].
3. Некоторые приложения смешанного произведения. Литература: [3, §8, п. 8.4].
Первая контрольная работа состоит из шести заданий. Вторая работа состоит из восьми заданий. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой номера его зачетной книжки. Заметим, что каждое задание 6 контрольной работы №1 включает в себя две задачи: а) и б). В контрольной работе №2 задание 7а выполняется только в вариантах 1–5, в остальных вариантах выполняется задание 7б.
Задания контрольной работы №1
1. Даны матрицы
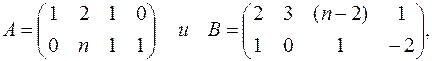
где n – номер варианта (n = 1,2,3,4,5,6,7,8,9,0). Найти значения a, при которых определитель матрицы А’В+aЕ равен нулю (А’ – транспонированная матрица для матрицы А, Е – единичная матрица 4-го порядка).
2. Решить систему линейных алгебраических уравнений по формулам Крамера, с помощью обратной матрицы и методом Гаусса.
Вариант 1. 
Вариант 2. 
Вариант 3. 
Вариант 4. 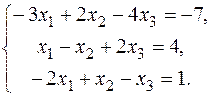
Вариант 5. 
Вариант 6. 
Вариант 7. 
Вариант 8. 
Вариант 9. 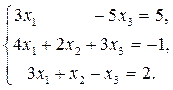
Вариант 0. 
3. Найти матрицу Х из уравнения.
Вариант 1
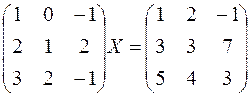 .
.
Вариант 2
 .
.
Вариант 3
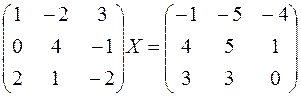 .
.
Вариант 4
 .
.
Вариант 5
 .
.
Вариант 6
 .
.
Вариант 7
 .
.
Вариант 8
 .
.
Вариант 9
 .
.
Вариант 0
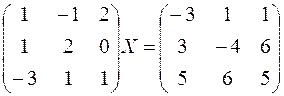 .
.
4. Найти ранг матрицы.
Вариант 1 Вариант 2
 .
. 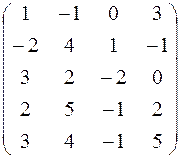 .
.
Вариант 3 Вариант 4
 .
.  .
.
Вариант 5 Вариант 6
 .
.  .
.
Вариант 7 Вариант 8
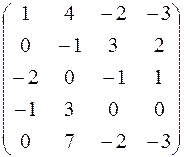 .
.  .
.
Вариант 9 Вариант 0
 .
.  .
.
5. Решить систему методом Гаусса.
Вариант 1 Вариант 2

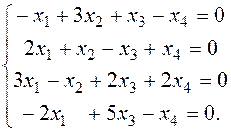
Вариант 3 Вариант 4

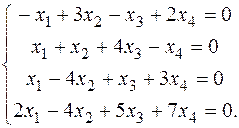
Вариант 5 Вариант 6


Вариант 7 Вариант 8


Вариант 9 Вариант 0

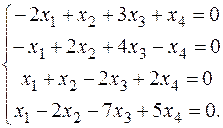
6. Найти собственные значения и собственные векторы матриц.
Вариант 1

Вариант 2

Вариант 3

Вариант 4


Вариант 5

Вариант 6

Вариант 7

Вариант 8

Вариант 9

Вариант 0

Вопросы к зачету (часть 1)
1. Что называется матрицей? Как определяются линейные операции над матрицами и каковы их свойства?
2. Что называется определителем? Каковы основные свойства определителей?
3. Что называется минором и алгебраическим дополнением?
4. Каковы способы вычисления определителей? Приведите примеры.
5. Что называется матрицей и расширенной матрицей системы линейных уравнений? Приведите примеры.
6. Что называется решением системы линейных уравнений? Какие системы называются совместными, а какие − несовместными?
7. Сформулируйте теорему Кронекера-Капелли.
8. Напишите формулы Крамера. В каком случае они применимы?
9. При каком условии система линейных уравнений имеет единственное решение?
10.Что можно сказать о системе линейных уравнений, если ее определитель равен нулю?
11.При каком условии однородная система n линейных уравнений с n неизвестными имеет ненулевое решение?
12.Опишите метод Гаусса решения и исследования систем линейных уравнений.
13.Какие неизвестные в системе линейных уравнений и в каком случае называются свободными, а какие − базисными? Что называется общим решением системы линейных уравнений?
14.Что называется рангом матрицы? Как его можно найти?
15. Что называется произведением двух матриц? Каковы свойства произведения матриц?
16. Какая матрица называется единичной?
17. Какая матрица называется обратной для данной матрицы? Всегда ли существует обратная матрица? Как можно найти обратную матрицу?
18. В чем состоит матричный способ решения систем линейных уравнений?
19. Что называется собственными значениями и собственными векторами матрицы?
20. Как найти собственные значения и собственные векторы матрицы?






