Вычисление статистических показателей вариационного ряда непосредственным способом

ПОСТРОЕНИЕ ВАРИАЦИОННЫХ РЯДОВ И ГРАФИЧЕСКОЕ ИХ ИЗОБРАЖЕНИЕ

Таблица 1.1−Выборочная статистическая совокупность (вариант № 2-3-9-15)

Номер столбца
d, cм	h, м	d, cм	h, м	d, cм	h, м	d, cм	h, м	d, cм	h, м	d, cм	h, м	d, cм	h, м	d, cм	h, м
16,5	20,8	30,0	24,2	21,5	20,0	26,5	25,5	22,0	22,8	26,1	23,0	23,5	22,6	17,5	20,0
22,0	22,2	24,3	23,8	10,5	12,0	20,0	20,5	23,0	22,8	27,0	21,0	30,0	25,7	23,0	24,1
28,5	24,1	23,0	23,0	24,5	25,3	22,0	19,7	25,0	24,5	24,1	20,0	16,5	20,8	26,4	24,7
15,0	18,9	22,7	22,1	10,5	15,0	17,0	18,8	22,0	21,8	18,0	16,0	30,0	24,2	18,0	19,0
21,1	22,1	22,3	23,4	30,0	25,0	19,0	17,8	25,0	20,0	22,5	19,1	21,5	20,0	22,5	23,7
21,0	21,8	25,0	24,0	22,0	23,5	17,5	20,0	16,4	17,0	21,2	22,2	26,5	25,5	24,0	23,0
23,0	24,1	26,4	24,7	18,0	19,0	22,5	23,7	22,7	22,0	24,0	18,0	22,0	22,2	28,5	24,0
24,0	23,0	28,5	24,0	22,0	22,5	23,0	23,5	27,5	24,9	13,0	14,7	24,3	23,8	22,0	22,0
16,0	19,4	32,0	25,0	24,0	22,5	18,0	20,3	25,0	24,0	11,5	14,0	10,5	12,0	23,0	23,5
21,8	21,6	27,0	24,0	23,5	23,0	28,0	23,1	13,0	16,4	13,0	15,7	20,0	20,5	16,0	19,4
30,0	25,5	21,5	23,0	22,0	21,0	24,5	24,2	24,0	21,8	35,0	22,0	28,5	24,1	32,0	25,0
36,0	26,5	31,0	25,0	27,5	24,5	13,0	18,7	12,5	14,0	22,3	22,4	23,0	23,0	24,0	22,5
19,0	20,0	21,5	23,9	30,5	27,5	27,0	24,0	10,5	15,0	20,0	20,0	24,5	25,3	18,0	20,3
24,0	25,4	19,0	18,7	20,5	19,8	20,0	21,6	24,0	21,8	19,0	20,4	22,0	19,7	21,8	21,6
36,0	26,0	18,0	16,7	32,0	27,0	21,5	22,4	20,0	21,0	19,5	18,0	15,0	18,9	27,0	24,0
21,0	19,0	30,0	25,0	11,0	12,0	14,0	18,6	19,0	20,5	10,0	11,4	22,7	22,1	23,5	23,0
19,0	19,5	33,5	26,0	26,0	23,4	16,0	18,9	20,0	19,0	12,5	14,0	17,0	18,8	30,0	25,5
19,5	17,7	29,0	24,2	21,5	22,5	28,0	23,0	20,0	20,2	30,0	25,0	21,2	22,1	21,5	22,0
21,5	22,0	32,0	25,3	24,5	24,2	18,0	17,2	17,0	18,7	29,5	25,3	22,3	22,4	22,0	21,0
28,5	27,0	17,5	19,7	36,0	29,5	24,0	21,8	29,5	26,4	13,0	15,5	30,0	25,0	24,5	24,2
29,0	23,4	10,0	10,4	25,5	22,3	19,0	18,3	20,5	20,1	15,0	16,0	19,0	17,8	36,0	26,5
20,3	21,8	20,0	21,3	21,0	20,6	28,5	26,0	17,5	21,0	8,0	7,8	21,0	21,8	31,0	25,0
24,5	22,4	24,5	22,0	22,0	26,0	17,5	18,7	27,1	22,4	22,0	20,1	25,0	24,0	27,5	24,0
18,0	18,5	12,5	13,5	30,0	26,0	22,5	22,5	26,0	23,3	19,0	17,8	22,0	22,5	13,0	18,7
15,0	18,3	23,0	22,5	13,0	14,5	22,0	23,8	15,0	16,1	28,0	24,5	10,5	15,0	28,0	23,1

Примечание. Выделены минимальные и максимальные значения диаметра и высоты.

i = (x_max − x_min) / k (1.1)

d_min = 8,0 см.;

d_max = 36,0 см.;

h_min = 7,8 м.;

h_max = 29,5 м.

i_d = (36,0 − 8,0) / 12= 2,33 ≈ 2 см.

i_h = (29,5 − 7,8) / 12 = 1,81 ≈ 2 м.

 

Таблица 1.2 − Разноска диаметров по интервалам

Интервалы, см.	Численность
Полная запись	Сокращенная запись	В рабочей записи	В цифрах
8,0- 9,9	8,0-	.
10,0- 11,9	10,0-
12,0- 13,9	12,0-
14,0- 15,9	14,0-
16,0- 17,9	16,0-	::
18,0- 19,9	18,0-
20,0- 21,9	20,0-
22,0- 23,9	22,0-
24,0- 25,9	24,0-
26,0- 27,9	26,0-
28,0- 29,9	28,0-	::
30,0- 31,9	30,0-	:.
32,0- 33,9	32,0-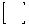
34,0- 35,9	34,0-	.
36,0- 37,9	36,0-	::
всего	−

 

Таблица 1.3 − Разноска высот по интервалам

Интервалы, м.	Численность
Полная запись	Сокращенная запись	В рабочей записи	В цифрах
7,0- 8,9	7,0-	.
9,0- 10,9	9,0-	.
11,0- 12,9	11,0-	::
13,0- 14,9	13,0-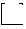
15,0- 16,9	15,0-
17,0- 18,9	17,0-	:

Продолжение таблицы 1.3

19,0- 20,9	19,0-	:
21,0- 22,9	21,0-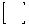
23,0- 24,9	23,0-
25,0- 26,9	25,0-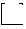
27,0- 28,9	27,0-	:.
29,0- 30,9	29,0-	.
всего	−

 

Таблица 1.4 − Вариационный ряд по диаметру

среднее значение интервала, см	9,0	11,0	13,0	15,0	17,0	19,0	21,0	23,0	25,0	27,0	29,0	31,0	33,0	35,0	37,0	всего
численность, шт
частость, %	0,5	4,5	5,0	3,0	7,0	9,5	14,0	18,0	12,5	7,5	7,0	6,5	2,5	0,5	2,0

 

Таблица 1.5 − Вариационный ряд по высоте

среднее значение интервала, м	8,0	10,0	12,0	14,0	16,0	18,0	20,0	22,0	24,0	26,0	28,0	30,0	всего
численность, шт.
частость, %	0,5	0,5	2,0	3,0	5,0	11,0	16,0	22,5	24,5	13,0	1,5	0,5

 

Таблица 1.6 − Распределение деревьев по диаметру и высоте

Интервалы диаметра х, см.	Интервалы высоты у, м.	Всего
7,0- 8,9	9,0- 10,9	11,0- 12,9	13,0- 14,9	15,0- 16,9	17,0- 18,9	19,0- 20,9	21,0- 22,9	23,0- 24,9	25,0- 26,9	27,0- 28,9	29,0- 30,9
8,0- 9,9
10,0- 11,9
12,0- 13,9
14,0- 15,9
16,0- 17,9
18,0- 19,9
20,0- 21,9
22,0- 23,9
24,0- 25,9
26,0- 27,9
28,0- 29,9
30,0- 31,9
32,0- 33,9
34,0- 35,9
36,0- 37,9
Всего

 

Таблица 1.7 − Суммарные численность и частость по диаметру

интервал, см.	численность, шт.	суммарная численность, шт.	суммарная частость, %
8,0 – 9,9			0,5
10,0 – 11,9			5,0
12,0 – 13,9			10,0
14,0 – 15,9			13,0
16,0 – 17,9			20,0

Продолжение таблицы 1.7

18,0 – 19,9			29,5
20,0 – 21,9			43,5
22,0 – 23,9			61,5
24,0 – 25,9			74,0
26,0 – 27,9			81,5
28,0 – 29,9			88,5
30,0 – 31,9			95,0
32,0 – 33,9			97,5
34,0 – 35,9			98,0
36,0 – 37,9

 

Таблица 1.8 − Суммарные численность и частость по высоте

интервал, м.	численность, шт.	суммарная численность, шт.	суммарная частость, %
7,0 – 8,9			0,5
9,0 – 10,9			1,0
11,0 – 12,9			3,0
13,0 – 14,9			6,0
15,0 – 16,9			11,0
17,0 – 18,9			22,0
19,0 – 20,9			38,0
21,0 – 22,9			60,5
23,0 – 24,9			85,0
25,0 – 26,9			98,0
27,0 – 28,9			99,5
29,0 – 30,9

 

частость, %

диаметр, см.

Рисунок 1.1 − Распределение частостей по диаметру

 

частость, %

высота, м.

Рисунок 1.2 − Распределение частостей по высоте

 

Рисунок 1.3 − Кумулята по диаметру

 

Рисунок 1.4 − Кумулята по высоте

ВЫЧИСЛЕНИЕ СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ ВАРИАЦИОННОГО РЯДА НЕПОСРЕДСТВЕННЫМ СПОСОБОМ

Таблица 2.1 − Вычисление статистических показателей непосредственным способом для диаметра

Диаметр xj, см.	Численность nj, шт.	xjnj	xj- M	(xj- M)2	(xj- M)2nj
9,0			-13,7	187,69	187,69
11,0			-11,7	136,89	1232,01
13,0			-9,7	94,09	940,90
15,0			-7,7	59,29	355,74
17,0			-5,7	32,49	454,86
19,0			-3,7	13,69	260,11
21,0			-1,7	2,89	80,92
23,0			0,3	0,09	3,24
25,0			2,3	5,29	132,25
27,0			4,3	18,49	277,35
29,0			6,3	39,69	555,66
31,0			8,3	68,89	895,57
33,0			10,3	106,09	530,45
35,0			12,3	151,29	151,29
37,0			14,3	204,49	817,96
Всего			−	−	6876,00

 

2.1 Среднее значение

М = ∑xjnj / ∑n (2.1)

М = 4530 / 200 = 22,65 ≈ 22,7 см.

2.2 Среднее квадратичное отклонение

σ = √ ∑(x_j − M)² n_j / ∑n (2.2)

σ = √ 6876/ 200 = √ 34,38 ≈ 5,86 см.

2.3 Основная ошибка среднего значения

m_M = σ / √ ∑n (2.3)

m_M = 5,86/ √200 ≈ 0,41 см.

M ± m_M = 22,7 ± 0,41см.

2.4 Коэффициент изменчивости

C = σ 100 / M (2.4)

C = 5,86 ∙ 100 / 22,7 = 25,8 %

Изменчивость средняя.

2.5 Точность опыта

p = m_M ∙ 100 / M (2.5)

p = 0,41 ∙ 100 / 22,7 = 1,8 % ≈ 2 %

2.6 Достоверность среднего значения

t₁ = M / m_{M (2.6)}

t₁ = 22,7 / 0,41 = 55

Среднее значение является достоверным.

2.7 Вычисление числа единиц наблюдения

n = С²x² / p² (2.7)

При вероятности 0,68 величина x = 1,0.

n = 665,64 ∙ 1 / 3,24 = 205

2.8 Вычисление медианы и моды вариационного ряда

Me = x_min + i (0,5N − ∑n) / n_{e (2.8)}

Сотая варианта находится в интервале 22,0 − 23,9 см.

x _min = 22,0 см.;

Величина интервала i = 2 см.;

Суммарная численность до интервала, где находится срединное значение, ∑n_j= 87;

Численность интервала, где находится срединное значение, n_e= 36.

Me = 22,0 + 2 ∙ (0,5 ∙ 200 − 87) / 36 ≈ 22,7 см.

суммарная численность, шт.

диаметр, см.

Рисунок 2.1 − Определение медианы графическим способом

По графику медиана равна 22,5 см.

Mo = 3Me − 2M (2.9)

Mo = 3 ∙ 22,7 − 2 ∙ 22,7 = 22,7 см.

 

Таблица 2.2 Вычисление статистических показателей непосредственным способом для высоты

Высота yj, м.	Численность nj, шт.	yjnj	yj- M	(yj- M)2	(yj- M)2nj
8,0			-13,5	182,25	182,25
10,0			-11,5	132,25	132,25
12,0			-9,5	90,25	361,00
14,0			-7,5	56,25	337,50
16,0			-5,5	30,25	302,50
18,0			-3,5	12,25	269,50
20,0			-1,5	2,25	72,00
22,0			0,5	0,25	11,25
24,0			2,5	6,25	306,25
26,0			4,5	20,25	526,50
28,0			6,5	42,25	126,75
30,0			8,5	72,25	72,25
Всего			−	−

 

М = 4302 / 200 = 21,51 ≈ 21,5 м.

σ = √ 2700 / 200 = √ 13,5 ≈ 3,67 м.

m_M = 3,67 / √200 ≈ 0,26 м.

M ± m_M = 21,5 ± 0,26 м.

C = 3,67 ∙ 100 / 21,5 = 17,1 %

Изменчивость средняя.

p = 0,26 ∙ 100 / 21,5 = 1,2 %

t₁ = 21,5 / 0,26 = 83

Среднее значение является достоверным.

При вероятности 0,68 величина x = 1,0.

n = 17,1² / 1,2² = 292,41 / 1,44 = 203

Сотая варианта находится в интервале 21,0 − 22,9 м.

y_min = 21,0 м.;

i = 2 м.;

∑n_j = 76;

n_e = 45.

Me = 21,0 + 2 ∙ (0,5 ∙ 200 − 76) / 45 ≈ 22,1 м.

суммарная численность, шт.

высота, м.

Рисунок 2.2 − Определение медианы графическим способом

По графику медиана равна 21,9 м.

Mo = 3 ∙ 22,1 − 2 ∙ 21,5 = 23,3 м.