Потоки с последействием (поток Эрланга)
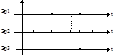 |
Поток Эрланга k-ого порядка – это поток случайныхсобытий, получающийся, если в простейшем случайном потоке сохранить каждое k-е событие, а остальные отбросить.

Рис. 1.4. Модель потока Эрланга
Просеивание событий начинает приводить к тому, что между точками появляется последействие (детерминация), которая тем выше, чем больше k.
Пусть 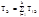 – интервал между событиями в потоке Эрланга k-го порядка, тогда
– интервал между событиями в потоке Эрланга k-го порядка, тогда 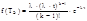 . 1.9)
. 1.9) 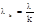 – интенсивность потока;l– интенсивность простейшего потока;
– интенсивность потока;l– интенсивность простейшего потока;
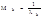 ;
; 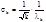 ,
,
Если M¹ s(в потоках с последействием равенство невозможно),
при k ® ¥ событие происходит строго в размеренное время, так как s ® 0.
Эр1: m = s– поток без последействия
Эрi: m ¹ s> 0– последействие i-ого порядка
Эр¥: m ¹ s= 0– регулярный поток
Порядок потока Эрланга – есть мера последействия потока.





 некоторым законом распределения (рис. 2.1).
Случайная величина x(ti) называется сечением случайного процесса, который полностью определяется законом распределения fi(x,ti). Моментные характеристики представляют собой неслучайные временные функции случайных процессов. Наиболее часто применяются математическое ожидание
некоторым законом распределения (рис. 2.1).
Случайная величина x(ti) называется сечением случайного процесса, который полностью определяется законом распределения fi(x,ti). Моментные характеристики представляют собой неслучайные временные функции случайных процессов. Наиболее часто применяются математическое ожидание 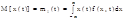 , (1) и дисперсия
, (1) и дисперсия
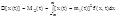 , (2)
, (2)
 Функции m1(t) и M2(t) не дают достаточно полного представления о характере случайного процесса. На рис. 2.2 схематически показаны процессы с разными математическими ожиданиями (рис. 2.2.а); с одинаковыми mx и my, но с различными дисперсиями (рис. 2.2.б); с одинаковыми mx, my и Dx, Dy (рис. 2.2.в). Но тем не менее процессы различаются: процесс y(t) изменяется быстрее, чем x(t), поэтому для дополнительной характеристики случайного процесса вводится понятие смешанной моментной функции второго порядка, называемой корреляционной (автокорреляционной):
Функции m1(t) и M2(t) не дают достаточно полного представления о характере случайного процесса. На рис. 2.2 схематически показаны процессы с разными математическими ожиданиями (рис. 2.2.а); с одинаковыми mx и my, но с различными дисперсиями (рис. 2.2.б); с одинаковыми mx, my и Dx, Dy (рис. 2.2.в). Но тем не менее процессы различаются: процесс y(t) изменяется быстрее, чем x(t), поэтому для дополнительной характеристики случайного процесса вводится понятие смешанной моментной функции второго порядка, называемой корреляционной (автокорреляционной):
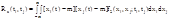 , (3)
где f2(xi, xj; ti, tj) - двумерная плотность распределения случайного процесса.Корреляционная функция характеризует статистическую связь между мгновенными значениями в различные моменты времени.При исследовании случайных процессов большое значение имеет стационарность, то есть неизменность их статистических характеристик во времени. Процессы, у которых плотности распределения инвариантны относительно t, т. е. fi(x, ti) = f(x) для всех сечений – стационарны в узком смысле; если неизменны только математические ожидания и корреляционные функции процессы стационарны в широком смысле. Стационарные случайные процессы могут обладать свойством эргодичности, если моментные характеристики для каждой реализации совпадают с соответствующими моментами, полученными для сечений.Для стационарных эргодических процессов математическое ожидание и дисперсия являются постоянными величинами, а корреляционная функция зависит только от сдвига
, (3)
где f2(xi, xj; ti, tj) - двумерная плотность распределения случайного процесса.Корреляционная функция характеризует статистическую связь между мгновенными значениями в различные моменты времени.При исследовании случайных процессов большое значение имеет стационарность, то есть неизменность их статистических характеристик во времени. Процессы, у которых плотности распределения инвариантны относительно t, т. е. fi(x, ti) = f(x) для всех сечений – стационарны в узком смысле; если неизменны только математические ожидания и корреляционные функции процессы стационарны в широком смысле. Стационарные случайные процессы могут обладать свойством эргодичности, если моментные характеристики для каждой реализации совпадают с соответствующими моментами, полученными для сечений.Для стационарных эргодических процессов математическое ожидание и дисперсия являются постоянными величинами, а корреляционная функция зависит только от сдвига  = tj+1- tj:
= tj+1- tj:
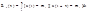 . (4)
График Rx(
. (4)
График Rx( ) приведен на рис. 2.3.
Автокорреляционная функции обладает следующими свойствами:
1. Четность, то есть R(
) приведен на рис. 2.3.
Автокорреляционная функции обладает следующими свойствами:
1. Четность, то есть R( )=R(-
)=R(-  ). 2. Rx(0)=D[x]. 3.
). 2. Rx(0)=D[x]. 3. 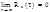 . 4.
. 4. 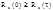 .
.

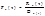 . (5)
. (5) справедливо неравенство
справедливо неравенство 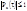 , поэтому такую величину иногда называют коэффициентом корреляции (хотя это и функция).
, поэтому такую величину иногда называют коэффициентом корреляции (хотя это и функция).
