В системах с ожиданием заявка, заставшая все каналы занятыми, не покидает систему, а становится в очередь и ожидает, пока не освободится какой-нибудь канал.
Т.е СМО с ожиданием подразумевает наличие буфера с очередью из заявок, заставших все каналы занятыми и ждущих освобождения одного из каналов. Если время ожидания заявки в очереди ничем не ограничено, то система называется «чистой системой с ожиданием». Если оно ограничено какими-то условиями, то система называется «системой смешанного типа». Это промежуточный случай между чистой системой с отказами и чистой системой с ожиданием.
Для практики наибольший интерес представляют именно системы смешанного типа.
Ограничения, наложенные на ожидание, могут быть различного типа. Часто бывает, что ограничение накладывается на время ожидания заявки в очереди; считается, что оно ограничено сверху каким-то сроком Tож, который может быть как строго определенным, так и случайным.
При этом ограничивается только срок ожидания в очереди, а начатое обслуживание доводится до конца, независимо от того, сколько времени продолжалось ожидание (например, в системах с коммутацией каналов после установления соединения между абонентами процесс разговора уже не прерывается).
В других задачах естественнее наложить ограничение не на время ожидания в очереди, а на общее время пребывания заявки в системе (например, при передаче SMS-сообщений, если после определенного количества попыток сообщение не доходит до адресата оно аннулируется).
Можно рассмотреть и такую смешанную систему, когда заявка становится в очередь только в том случае, если длина очереди не слишком велика. Здесь ограничение накладывается на число заявок в очереди (или на размер буфера m, рис. 6).
Рис. 6
В системах с ожиданием существенную роль играет так называемая «дисциплина очереди». Ожидающие заявки могут вызываться на обслуживание как в порядке очереди (раньше прибывший раньше и обслуживается), так и в случайном, неорганизованном порядке. Существуют СМО «с приоритетами», где некоторые заявки обслуживаются предпочтительно перед другими («генералы и полковники вне очереди»).
Одноканальная СМО с ожиданием и произвольным законом продолжительности обслуживания обозначается как М|G|1.
Предположим, что заявки обслуживаются в порядке их поступления. Состояния СМО нумеруются по числу заявок в СМО, находящиеся в очереди или обслуживаемых:
- СМО свободна (0); канал занят, очереди нет (1); канал занят, одна заявка стоит в очереди (2); канал занят и (к -1) заявок стоят в очереди.
Финальные вероятности для такой СМО существуют не всегда, а только тогда, когда система не перегружена. Если 
строго меньше единицы, то финальные вероятности существуют, при больше единицы очередь растет неограниченно, при =1 СМО справляется с потоком заявок только, если этот поток регулярный, а время обслуживания равно интервалу между заявками. Это идеальный случай, когда очереди вообще не будет. Но стоит только потоку заявок стать чуть-чуть случайным – и очередь уже будет расти до бесконечности.
Финальные вероятности состояний при меньше единицы:
; 
; 
Среднее число заявок в такой системе
Среднее время пребывания заявки в системе
Среднее число заявок в очереди
Среднее время пребывания заявки в очереди
Если обозначить через 
продолжительность обслуживания і -й заявки, тогда средняя продолжительность обслуживания 
, второй момент продолжительности обслуживания 
.
Здесь М{} означает математическое ожидание. Тогда в соответствии с формулой Поллачека-Хинчина [1, 2] среднее время ожидания заявки в очереди равно
, (21)
а средняя задержка заявки в СМО определяется по формуле
. (22)
Применяя теорему Литтла, получим выражения для среднего числа заявок в очереди на обслуживание 
и среднего числа заявок в системе 
:
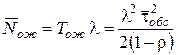; (23)
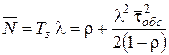. (24)
Если продолжительность обслуживания всех заявок одинакова, будем иметь СМО с детерминированным законом продолжительности обслуживания М|D|1, для которого характерно равенство 
. В результате получим
; 
. (25)
Пропускная способность системы с ожиданием, при тех же λ и µ, будет всегда выше, чем пропускная способность системы с отказами: в случае наличия ожидания необслуженными уходят не все заявки, заставшие n каналов занятыми, а только некоторые. Пропускная способность увеличивается при увеличении среднего времени ожидания.
