Основные понятия и классификация вычислительных процессов
При решении задачи на цифровой ЭВМ обычно выполняются следующие основные этапы:
· постановка задачи, где формулируется цель исследования и предъявляются требования к её решению по точности и времени;
· разработка математической модели решаемой задачи;
· выбор численного метода для приближённого решения задачи с учётом сформулированных требований;
· разработка вычислительного алгоритма;
· программирование, т.е. запись алгоритма решения задачи на определённом алгоритмическом языке;
· отладка программы;
· вычисление;
· обработка результатов вычисления.
Из перечисленных наиболее трудоёмкими являются четвёртый и пятый этапы, т.е разработка вычислительного алгоритма и программирование, поэтому им будет уделено особое внимание.
Под вычислительным алгоритмом понимается последовательная совокупность формализованных предписаний, переводящих исходные данные в процессе вычисления в искомые результаты.
К алгоритму задачи предъявляются следующие требования:
· детерминированность, т.е. алгоритм должен быть чётким, понятным и однозначным;
· массовость – возможность использования алгоритма для решения типовых задач;
· результативность, т.е. алгоритм должен состоять из конечного количества арифметических и логических действий, приводящих к искомому результату. Результативность во многом зависит от правильного задания исходных данных.
Алгоритм обычно задаётся в содержательном, блок-схемном или операторном виде. При блок-схемном описании вычислительного алгоритма следует пользоваться условными графическими обозначениями, приведенными на рис.1.

По принципу организации вычислений вычислительные процессы делятся на линейные и ветвящиеся.
Ветвящиеся процессы бывают с обратной связью, т.е. циклические, и без обратной связи, т.е. разветвляющиеся.
Циклом принято называть повторяемый участок вычислительного алгоритма.
Для организации циклических вычислительных процессов выделяется специальная переменная, называемая параметром цикла. По этой переменной ведётся управление счетом. В каждом цикле происходит изменение параметра цикла по определенной рекуррентной зависимости.
Различают циклические вычислительные процессы (ЦВП) известным (счетным) количеством повторений-циклов и с неизвестным количеством циклов.
Первые принято называть детерминированными ЦВП, а вторым – итерационными ЦВП.
В детерминированных ЦВП параметром цикла может быть аргумент функции или индекс элементов массива, а в итерационных ЦВП в качестве параметра цикла берется рассчитываемая функция, аргумент функции или индекс элементов массива. В двух последних случаях для итерационных циклов необходимо организовать комбинированное управление как по параметру цикла, так и по функции.
Перечисленные типовые вычислительные процессы являются составными частями комбинированных вычислительных процессов. В частности, из различного сочетания циклических вычислительных процессов организуются многоступенчатые циклы.
Линейные вычислительные процессы
Линейные вычислительные процессы (ЛВП) характеризуются последовательным выполнением операторов программы и блоков вычислительного алгоритма. ЛВП, как правило, являются составной частью циклического или разветвляющегося вычислительного процесса.
При освоении материала по разработке структурных схем сложную математическую зависимость целесообразно разбивать на отдельные части и оформлять их в виде самостоятельных блоков. Например, при вычислении функции по формуле
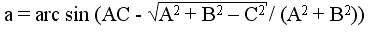
часть (фрагмент) вычислительного процесса А2 +В2 целесообразно оформить в виде самостоятельного блока.
При разработке вычислительного алгоритма целесообразно стремиться к минимизации количества вычислительных операторов и к минимальному использованию объема памяти, не ухудшая при этом точность вычисления выбранной последовательностью вычислительных действий. Например, степенной полином целесообразно вычислять по схеме Горнера:
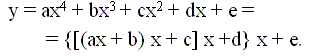
Используя известные методы тождественных преобразований, для вычисления функции r целесообразно выбрать следующую запись:







