Понятие множества
В математике встречаются самые разнообразные множества. Можно говорить о множестве граней многогранника, точек на прямой, множестве натуральных чисел и т.д. Понятие множества относится к числу первоначальных понятий, которые не определяются через другие, более простые. Вместо слова ''множество'' иногда говорят ''совокуп-ность'', ''собрание'' предметов и т.д. Предметы, составляющие данное множество, называются элементами данного множества.
Теория множеств посвящена в основном изучению именно бесконечных множеств. Теория конечных множеств называется иногда комбинаторикой.
Но простейшие свойства множеств, те, о которых мы только и будем здесь говорить, в большинстве случаев в равной мере относятся как к конечным, так и к бесконечным множествам.
Заметим, что в математике допускается к рассмотрению множество, не содержащее элементов – пустое множество. Запись а Î Х означает, что а есть элемент множества Х.
Определение. Множество В называется подмножеством множества А, если каждый элемент множества В является в то же время элементом множества А.
Каждый отдельный элемент множества А образует подмножество, состоящего из этого одного элемента. Кроме того, пустое множество является подмножеством всякого множества.
Подмножество множества А называется несобственным, если оно совпадает с множеством А.
Если множество В есть подмножество множества А, то говорим, что В содержится в А и обозначаем В Í А. Подмножество В множества А называется собственным подмножеством, если В не пусто и не совпадает с А (т.е. имеется элемент множества А, не содержащийся в В).
Операции над множествами
Пусть А и В – произвольные множества.
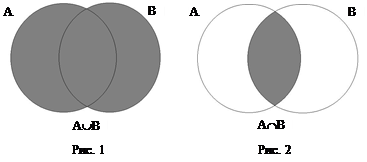
Определение. Объединением двух множеств А и В называется множество С = АÈВ, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В. (см. рис. 1).
Аналогично определяется объединение любого (конечного или бесконечного) числа множеств: если А i – произвольные множества, то их объединение 
есть совокупность элементов, каждый из которых принадлежит хотя бы одному из множеств А i.
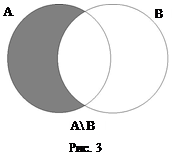
Определение. Пересечением множеств А и В называется множество С = АÇВ, состоящее из всех элементов, принадлежащих как А, так и В (см. рис. 2). Пересечением любого (конечного или бесконечного) числа множеств А i называется множество 
элементов, принадлежащих каждому из множеств А i.
Операции объединения и пересечения множеств по определению коммутативны и ассоциативны, т.е.
АÈВ = В È А, (А ÈВ) ÈС = А È (В È С),
А Ç В = В Ç А, (А Ç В) Ç С = А Ç (В Ç С).
Кроме того, они взаимно дистрибутивны:
(А È В) Ç С = (А Ç С) È (В Ç С), (1)
(А Ç В) È С = (А È С) Ç (В È С). (2)
Определение. Разностью множеств А и В называется множество тех элементов из А, которые не содержатся в В (рис. 3).
 |
Понятие функции. Отображение множеств
Пусть М и N – два произвольных множества.
Определение. Говорят, что на М определена функция f, принимающая значение из N, если каждому элементу x Î М поставлен в соответствие один и только один элемент y Î N. При этом М называется областью определения данной функции, а N – её областью значений.
Для множеств произвольной природы вместо термина «функция» часто пользуются термином «отображение», говоря об отображении одного множества в другое.
Если а элемент из М, то соответствующий ему элемент b = f (а) из N называется образом а при отображении f. Совокупность всех тех элементов а из М, образом которых является данный элемент b Î N, называется прообразом (или точнее полным прообразом) элемента b и обозначается f –1(b).
Пусть А – некоторое множество из М; совокупность { f (а): а Î А} всех элементов вида f (а), где а Î А, называется образом А и обозначается f (А). В свою очередь для каждого множества В из N определяется его полный прообраз f –1(В), а именно: f –1(В) есть совокупность всех тех элементов из М, образы которых принадлежат В.
Определение. Будем говорить, что f есть отображение множества М на множество N, если f (М) = N; такое отображение называют сюръекцией. В общем случае, т.е. когда f (М) Ì N, говорят, что f есть отображение в N. Если для любых двух различных элементов х 1 и х 2 из М их образы y 1 = f (x 1) и y 2 = f (x 2) также различны, то f называется инъекцией. Отображение f: М®N, которое одновременно является сюръекцией и инъекцией, называется взаимно однозначным соответствием между М и N.
