Министерство образования и науки Украины
Донецкий национальный технический Университет
Кафедра вычислительной
математики и программирования
ЗАДАНИЯ К К ЛАБОРАТОРНЫМ РАБОТАМ
по курсу «Информатика и системология»
для студентов специальности Экол
Утверждено на заседании каф. ВМиП
Протокол №1 от 30.08.2011
ДОНЕЦК, 2011
Построение графиков.
ЗАДАНИЕ 1. Изобразите график заданной функции.
| № | f(x) | № | f(x) | № | f(x) |

| 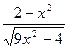
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
|
ЗАДАНИЕ 2. Изобразите линии заданные неявно в декартовых координатах.
| № | f(x) | № | f(x) | № | f(x) |

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 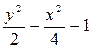
| 
| |||
| y 2 - 2 x 2 - 4 | y 2 +24 x 2 - 4 | 2 y 2 - 9 x 2 –18 | |||
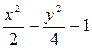
| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 4 y 2 - 5 x 2 – 20 | 
| |||

| 4 y 2 + 5 x 2 - 20 | 2 y2 +9 x 2 – 18 |
Решение нелинейных уравнений и систем.
ЗАДАНИЕ 1. Найти корни полинома.
| № | уравнение | № | уравнение | № | уравнение |

| 
| 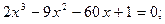
| |||

| 
| 
| |||

| 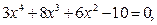
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 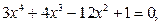
| 
| |||

| 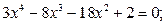
| 
| |||

| 
| 
|
ЗАДАНИЕ 2. Найти решение нелинейного уравнения.
| № | уравнение | № | уравнение | № | уравнение | № | уравнение |

| 
| 
| 
| ||||
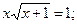
| 
| 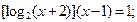
| 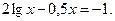
| ||||

| 
| 
| 
| ||||

| 
| 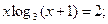
| 
| ||||

| 
| 
| 
| ||||

| 
| 
| 
| ||||
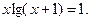
| 
| 
| 
|
ЗАДАНИЕ 3. Найти решение системы нелинейных уравнений.
| № | Система уравнений | № | Система уравнений | № | Система уравнений |

| 
| 
| |||
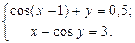
| 
| 
| |||

| 
| 
| |||

| 
| 
| |||

| 24- | 
| 
| ||

| 
| 
| |||

| 
| 
| |||

| 
| 
|
РАБОТА В MATHCAD.
Простейшие вычисления. Некоторые задачи матанализа.
ЗАДАНИЕ 1. Вычислить значение Х и Y по заданным формулам.
№1 
| №2 
| №3 
| №4 
| ||||||||||
| a | b | c | a | b | c | a | b | c | a | b | c | ||
| 3.456 | 0.642 | 7.12 | 8.64 | 1.25 | 66.4 | 3.845 | 4.632 | 0.562 | 0.2575 | 0.1756 | 0.2131 | ||
№5 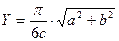
| №6 
| №7 
| №8 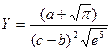
| ||||||||||
| a | b | c | a | b | c | a | b | c | a | b | c | ||
| 23.16 | 17.41 | 32.37 | 16.342 | 12.751 | 10.82 | 9.37 | 1.4 | 2.0435 | 1.1752 | 4.5681 | |||
№9 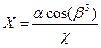
| №10 
| №11 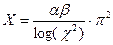
| №12 
| ||||||||||
| a | b | c | a | b | c | a | b | c | a | b | c | ||
| 3.456 | 1.245 | 0.327 | 0.143 | 0.242 | 3.258 | 0.3575 | 0.1756 | 0.2131 | 0.7568 | 0.8345 | 0.6384 | ||
№13 
| №14 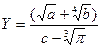
| № 15 
| № 16 
| ||||||||||
| a | b | c | a | b | c | a | b | c | a | b | c | ||
| 5.3 | 6.2 | 12.5 | 19.5 | 12.8 | 11.3 | 14.8 | 8.52 | 1.67 | |||||
№17 
| №18 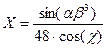
| № 19 
| №20 
| ||||||||||
| a | b | c | a | b | c | a | b | c | a | b | c | ||
| 2.48 | 3.05 | 1.73 | 2.878 | 1.169 | 0.299 | 2.76 | 3.25 | 17.67 | 0.652 | 0.131 | 0.144 | ||
№21 
| №22 
| № 23 
| № 24 
| ||||||||||
| a | b | c | a | b | c | a | b | c | a | b | c | ||
| 5.03 | 3.28 | 2.5 | 3.7 | 7.3 | 2.786 | 3.108 | 4.2 | 3.8 | |||||
Пример 1. Элементарные вычисления

Рис. 1.
ЗАДАНИЕ 2.. Вычислить производные и интегралы.
| № | Производную a¢(x) | Неопределенный интеграл | Определенный интеграл | Производную b¢¢(x) |
| 1,11 | 
| 
| 
| 
|
| 2,12 | 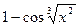
| 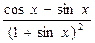
| 
| 
|
| 3,13 | 
| 
| 
| 
|
| 4,14 | 
| 
| 
| 
|
| 5,15 | 
| 
| 
| 
|
| 6,16 | 
| 
| 
| 
|
| 7,17 | 
| 
| 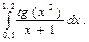
| 
|
| 8,18 | 
| 
| 
| 
|
| 9,19 | 
| 
| 
| 
|
| 10,20 | 
| 
| 
| 5x |
Пример 2. Вычисление производной.


Рис. 2
Пример 3. Вычисление интеграла.



Рис. 3
Решение задач линейной алгебры.
ЗАДАНИЕ. Решить систему уравнений 1) методом обратной матрицы и по правилам Крамера, сделать проверку. Систему уравнений 2) решить с помощью функции lsolve и решающего блока. Варианты заданий см. в работе №8.
Пример 4. Решить систему линейных уравнений при помощи правила Крамера[1]:

На рис. 4 приведен фрагмент рабочего документа, содержащий решение поставленной задачи.



Рис. 4.
Пример 5. Решить систему линейных уравнений из примера 4 методом обратной матрицы[2]. Решение показано на рис. 5.

Рис. 5.
Пример 6. Решить систему с помощью функции lsolve и при помощи решающего блока:
x 1+2 x 2+5 x 3=-9,
x 1– x 2+3 x 3=2,
3x 1–6 x 2– x 3=25.
Решение системы при помощи функции lsolve показано на рис. 6. Фрагмент рабочего документа на рис. 7 содержит пример применения решающего блока для решения системы.


Рис. 6 Рис. 7
Построение графиков на плоскости.
ЗАДАНИЕ. Построить графики функции f(x). Варианты заданий см. № 9.
Пример 7. Построить график функции y = x \(x 2–9). На рис. 8 изображен график заданной функции, которая терпит разрыв в точках 3 и –3.

Рис. 8
Пример 8. Построить график функции заданной неявно: 5 x 2+3 y 2–15=0.
Приведем уравнение к каноническому виду: x 2/3+ y 2/5=1. Разрешим уравнение относительно переменной у. Найдем область определения функции. Зададим ранжированную перемену и определим функции, описывающие верхнюю и нижнюю части эллипса. Построим график двух функций. Результат построения приведен на рис. 3.71.


Рис. 9
Решение нелинейных уравнений и систем.
ЗАДАНИЕ. Решить нелинейные уравнения и системы Варианты заданий см. в работе № 10.
Пример 9. Найти корни полинома 2 x 4–8 x 3+8 x2 –1=0.
Воспользуемся функцией polyroots(v), которая возвращает вектор всех корней (как вещественных, так и комплексных) полинома n –й степени, коэффициенты которого хранятся в массиве v, длиной n +1.
В нашем случае массив v следует определить как вектор столбец из пяти элементов[3](рис. 10). Решим задачу, так как показано на рис. 11. Найдем графическое решение заданного уравнения. Для этого создадим функцию F (x), определив полином как сумму произведений коэффициентов на x в соответствующей степени, и построим ее график. Точки пересечения графика с осью абсцисс и будут корнями уравнения. На рис. 12 видно, что графическое решение совпадает с аналитическим.



Рис. 10 Рис. 11 Рис. 12
Пример 15. Найти корни уравнения f (x)=0.
На рис. 13 видно, что график функции f (x) трижды пересекает ось абсцисс, то есть уравнение имеет три корня. Для решения этой задачи воспользуемся функцией root(F(x), x, a, b). Она возвращает с заданной точностью значение переменной x, при котором выражение F(x) равно нулю, a и b – пределы интервала изоляции корня. Понятно, что при такой форме записи функции нет необходимости задавать начальное значение x, так как оно определено в интервале [a,b][4].

Рис.13
Пример 16. Решить систему уравнений: { x 2+ y 2+3 x –2 y =4, x +2 y =5}.
Данная система легко сводится к одному уравнению при помощи элементарных преобразований (рис. 14). Линейное уравнение решается относительно одного из двух неизвестных, например, можно выразить х через у, выполнив команду Symbolic\Variable\Solve при выделенном х. Полученное выражение необходимо подставить в квадратное уравнение и упростить(Symbolic\Variable\Collect).
Решение квадратного уравнения с одним неизвестным, полученного в результате преобразований заданной системы, приведено на рис. 15. Графическое решение уравнение показало, что имеется два действительных корня. Поэтому решающий блок используется дважды с соответствующими начальными значениями.

Рис. 14.

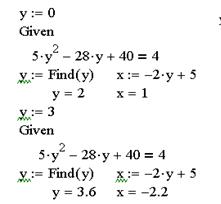
Рис. 15
На рис.16 показано, как решить систему с помощью решающего блока.

Рис. 16 
[1] Правило Крамера заключается в следующем. Если определитель ∆= det A матрицы системы из n уравнений с n неизвестными A∙x=b отличен от нуля, то система имеет единственное решение x1, x2,..., xn, определяемое по формулам Крамера xi=∆i/∆, где ∆i – определитель матрицы, полученной из матрицы системы А заменой i –го столбца столбцом свободных членов b.
[2] Метод обратной матрицы: для системы из n линейных уравнений с n неизвестными A∙x=b, при условии, что определитель матрицы А не равен нулю, единственное решение можно представить в виде x=A-1∙b.
[3] Обратите внимание, что в уравнении отсутствует переменная x в первой степени. Это означает, что соответствующий коэффициент равен нулю.
[4] Обратите внимание на последнее обращение к функции root на рис.3.78. MathCAD выдал сообщение об ошибке: «Значения на обоих концах интервала должны иметь противоположные знаки». Произошло это потому, что интервал изоляции задан неверно. На графике видно, что на концах этого интервала функция знак не меняет.






