Описание программы-функции

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

 

УТВЕРЖДАЮ

Директор ИК

_____________ М.К.Сонькин

 

«____»_____________2011 г

 

Т.Е. Мамонова

 

 

Лабораторная работа № 5

 

ПРОГРАММИРОВАНИЕ В MATHCAD

 

Методические указания по выполнению лабораторных работ

по курсу «Информационные технологии» для студентов I курса,
обучающихся по направлениям:

220700 «Автоматизация технологических процессов и производств»,

221000 «Мехатроника и робототехника»

 

 

Издательство

Томского политехнического университета

 

УДК 519.6

ББК 00000

А00

 

Мамонова Т.Е.

А00 Программирование в MathCAD. Методические указания по выполнению лабораторных работ по курсу «Информационные технологии» для студентов I курса, обучающихся по направлениям 220700 «Автоматизация технологических процессов и производств»,221000 «Мехатроника и робототехника» / Т.Е. Мамонова. – Томск: Изд-во Томского политехнического университета, 2011. – 22 с.

УДК 519.6

ББК 00000

 

Методические указания рассмотрены и рекомендованы к изданию методическим семинаром кафедры интегрированных

компьютерных систем управления ИК

«13» января 2011 г.

 

Зав. кафедрой ИКСУ

доктор технических наук _________________ А.М. Малышенко

 

 

Председатель учебно-методической

комиссии _________________ В.Н. Шкляр

 

 

Рецензент

Доцент ИКСУ ИК НИ ТПУ кандидат технических наук

В.Н. Шкляр

 

© ГОУ ВПО «Томский политехнический

университет», 2011

© Мамонова Т.Е., 2011

© Оформление. Издательство Томского

политехнического университета, 2011

 

ЛАБОРАТОРНАЯ РАБОТА № 5

Программирование в MathCAD

Цель работы: приобрести навыки программирования, изучить реализацию основных принципов программирования в математическом пакете MathCAD.

Теоретическая часть

Функции являются важнейшим инструментом математики. В лабораторной работе № 1 представлена технология работы с пользовательскими функциями, которые можно описать с помощью одного выражения. Если описания функции нельзя уместить в одно выражение, то без элементов программирования обойтись сложно.

Язык программирования MathCAD содержит все элементы языка высокого уровня, необходимые для математических расчетов. Будучи дополненным сотнями встроенных функций и операторов системы, возможностями численного и символьного расчета различных величин, он по эффективности не уступает профессиональным системам программирования. Кроме того, у него есть одно очень крупное преимущество: язык программирования MathCAD предельно прост (а по изящности и наглядности в оформлении алгоритмов вообще не имеет аналогов).

Как правило, при использовании функций, встроенных в систему MathCAD, пользователи не задумываются о том, на основании каких методов и решений достигается цель, поставленная перед функцией. Такая встроенная функция используется по типу «черного ящика» – пользователь познакомился с ее описанием/спецификацией, вызвал для решения, получил ответ.

При программировании пользовательских функций будем придерживаться «созвучного» порядка, т.е. идти от спецификации к программированию.

Спецификация функций

Спецификация функции состоит из ее заголовка и описания назначения – выходного значения или результата работы функции. Для примера можно обратиться к мастеру функций и более внимательно посмотреть на предоставляемые им для его функций описания. На рис. 1 открыта страница со спецификацией функции rnorm.

Заголовок содержит имя функции (rnorm) и список формальных параметров (m, mu, sigma). Каждая пользовательская программа – функция MathCAD должна иметь оригинальное имя, используя которое будет осуществляться обращение к этой программе-функции. Через это же имя (и только через это имя) «возвращается» в рабочий документ результат выполнения программы-функции.

Через формальные параметры «внутрь» программы-функции «передаются» данные, необходимые для выполнения вычислений внутри программы. В качестве формальных параметров могут использоваться имена простых переменных, массивов и функций. Формальные параметры отделяются друг от друга запятой.

Рис. 1. Спецификация функций, представляемая мастером функций

 

При описании назначения функции необходимо сказать, что возвращает функция в качестве своего результата (в описываемой функции rnorm возвращает вектор нормально распределенных случайных значений). При этом обязательно нужно пояснить роль каждого из формальных параметров, перечисленных в заголовке (m – количество значений, mu – среднее значение, sigma – стандартное отклонение).

Программирование функций

Для написания программ-функций в системе MathCAD предусмотрена специальная панель программировав – Programming (Программирование), содержащая все операторы и элементы языка.

Общий вид панели Programming представлен на рис. 2. Операторы в программу вставляются только с помощью кнопок этой панели.

Назначение основных команд, представленных на панели:

Add Line – добавление новой строки в программу или создание заготовки программы из двух строк, если программы еще не существует;

← – присвоение значения локальной переменной;

if – условный оператор. Позволяет в зависимости от условия выполнять или не выполнять те или иные действия;

otherwise – используется сразу после оператора if и позволяет выполнить определенные действия при невыполнении условия в операторе if;

for – оператор создания цикла со счетчиком;

while – оператор создания цикла, выполнение которого продолжается до тех пор, пока выполняется указанное условие. continue – продолжить вычисления в цикле;

 

Рис. 2. Вид панели инструментов Programming (Программирование)

 

break – прервать вычисления в цикле;

return – оператор возврата;

on error – оператор перехода при возникновении ошибки.

Чтобы написать программу, прежде всего для нее должен быть соз­дан специальный, обособленный от остального документа, программный блок →тело функции. Выглядит он как черная вертикальная линия с маркерами, в которые заносятся те или иные выражения и операторы алгоритма. Чтобы построить единичный элемент программного блока, нажмите кнопку команды Add Line (Добавить линию) панели Programming (Программирование).

Присваивание значений в программах имеет ряд особенностей. Важнейшим из них является то, что присвоение величин используемым алгоритмом функциям и переменным может быть произведено как в самой программе, так и выше нее. Данные два подхода весьма существенно разнятся:

• Если значение переменной или функции присваивается в программе посредством оператора, то такая переменная или функция будет являться локальной. То есть она будет видимой только в рамках программы. Как-то повлиять на объекты вне программы она не сможет (равно, как извне к ней нельзя будет получить доступ).

Если переменная или функция задается выше программы с по­мощью оператора «:=», то она в программе будет обладать глобальной видимостью. То есть такая переменная или функция будет доступна любому нижележащему объекту, в том числе и коду программ. Однако программа может только прочитать значение глобальной переменной или вызвать глобальную функцию. Изменить каким-либо образом значение глобальной переменной или функции программа не может. Это очень важно учитывать при написании алгоритмов.

• Если программа должна осуществлять какую-то модификацию объекта, то результат своей работы она должна возвращать.

Все программы, составляемые в пакете MathCAD, с точки зрения любого языка программирования (например, Turbo Pascal) представляют собой подпрограммы – функции, которые могут возвращать в качестве результата число, вектор или матрицу.

Описание программы-функции

Перед тем как использовать программу-функцию нужно ее описать. Описание программы-функции размещается в рабочем документе перед вызовом программы-функции и включает в себя заголовок функции и тело функции, соединенные в единое целое с помощью операции присваивания («:=»).

Заметим, что если программа используется для вычисления одного значения, то в своем заголовке она не содержит списка формальных параметров и называется программой-скаляром.

Программа-функция может не иметь формальных параметров и тогда, когда данные передаются через имена переменных, определенных выше описания программы-функции. Эти переменные будут являться глобальными для данной функции.

Технология создания программы -функции в рабочем документе MathCAD состоит из следующих шагов:

1. Ввести заголовок функции.

2. Ввести знак присваивания «: =».

3. Выполнить команду Add line, расположенную на панели Programming (Программирование). Появившейся на экране шаблон с вертикальной чертой и полями для ввода операторов будут составлять заготовку для тела программы-функции.

4. Вписать операторы в шаблон-заготовку. Тело программы-функции может включать любое число операторов: локальных операторов присваивания, условных операторов и операторов цикла, а также вызов других программ-функций.

5. Самоенижнее поле всегда предназначено для определения возвращаемого программой значения.

 

Практическая часть

Пример 1. Требуется подготовить описание функции ,вычислить значения этой функции при х = 4.15 и g = 1.854.

Решение. Заметим, что при вычислении y можно обойтись без описания и использования пользовательской функции и тем более без программирования, как это показано на рис. 4, а. Использование функции следует из требования к задаче для простоты изложения. Для нахождения значения функции «внутрь» программы-функции следует передать значения х и g, необходимые для выполнения вычислений внутри программы. Поэтому переменные х и g следует включить в список формальных параметров заголовка создаваемой функции. Назовем эту функцию – у. Тогда подготовка описания функции, и ее выполнение в соответствии с описанной технологией могут быть выполнены, как это представлено на рис. 3.

 

Рис. 3. Пошаговое создание и выполнение программы-функции

В данном примере введена вспомогательная локальная переменная t для вычисления значения функции. И эта переменная расположена в последней строчке программного блока. В пункте (6) приведена операция вычисления функции для фактических значений. На рис. 4, b, с приведены другие варианты решения поставленной задачи.

Рис. 4. Демонстрация элементов программирования простых выражений

В примере, представленном на рис. 4, в первой колонке a для вычисления значения 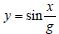используется базовый набор средств без элементов программирования. Во второй b и третьей c колонках производятся точно такие же вычисления, но с использованием элементов программирования. Обе программы (b и с) можно считать эквивалентными, так как возвращают они одно и то же значение, которое располагается в последней строчке программируемой части. В (b и с) мы имеем дело с программой – скаляром, так как они используются для вычисления одного значения и не имеют формальных параметров.

Внутри программ (b и с) используются глобальные переменные g и – из документа. Значения этих переменных определены заранее. Обе программы из примера, представленного на рис. 4, в своей программируемой части содержат операторы присваивания с использованием локальных переменных. Переменные, созданные внутри программы с таким видом присваивания, являются внутренними, и доступ к ним может осуществляться только в самой программе.

1. В программной части используются глобальные переменные обычно только как операнды в выражениях.

2. Присвоить глобальным переменным значения внутри программы можно только локальным образом. После выхода из программы эти переменные сохраняют свои «глобальные» значения.

3. Использование «обычного» оператора присваивания «:=» в теле программы-функции приводит к синтаксической ошибке.

4. Последняя строка программы не должна содержать управляющих операторов. Эта строка задает значение, возвращаемое программой, т.е. получает результат вычислений и может содержать имя локальной переменной результата (рис. 4, с) или выражение, вычисляющее результат (рис. 4, b).

5. Обычно программа содержит больше чем две строки, поэтому рекомендуется сразу задавать блок из 5-6 маркеров.

6. Добавление недостающих полей для ввода дополнительных операторов производится с помощью кнопки Add line панели программирования. При этом поле ввода добавляется внизу выделенного к этому моменту оператора.

7. Для удаления того или иного оператора или поля ввода из тела программы-функции, нужно заключить его выделить и нажать клавишу <Delete>.

8. Программный блок можно создать и внутри уже заданного блока (вложенный блок). Для этого следует использовать один из стандартных способов: поставить курсор в маркер соответствующего оператора программирования и выполнить Add line.

9. Иногда при написании программы бывает нужным добавить строку к уже созданному блоку. Чтобы это сделать, поставьте курсор в ту строку блока, выше или ниже которой должна быть введена строка, и нажмите клавишу <Пробел>. При этом строка будет выделена и можно будет произвести добавление одним из стандартных способов.

10. Положение вставляемого маркера определяется положением вертикальной черты курсора. Если она находится слева от выделенного выражения, то маркер будет добавлен выше выделенной строки, если справа – то ниже.

11.Чтобы развернуть курсор в нужную сторону, нажмите клавишу <Insert>.

12.Чтобы добавить строку к целому блоку, его следует выделить, дважды нажав клавишу <Пробел>.

13.В том случае, если программа содержит блоки различных уровней, то для добавления строки, например, к первому блоку, нажмите клавишу <Пробел> несколько раз: при каждом нажатии будут выделяться блоки более низкого уровня.

Пример 2. Требуется найти действительные корни квадратного уравнения ax² + bx + с = 0, где a, b, с – любые действительные числа и . Известно, что в зависимости от знака дискриминанта d = b² - 4ас действительные корни уравнения могут быть получены по формуле:

Блок-схема этого алгоритма показана на рис. 5.

 

Рис. 5. Блок-схема вычисления действительных корней квадратного уравнения

 

Решение. Опишем вычисление корней в виде программы-функции. Функция R(a,b,c) возвращает значения действительных корней квадратного уравнения a∙x² + b∙x + с = 0 или сообщает о том, что уравнение не имеет корней. Здесь a, b, с – коэффициенты уравнения.

Очевидно, что в данном случае мы имеем дело с ветвящимся процессом.Программирование ветвящихся процессов требует проверки некоторых условий, в зависимости от которых выбирается вычислительная формула. Для реализации таких вычислений на панели программирования предусмотрен оператор if (если).

Условный оператор if

1. При включении оператора if в блок программирования появляется шаблон с двумя полями ввода – справа и слева от оператора: ■ if ■.

2. В поле ввода справа от оператора записывается условие. Для ввода условий следует использовать панель Boolean (Логические), где есть кнопки для проверки условий (= > < ≤ ≥ *).

3. В поле ввода слева нужно ввести строку программы (или несколько строк), которая будет выполняться, если введенное условие истинно.

4. Если невыполнение условия должно привести к выполнению какой-либо другой строки (или нескольких строк), то можно в строке, следующей за оператором if, вставить оператор otherwise (иначе). В поле ввода слева от этого оператора надо ввести строку, которая будет выполняться только в том случае, если условие ложно.

5. Чаще всего оператор if используется для задания разрывных или кусочно-непрерывных функций.

Описание функции и примеры ее вызова представлены на рис. 6.

Рис. 6. Описание функции R(a,b,x), предназначенной для вычисления корней квадратного уравнения

 

Пример 3. Требуется подготовить описание программы-функции

и построить ее график на интервале [-2, 4].

Решение. Из анализа аналитического выражения функции y видно, что функцияявляется кусочно-непрерывной на числовой оси и алгоритм вычислений содержит три ветви. Вычисление значения y зависит от местоположения переменной x на числовой оси.

Для нахождения значения функции целесообразно ввести один формальный параметр, соответствующий переменной x. Функция f(x) возвращает значение функции, определенной в соответствии с условием примера 3. Здесь х - аргумент для вычисления.

В описании функции требуется проверить три условия. В зависимости от результатов проверки этих условий применяется соответствующая условию вычислительная формула. Поэтому при программировании можно с проверкой каждого из условии связать условный оператор if, как это показано на рис. 7. А можно ограничиться проверкой двух условий и оператором otherwise, учитывая тот факт, что функция задана на всей числовой оси, и исключение двух условий оставляет выполнение третьего условия. На рис. 8 представлен второй вариант функции-программы.

Рис. 7. Демонстрация элементов программирования ветвящихся процессов

Рис. 8. Демонстрация элементов программирования ветвящихся процессов

На рис. 9 представлены примеры программ-функций, реализующих вычисления, содержащие ветвящиеся процессы.

Рис. 9. Примеры программирования функций с проверкой условий.

Здесь x – глобальная переменная

 

Пример 4. Требуется найти максимальный и минимальный элементы в заданном массиве.

Решение. Задача поиска наибольшего/наименьшего значений в заданном массиве относится к типовым циклическим алгоритмам, на рис.10 и 11 приведены блок-схемы этих алгоритмов.

Рис. 10. Блок-схема алгоритма Рис. 11. Блок-схема алгоритма

нахождения наибольшего значения нахождения наименьшего значения

Спецификацию для этой функции можно записать следующим образом:

Функция Fun (P) возвращает наибольшее и наименьшее значение в массиве Р.

Для создания циклов в MathCAD предусмотрено два оператора: for и while. Поскольку количество повторений цикла заранее известно и связано с числом элементов заданного массива, в данном решении целесообразно использовать оператор for.

Циклы с оператором for.

1. После вставки оператора for в строку программы его сопровождают три поля ввода, как это показано на рис. 12.

Рис. 12. Шаблон оператора циклаfor

 

2.В поле ввода после слова for следует указать имя переменной-счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения.

3. В поле ввода после знака следует указать диапазон значений, которые будет принимать переменная-счетчик. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В таком случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Количество повторов цикла будет равно количеству элементов массива.

4. В поле ввода под словом for следует ввести тело цикла

Обозначим имя переменной-счетчика, которая используется в операторе for – буквой t. Для описания алгоритма воспользуемся тем, что в операторе цикла для переменной-счетчика можно указать в качестве диапазона имя массива. Как сказано выше, в таком случае переменная t будет последовательно принимать значения всех элементов указанного в for массива (в нашем случае – это массив Р). Для обозначения максимального и минимального значений в программу введем две вспомогательные переменные Pmax и PMin. Тогда описание функции может быть представлено в виде, как это показано на рис. 13.

Отметим, что в данном случае в качестве результата работы функции нужно вернуть два значения, а специфика функции в MathCAD такова, что она позволяет вернуть только одно значение, но при этом сказано, что функция в качестве результата может вернуть, в том числе, вектор и матрицу. Поэтому при формировании результата мы определим его как вектор из двух значений.

Справа от программы-функции, представленной на рис. 13, написаны операторы, предназначенные для создания вектора с именем U из шести элементов. Для этого введена вспомогательная переменная i, задающая диапазон изменения индекса массива, а значения элементов массива U формируются с помощью функции rnd – датчика случайных чисел. Параметр 20 в ней определяет диапазон принимаемых значений.

На рис. 14, a представлен второй вариант программы-функции, в котором в качестве диапазона значений для переменной-счетчика цикла for берется диапазон изменения индекса массива. Поэтому в список формальных параметров в заголовок функции вносится еще один параметр n, который указывает верхнюю границу изменения индекса.

 

Рис. 13. Описание и использование функции Fun (P)

Рис. 14. Описание и использование функции Fun (P)

 

Пример 5. Требуется определить функцию, предназначенную для вычисления приближенного значения квадратного корня из числа N по формуле Ньютона:

где x ₀ – заданное начальное приближение корня.

Решение. Алгоритм решения задача подробно рассмотрен в главе 1, блок-схема алгоритма представлена на рис. 15. Поэтому остановимся только на спецификации программы-функции, и ее описании.

Рис. 15. Блок-схема вычисления приближенного значения

квадратного корня из числа N

Спецификацию для этой функции можно записать следующим образом:

Функция Fun (N, s, x ₀) возвращает значение квадратного корня из числа N с заданной точностью вычислением – s и заданным начальным приближением корня – x ₀.

Анализ блок-схемы показывает, что в представленном циклическом процессе количество повторений цикла заранее неизвестно и напрямую зависит от точности вычислений. Поэтому пользоваться оператором for не является целесообразным. Для таких циклических процессов предусмотрен оператор цикла while.

1. После вставки этого оператора в строку программы его сопровождают два поля ввода, как это показано на рис. 16.

Рис. 16. Шаблон оператора циклаwhile

6. В поле ввода ниже слова while следует ввести тело цикла – одна или несколько строк программы, выполнение которых нужно повторить несколько раз.

7. В поле ввода справа от слова while следует ввести условие. Оно будет проверяться после каждого выполнения тела цикла и в тот момент, когда условие перестанет выполняться, повторение тела цикла прекратится.

Из описания оператора цикла следует, что условие повторения цикла записывается справа от слова while, а повторяемая часть цикла должна располагаться ниже конструкции while, а в описанной блок-схеме один из повторяемых операторов, а именно оператор, в котором вычисляется значение х, располагается до блока с условием повторения. Чтобы согласовать действия в блок-схеме с действиями оператора, сделаем перестановку – поставим определение переменной х после блока- условия. А для проверки условия введем вспомогательную переменную R, и для того, чтобы на начальном этапе пройти внутрь цикла для вычислений, определим начальное значение этой переменной значением, большим, чем указанная точность, например, значением, равным 1. И тогда функция может быть представлена в виде, как это показано на рис. 17.

Рис. 17. Описание и использование функции, предназначенной для извлечения квадратного корня

Пример 6. Требуется определить функцию, которая будет изменять значения элементов матрицы A(n х m), имеющей n строк и m столбцов следующим образом: заменить все неотрицательные элементы нулем, а отрицательные – единицей.

Решение. Алгоритм решения задача подробно рассмотрен, блок-схема алгоритма представлена на рис. 18.

Рис. 18. Блок-схема к примеру 6

 

Поэтому остановимся только на спецификации программы-функции, и ее описании. Спецификацию для этой функции можно записать следующим образом:

Функция Fun(a,n,m) возвращает преобразованную матрицу a(nxm) по правилу: все неотрицательные элементы заменяются нулем, а отрицательные – единицей.

Анализ алгоритма показывает, что в данном случае мы имеем дело с двумя вложенными циклами, в которых переменные i и j могут играть роль переменных-счетчиков операторов цикла типаfor. Очевидно, что в качестве диапазона значений для этих переменных берется диапазон изменения индекса массива. На рис. 19 приведено определение функции. Описанная функция вызывается для изменения матрицы D, причем, измененная матрица заносится в матрицу T.

Рис. 19. Описание и использование функции, предназначенной

для преобразования матрицы

Рекомендуемая последовательность действий при разработке программ-функций:

1. Подготовить спецификацию функции.

2. Разработать алгоритм решения.

3. Установить, какие переменные помимо формальных параметров (локальные, глобальные переменные) понадобятся для реализации алгоритма.

4. Описать алгоритм словами или в виде блок-схемы.

5. Описать алгоритм в виде программы-функции на языке MathCAD.

Контрольные вопросы

1. Технология создания программы-функции в рабочем документе MathCAD.

2. Опишите последовательность действий при реализации условного перехода в программном модуле.

3. Опишите последовательность действий при реализации циклов в программном модуле.

4. Какие операции выполняются при создании вложенного программного модуля?

5. Для каких действий предназначены ключевые слова: otherwise, return, error в MathCAD?

6. Как осуществляется вызов функции в MathCAD?

7. Создайте инструкцию для работы с break и continue.

8. Запишите оператор внутреннего присваивания, используемый в теле программы.

9. Укажите отличительные особенности программы-скаляра.

10. Последовательность действий, выполняемых чтобы добавить строку к целому блоку.

Варианты заданий к лабораторной работе № 5

Задание 1. Подготовить описание функции, заданной в соответствии с вариантом, вычислить значения этой функции при x ₁ и x ₂

Вариант 1.

,

x ₁=-2.34; x ₂ = 5.65

 

Вариант 2.

,

x ₁=0.564; x ₂ = 12.43

 

Вариант 3.

,

x ₁=-43.67; x ₂ = 5.09

 

Вариант 4.

,

x ₁=-100.87; x ₂ = 25.769

 

Вариант 5.

,

x ₁=0.787; x ₂ = 76.091

 

Вариант 6.

,

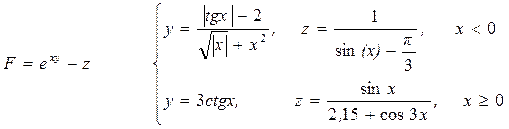x ₁=-87.134; x ₂ = 12.454

 

Вариант 7.

,

x ₁=0.0765; x ₂ = 543.87

 

Вариант 8.

,

x ₁=-987.76; x ₂ = 43.78

 

Вариант 9.

,

x ₁=0.436; x ₂ = 21.677

 

Вариант 10.

,

x ₁=-564.876; x ₂ = 0.333

Задание 2. Требуется определить функцию, которая выполняет представленные в вариантах задания.

Вариант 1. Дана последовательность из n целых чисел. Найти количество элементов этой последовательности, кратных числу 2 и не кратных числу 3.

Вариант 2. Дана последовательность n целых чисел. Найти количество четных элементов этой последовательности.

Вариант 3. Дана последовательность n целых чисел. Найти сумму минимального и максимального элементов в этой последовательности.

Вариант 4. Дана последовательность n целых чисел. Найти максимальный элемент в этой последовательности.

Вариант 5. Дана последовательность n целых чисел. Найти номер минимального элемента в этой последовательности.

Вариант 6. Дана последовательность n целых чисел. Найти сумму элементов с нечетными номерами из этой последовательности

Вариант 7. Дана последовательность n целых чисел. Найти сумму нечетных элементов этой последовательности.

Вариант 8. Дана последовательность n целых чисел. Найти сумму элементов с четными номерами из этой последовательности.

Вариант 9. Дана последовательность из n целых чисел. Найти сумму элементов с четными номерами из этой последовательности.

Вариант 10. Дана последовательность из n целых чисел. Найти количество элементов этой последовательности, кратных числу К.

Содержание отчета

· Титульный лист (Приложение Г).

· Цель работы.

· Задание.

· Листинг документа MathCAD.

· Ответы на контрольные вопросы.

· Выводы по работе.

Список литературы

1. Плис, Александр Иванович. MATHCAD 2000; Математический практикум для экономистов и инженеров: учебное пособие для вузов / А. И. Плис, Н. А. Сливина. – М.: Финансы и статистика, 2000. – 656 с.

2. Глушаков, Сергей Владимирович. Математическое моделирование MathCAD 2000, MatLab 5: Учебный курс / С. В. Глушаков, И. А. Жакин, Т. С. Хачиров. – Харьков; М.: Фолио: АСТ, 2001. – 524 с.

3. Дьяконов, Владимир. Mathcad 2000: Учебный курс / В. Дьяконов. – СПб.: Питер, 2001. – 592 с.

 

Для заметок

 

 

Для заметок

 

 

Учебное издание

 

 

МАМОНОВА Татьяна Егоровна