КОНТРОЛЬНЫЕ РАБОТЫ ПО МАТЕМАТИКЕ
Для студентов 1 курса заочного отделения
Специальностей ТПОП и ТЭТ полной и сокращенной форм обучения
Правила выполнения и оформления контрольных работ
Каждое задание контрольных работ содержат 20 вариантов. Номер варианта определятся по номеру, соответствующему списку группы в журнале.
Решение задач необходимо приводить в той же последовательности, в которой представлены контрольные задания. При этом условие задачи должно быть полностью переписано перед ее решением.
Контрольная работа должна быть выполнена в тетради, на обложке которой студент обязан разборчиво написать свою фамилию, инициалы, адрес, шифр, название дисциплины и дату отправления работы в университет.
Если студент испытывает затруднения в усвоении теоретического и практического материала, то он может получить консультацию у преподавателя кафедры.
В прорецензированной зачтенной работе студент должен исправить отмеченные рецензентом ошибки и учесть его рекомендации. Если работа не зачтена, то после исправления ошибок она отправляется на повторную рецензию.
Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.
КОНТРОЛЬНАЯ РАБОТА №1
Линейная алгебра. Аналитическая геометрия. Теория пределов.
| 1. | Дана система линейных уравнений. Требуется: 1) показать, что система совместна; 2) найти ее решение двумя способами: а) по формулам Крамера; б) методом Гаусса; 3) выполнить проверку решения. | ||||
1. 
| 2. 
| ||||
3. 
| 4. 
| ||||
5. 
| 6. 
| ||||
7. 
| 8. 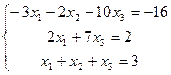
| ||||
9. 
| 10. 
| ||||
11. 
| 12. 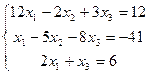
| ||||
13. 
| 14. 
| ||||
15. 
| 16. 
| ||||
17. 
| 18. 
| ||||
19. 
| 20. 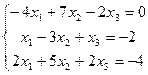
| ||||
| 2. | Методом исключения неизвестных найти общее и базисное решения систем уравнений: | ||||
1. 
| 2. 
| ||||
3. 
| 4. 
| ||||
5. 
| 6. 
| ||||
7. 
| 8. 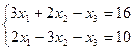
| ||||
9. 
| 10. 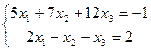
| ||||
11. 
| 12. 
| ||||
13. 
| 14. 
| ||||
15. 
| 16. 
| ||||
17. 
| 18. 
| ||||
19. 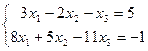
| 20. 
| ||||
| 3. | Даны вершины треугольника 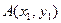 , ,  , ,  . Найти:
а) уравнения всех трех его сторон;
б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;
в) внутренний угол . Найти:
а) уравнения всех трех его сторон;
б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;
в) внутренний угол 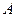 треугольника в градусах и минутах;
г) длину высоты, проведенной из вершины треугольника в градусах и минутах;
г) длину высоты, проведенной из вершины 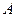 ;
д) площадь треугольника. ;
д) площадь треугольника.
| ||||
1. 
 ,
, 
2. 
 ,
, 
3. 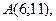
 ,
, 
4. 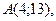
 ,
, 
5. 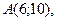
 ,
, 
6. 
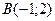 ,
, 
7. 
 ,
, 
8. 
 ,
, 
9. 
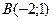 ,
, 
10. 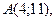
 ,
, 
11. 
 ,
, 
12. 
 ,
, 
13. 
 ,
, 
14. 
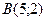 ,
, 
15. 
 ,
, 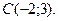
16. 
 ,
, 
17. 
 ,
, 
18. 
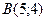 ,
, 
19. 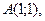
 ,
, 
20. 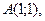
 ,
, 
КОНТРОЛЬНАЯ РАБОТА №2
Дифференциальное и интегральное исчисление.
1. Найти производные  следующих функций: следующих функций:
| |||||||
| 1. | а)  ; ;
| б) 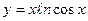 ; ;
| в)  . .
| ||||
| 2. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 3. | а) 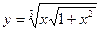 ; ;
| б)  ; ;
| в)  . .
| ||||
| 4. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 5. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 6. | а)  ; ;
| б)  ; ;
| в)  ; ;
| в)  . .
| |||
| 7. | а) 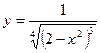 ; ;
| б)  ; ;
| в) 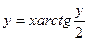 . .
| ||||
| 8. | а)  ; ;
| б) 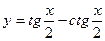 ; ;
| в)  . .
| ||||
| 9. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 10. | а) 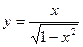 ; ;
| б)  ; ;
| в)  . .
| ||||
| 11. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 12. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 13. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 14. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 15. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 16. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 17. | а) 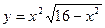 ; ;
| б)  ; ;
| в)  . .
| ||||
| 18. | а)  ; ;
| б) 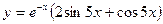 ; ;
| в)  . .
| ||||
| 19. | а)  ; ;
| б)  ; ;
| в) 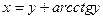 . .
| ||||
| 20. | а)  ; ;
| б)  ; ;
| в)  . .
| ||||
| 2. | Пользуясь правилом Лопиталя найти пределы функций: | ||||
| 1. | а) 
| б) 
| |||
| 2. | а) 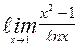
| б) 
| |||
| 3. | а) 
| б) 
| |||
| 4. | а) 
| б) 
| |||
| 5. | а) 
| б) 
| |||
| 6. | а) 
| б) 
| |||
| 7. | а) 
| б) 
| |||
| 8. | а) 
| б) 
| |||
| 9. | а) 
| б) 
| |||
| 10. | а) 
| б) 
| |||
| 11. | а) 
| б) 
| |||
| 12. | а) 
| б) 
| |||
| 13. | а) 
| б) 
| |||
| 14. | а) 
| б) 
| |||
| 15. | а) 
| б) 
| |||
| 16. | а) 
| б) 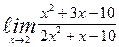
| |||
| 17. | а) 
| б) 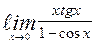
| |||
| 18. | а) 
| б) 
| |||
| 19. | а) 
| б) 
| |||
| 20. | а) 
| б) 
| |||
| 3. | Исследовать функцию и построить ее график | ||||
1.  ; ;
| 2.  ; ;
| 3. 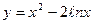 . .
| |||
4. 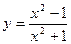 ; ;
| 5.  ; ;
| 6.  . .
| |||
7.  ; ;
| 8.  ; ;
| 9.  . .
| |||
10.  ; ;
| 11.  ; ;
| 12. 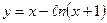 . .
| |||
13.  ; ;
| 14. 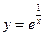 ; ;
| 15.  . .
| |||
16. 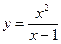 ; ;
| 17.  ; ;
| 18.  . .
| |||
19.  ; ;
| 20.  . .
| ||||
| 4. | Найти частные производные и полный дифференциал функции 
| |
1. 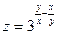 . .
| 2.  . .
| |
3. 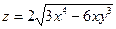 . .
| 4.  . .
| |
5.  . .
| 6.  . .
| |
7.  . .
| 8. 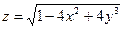 . .
| |
9.  . .
| 10.  . .
| |
11. 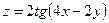 . .
| 12.  . .
| |
13.  . .
| 14. 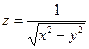 . .
| |
15. 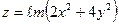 . .
| 16.  . .
| |
17.  . .
| 18.  . .
| |
19.  . .
| 20.  . .
| |
| 5. Найти неопределенные интегралы | |||
| 1. | а)  ; ;
| б)  ; ;
| в) 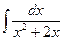 . .
|
| 2. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 3. | а)  ; ;
| б) 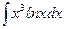 ; ;
| в)  . .
|
| 4. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 5. | а)  ; ;
| б) 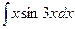 ; ;
| в)  . .
|
| 6. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 7. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 8. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 9. | а)  ; ;
| б)  ; ;
| в) 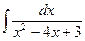 . .
|
| 10. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 11. | а)  ; ;
| б) 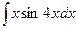 ; ;
| в)  . .
|
| 12. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 13. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 14. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 15. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 16. | а) 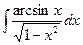 ; ;
| б)  ; ;
| в)  . .
|
| 17. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 18. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 19. | а)  ; ;
| б) 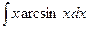 ; ;
| в)  . .
|
| 20. | а)  ; ;
| б)  ; ;
| в)  . .
|
| 6. | Воспользовавшись соответствующим приложением предельного интеграла к задачам геометрии, найти следующее: | |||
| а) площадь фигуры, ограниченную линиями: | ||||
1. y = x2 , y = 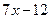 ; ;
| 2. y2 = 2x + 1, x – y – 1= 0; | |||
3. y = x2 , y = 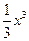 ; ;
| 4. y2 = 9x, y = x + 2; | |||
5.  , y = 1, y = 4; , y = 1, y = 4;
| 6. y = e  , x = 0, x = 2; , x = 0, x = 2;
| |||
7. y = 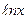 x , x = e-1, x = e; x , x = e-1, x = e;
| 8. y = x2, y =  x3 ; x3 ;
| |||
| 9. y = 2x , x = 0, x = 2; | 10. y = 9 - x2, y = 0. | |||
| б) Объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями. | ||||
11.   , , 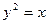
| 12.  , ,  , ,  , , 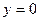 ; ;
| |||
13.   , ,  , , 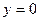
| 14.  , ,  ; ;
| |||
15.   , , 
| 16.  , ,  , , 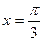 ; ;
| |||
17.  , ,  , ,   ; ;
| 18.  , , 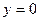 , ,  ; ;
| |||
19.  , , 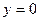 , ,  , , 
| 20. 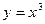 , ,  . .
| |||






