3.1 Оценка (подсчет) итераций.
Если алгоритм содержит итеративную управляющую конструкцию (циклы while или for), то время его работы можно выразить в виде суммы значений времени выполнения отдельных итераций.
При подсчете итераций сумма 
называется арифметической прогрессией и равна 
.
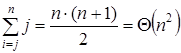Основным способом вычисления сумм рядов является метод математической индукции (от простого – к сложному). Это метод математического доказательства истинности некоторого утверждения (выражения) от натурального аргумента. Например, если утверждение 
истинно, то истинным должно быть и выражение 
для случая 
итераций. Т.е. 
.
3.2 Элементы комбинаторики и работа со строками.
Чтобы ответить на вопрос " сколько? ", не выполняя подсчета, пользуются комбинаторикой.
Например, при построении алгоритмов работы со строками часто преследуют цель поиска некоторой подстроки (подстрок). При этом как правило пользуются формулой вычисления количества размещений с повторениями из 
по 
, где – количество различных символов, из которых состоит строке, а – количество символов подстроки. Под строкой при этом подразумевается символьная последовательность.
Например, если в некоторой строке фигурируют все 33 буквы украинского алфавита, то количество всех возможных подстрок из символов можно вычислить так: 
. Если имеем дело с бинарной строкой, получим выражение 
.
Перестановка. При перестановке элементов строки предполагается, что каждый из символов должен встречаться только 1 раз. Тогда для строки из различных символов имеем 
перестановок.
При перестановке -подстрок справедливо выражение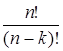 
. Например, для строки 
имеем 6 2-перестановок. Когда порядок следования элементов подстрок не важен, пользуются формулой вычисления сочетаний 
. Так для строки имеем 3 сочетания 2-элементных подстрок.
Например, при работе с текстом часто приходится находить фрагменты, совпадающие с образцом (для осуществления автозамены). Соответствующие алгоритмы работы со строками принято называть алгоритмами сопоставления строк или StringMatching -алгоритмами.
Постановка задачи поиска подстроки по образцу формализуется следующим образом:
– проверяемый текст представим массивом 
, где – длина массива;
– образец (шаблон) – массивом 
, где 
;
– элементами массивов являются символы конечного алфавита 
. Например, 
или 
;
Массивы 
и 
называют строками. также называют подстрокой.
При решении такой задачи говорят, что образец встречается в тексте со сдвигом 
или с позиции 
, если
и 
. (3.1)
При этом как правило преследуют цель найти все возможные сдвиги, для которых бы выполнялось условие (3.1). Если условие выполняется, сдвиги называют корректными или допустимыми. В противном случае – некорректными или недопустимыми.
Существуют различные алгоритмы решения такой задачи: алгоритм Рабина-Карпа, Кнута-Морриса-Пратта и др. Наиболее простой – наивный алгоритм поиска подстрок:
Вычислительная асимптотическая сложность такого алгоритма составляет 
.
3.3 Построение алгоритмов.
Построение алгоритмов производится в соответствии с выбранной стратегией. В качестве примера рассмотрим алгоритм перемножения матриц, руководствуясь стратегией " разделяй и властвуй ", при которой осуществляется декомпозиция (разбиение) задачи на подзадачи.
Пусть имеем две квадратные матрицы размером 
– 
и 
, где 
. Тогда элементы искомой матрицы 
вычисляют по следующей формуле: 
.
Псевдокод алгоритма перемножения матриц представляют следующим образом:
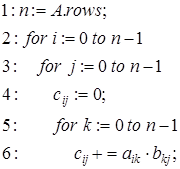
По причине того, что каждый из циклов в тройной вложенности циклов for выполняется ровно раз, а выполнение строки 6 занимает константное время, асимптотическую вычислительную сложность такой реализации можно представить выражением 
.
