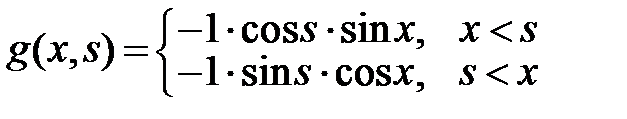In this chapter we consider the Laplace 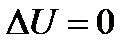 equation in bounded domains
equation in bounded domains  , located on the plane or in space. The points
, located on the plane or in space. The points  and
and 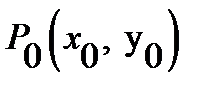 on the plane (or
on the plane (or 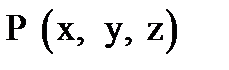 and
and 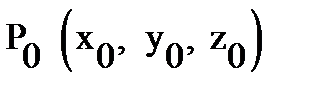 in the space) belong to
in the space) belong to 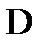 and
and
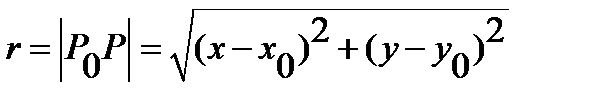 (and
(and
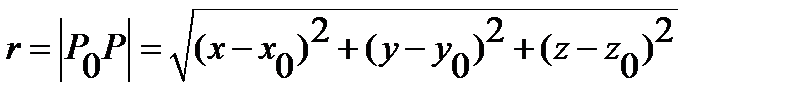 ) - the distance between points
) - the distance between points  and
and  Let us assume that on the boundary of
Let us assume that on the boundary of 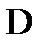 is set to zero Dirichle condition.
is set to zero Dirichle condition.
The function 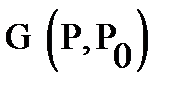 is called the Green's function of the Dirichle problem in the
is called the Green's function of the Dirichle problem in the 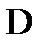 , if for any fixed point
, if for any fixed point 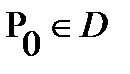 of it, as a function of
of it, as a function of 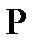 , satisfies the following conditions:
, satisfies the following conditions:
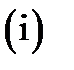 a continuous
a continuous 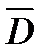 everywhere except at the point
everywhere except at the point 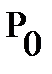 , and
, and 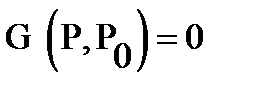 on the boundary of
on the boundary of  ;
;
 a harmonic except at
a harmonic except at  point
point 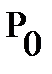 ;
;
 in case the plane is
in case the plane is 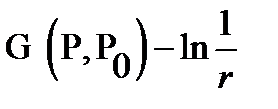 a harmonic function at the point
a harmonic function at the point 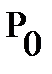 ; if space remains
; if space remains 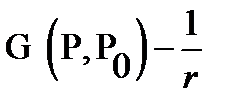 harmonic function at the point
harmonic function at the point 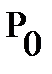 .
.
As follows from the definition of the Green function is continuous and harmonic throughout the domain 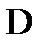 except
except 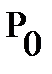 point at which it has a feature type
point at which it has a feature type 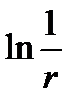 in the plane or
in the plane or 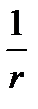 in space. Green's function is sometimes called the source function.
in space. Green's function is sometimes called the source function.
The Green's function 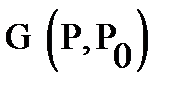 ) (if it exists) is uniquely determined by the properties
) (if it exists) is uniquely determined by the properties 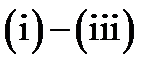 . In addition,
. In addition, 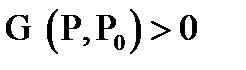 in the domain
in the domain  . Consider, for example, a flat area
. Consider, for example, a flat area  . To prove the uniqueness of the Green's function, we assume the contrary: let
. To prove the uniqueness of the Green's function, we assume the contrary: let 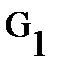 , and
, and 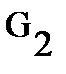 - two functions, possessing properties
- two functions, possessing properties 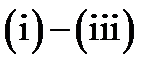 for a given domain
for a given domain  and the point
and the point 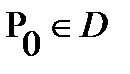 . Then
. Then 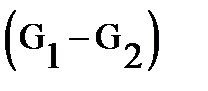 remains harmonic at any point in the area
remains harmonic at any point in the area 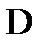 , including point
, including point 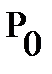 , since the vicinity of the point
, since the vicinity of the point 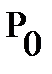 can be written
can be written
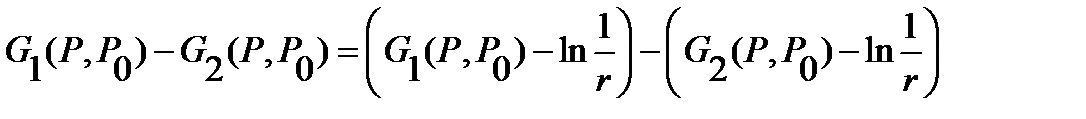
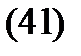
Each bracket on the right side 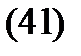 is a function harmonic everywhere in
is a function harmonic everywhere in  (see property
(see property 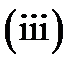 .), And therefore the difference
.), And therefore the difference 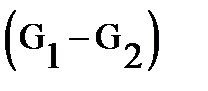 - everywhere in the harmonic function
- everywhere in the harmonic function  . Also, at the boundary function
. Also, at the boundary function 
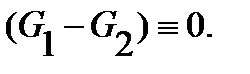 Consequently, by the maximum
Consequently, by the maximum 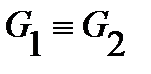 principle in
principle in  .
.
Further, if 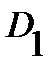 - part of the region
- part of the region 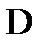 , positioned outside a small neighborhood of the point
, positioned outside a small neighborhood of the point 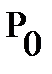 , according to the conditions
, according to the conditions  , the function
, the function 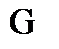 is continuous
is continuous 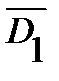 in harmonic
in harmonic 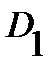 , and on the border
, and on the border 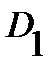 takes non-negative values (as
takes non-negative values (as 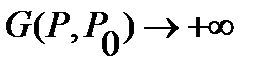 at
at 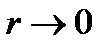 ). Therefore, on the basis of a maximum
). Therefore, on the basis of a maximum 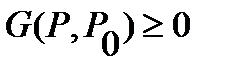 of
of 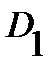 with the zero value inside the area
with the zero value inside the area 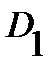 function can not accept. That means that
function can not accept. That means that 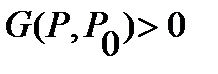 everywhere in
everywhere in  .
.
Example1. In the plane, consider a circle of radius  centered at the origin. We construct the Green's function in the circle. In the construction of this function, we need the concept of conjugate points. Points
centered at the origin. We construct the Green's function in the circle. In the construction of this function, we need the concept of conjugate points. Points 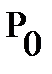 and
and 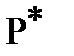 are conjugate with respect to the circle if they lie on the same ray emanating from the center of the circle
are conjugate with respect to the circle if they lie on the same ray emanating from the center of the circle  , and the product of their distances from the center is equal to the square of the radius:
, and the product of their distances from the center is equal to the square of the radius: 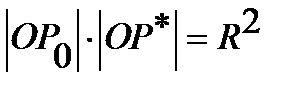 (See Figure16.).
(See Figure16.).
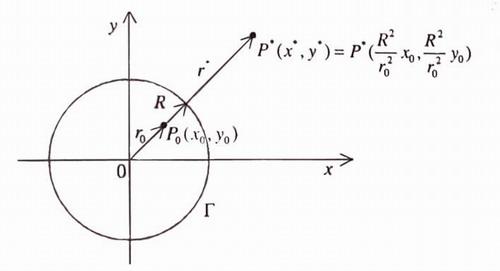
Figure16.
Let 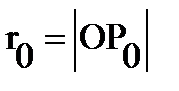 and
and 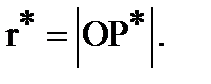 Then
Then 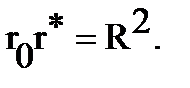 Since the points
Since the points 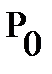 and
and 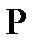 lie on the same ray emanating from the origin, then
lie on the same ray emanating from the origin, then
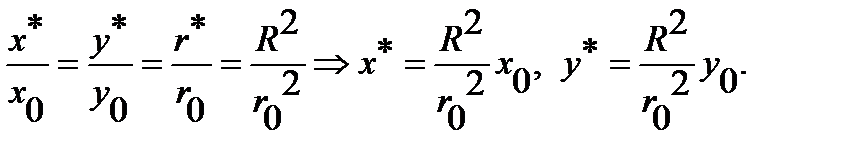
Consider the function
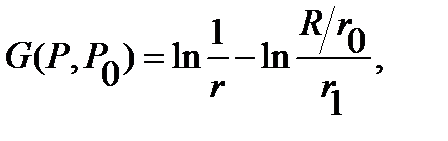
Where  (See. Figure17). We verify that it is the Green's function for the circle.
(See. Figure17). We verify that it is the Green's function for the circle.
By the theorem of cosines  and
and 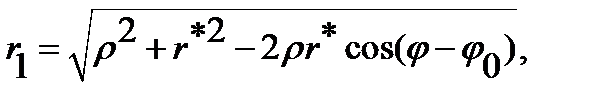 where
where 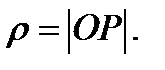
Figure17.
Using the equality 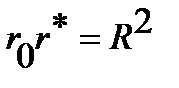 , we obtain
, we obtain 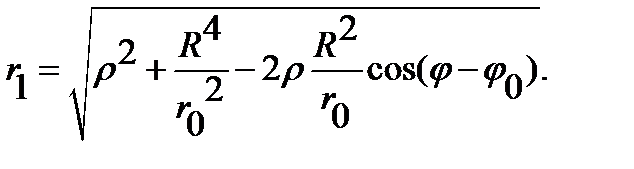 In this way, the value of
In this way, the value of 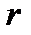 and
and 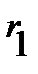 expressed in terms of
expressed in terms of 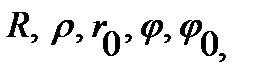 and, ultimately, through
and, ultimately, through 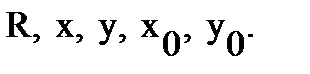 We show that the function
We show that the function 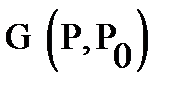 satisfies the items
satisfies the items 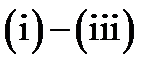 determination. It is obvious that the function is continuous everywhere in the closed circle except at the point
determination. It is obvious that the function is continuous everywhere in the closed circle except at the point 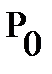 (when
(when 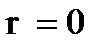 ). At the boundary of a distance
). At the boundary of a distance 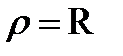 and, hence,
and, hence,
|
|
|
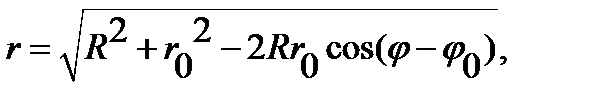
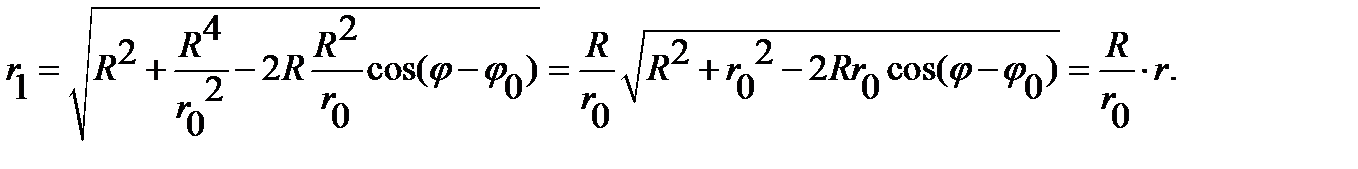
Hence 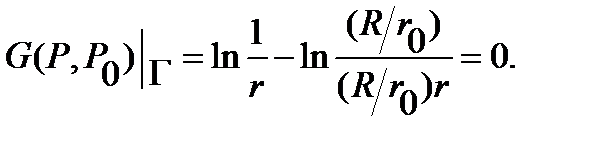 The function
The function 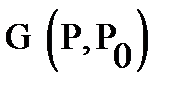 consists of two terms. The first term, the fundamental solution of the Laplace equation and, therefore, harmonic function everywhere except
consists of two terms. The first term, the fundamental solution of the Laplace equation and, therefore, harmonic function everywhere except 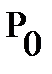 . The function
. The function 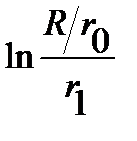 is harmonic throughout the domain
is harmonic throughout the domain 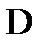 , since the point
, since the point 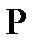 belongs to the region, and the point
belongs to the region, and the point 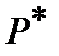 lies outside the region
lies outside the region 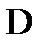 , and hence,
, and hence, 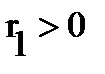 . The harmony of this function is easily verified if we write the Laplace operator in polar coordinates with pole at
. The harmony of this function is easily verified if we write the Laplace operator in polar coordinates with pole at 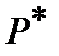 (sm. A similar formula
(sm. A similar formula 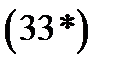 with a pole at the point
with a pole at the point  ):
):
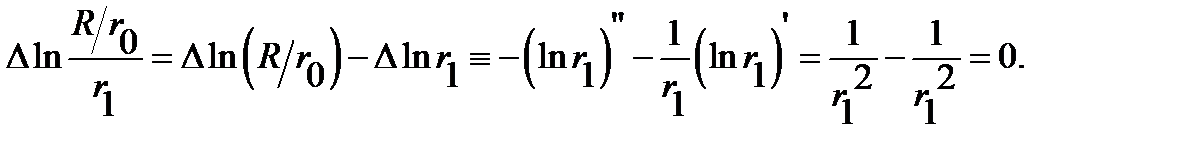
Therefore, the function 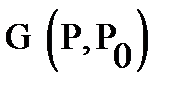 in
in 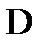 harmonic everywhere except at the point Po, and the difference
harmonic everywhere except at the point Po, and the difference 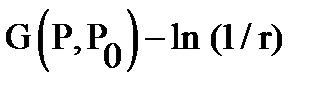 ) - harmonic and at the point
) - harmonic and at the point 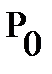 .
.
Similarly, construction of Green's function for a sphere of radius 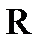 . It has the form
. It has the form 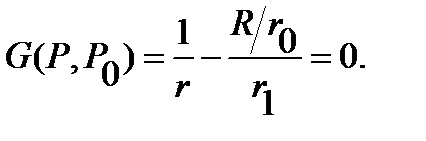 Where
Where 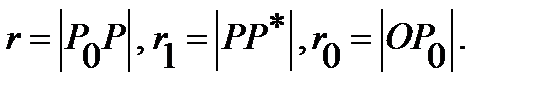 Point
Point 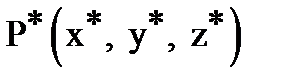 conjugate point
conjugate point 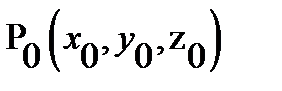 with respect to a sphere of radius
with respect to a sphere of radius 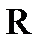 centered at
centered at  , that is
, that is 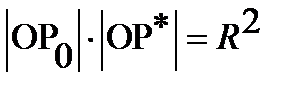 . The coordinates
. The coordinates 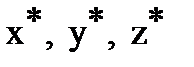 are calculated according to the formulas:
are calculated according to the formulas:
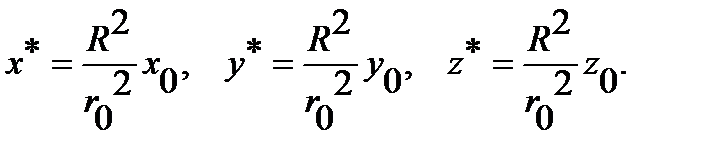
Example2. Green's function can be viewed not only limited, but also for unbounded domains. As an example, we construct the Green's function for the half-plane. To do this, we define a point conjugate with respect to the line: points  and
and  are conjugate with respect to a straight line, if they are symmetrical with respect to this line (see. Figure18).
are conjugate with respect to a straight line, if they are symmetrical with respect to this line (see. Figure18).
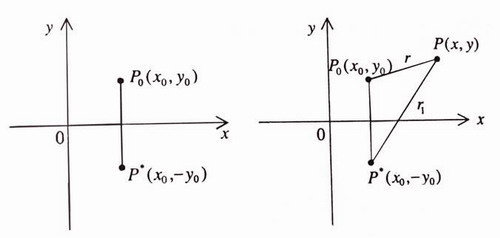
Figure18. Figure19.
The function 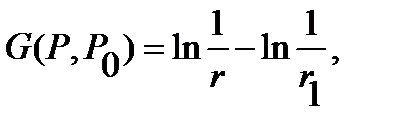 where
where
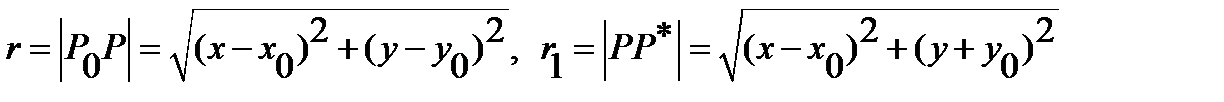
(See Figure19.), satisfies the properties 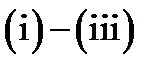 in the half-plane
in the half-plane 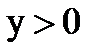 . In fact, on the boundary at
. In fact, on the boundary at 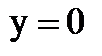 distance
distance 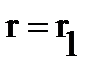 , so
, so 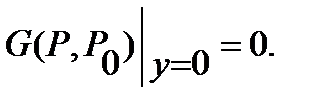 The harmony function
The harmony function  everywhere in the region
everywhere in the region 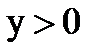 can be verified directly by calculating the partial derivatives:
can be verified directly by calculating the partial derivatives:
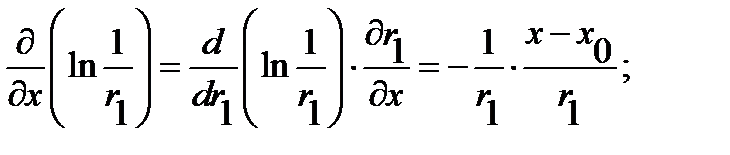
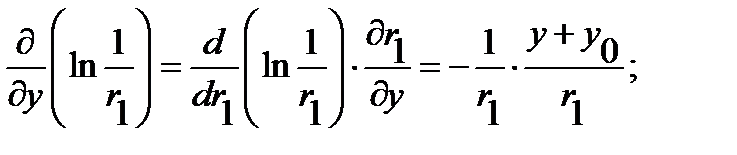
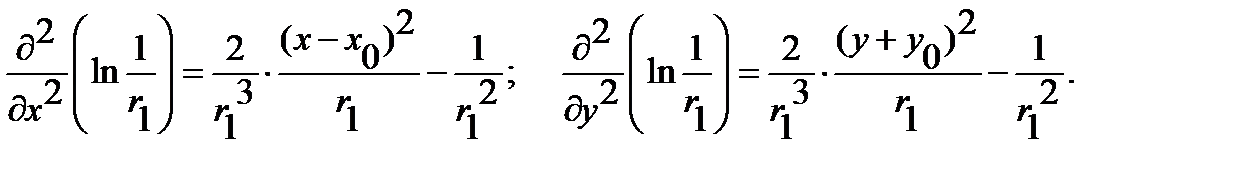
So
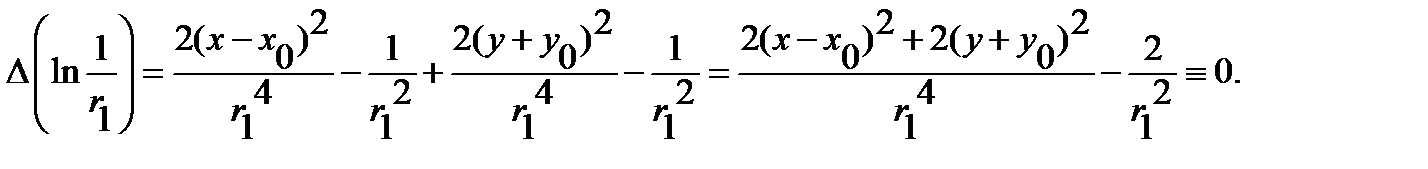
Consequently, the function 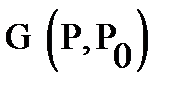 harmonic in the domain
harmonic in the domain 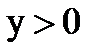 everywhere except at the point
everywhere except at the point 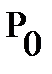 , and the difference
, and the difference 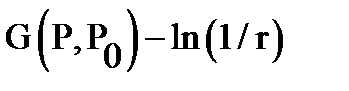 and the harmonic at the point
and the harmonic at the point 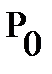 .
.
For the half 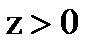 and the Green's function has the form
and the Green's function has the form
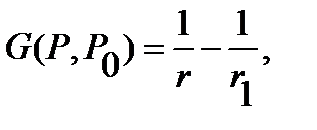
Where 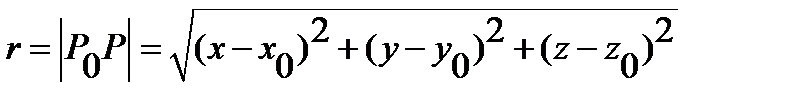
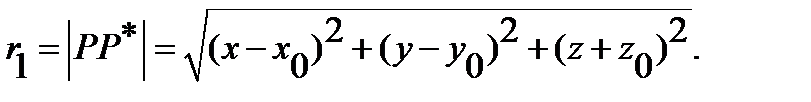
Examples:
Given the problem
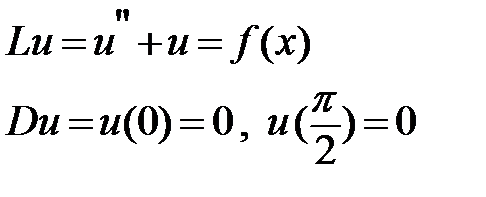
Find Green's function.
First step: From demand-2 we see that
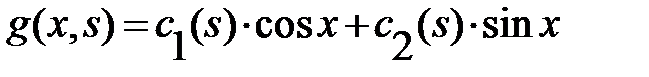
For 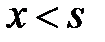 we see from demand-3 that the
we see from demand-3 that the 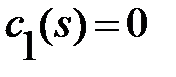 , while for
, while for 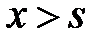 we see from demand-3 that the
we see from demand-3 that the 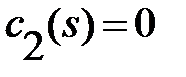 (we leave it to the reader to fill in the in-between steps).
(we leave it to the reader to fill in the in-between steps).
Summarize the results:
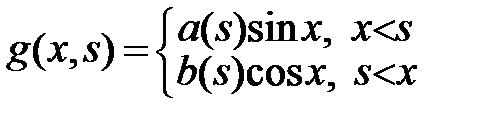
Second step: Now we shall determine 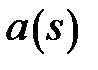 and
and 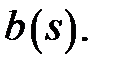
Using demand-1 we get
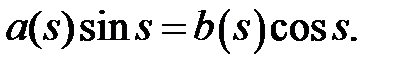
Using demand- 4 we get
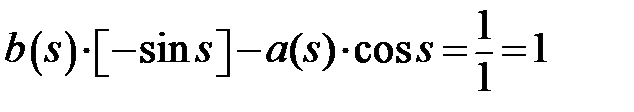
| |
Using Cramer's rule or by intelligent guess solve for 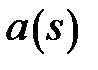 and
and 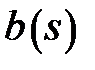 and obtain that
and obtain that
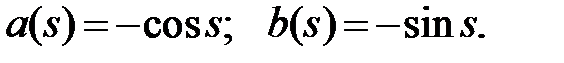
Check that this automatically satisfies demand-5.
So our Green's function for this problem is: