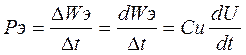ЛЕКЦИЯ 7
Установившиеся режимы в цепях несинусоидального тока
Представление периодических несинусоидальных сигналов
Помимо синусоидальных токов и напряжений в электронике широко используются несинусоидальные периодические токи и напряжения.
Например, выпрямители имеют одно и двухполупериодные мгновенные значения токов и напряжений.
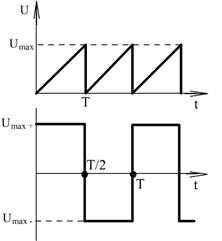
Или ГЛИН (генераторы линейно изменяющихся напряжений) и мультивибратор на выходе имеют пилообразное напряжение или U – прямоугольной формы.
Периодические несинусоидальные функции времени f(t) при любых t должны удовлетворять условию:
, где Т – период колебаний.
Наглядным способом представления несинусоидальных величин являются кривые и их мгновенные значения, которые можно наблюдать на осциллографе.
Второй способ это представление этих функций в тригонометрический ряд Фурье.
Тригонометрический ряд Фурье быстро сходится, поэтому для инженерных расчетов количество гармоник ограничивают 3-5 членами ряда.
Например, напряжение в нагрузочном резисторе однополупериодного выпрямителя.
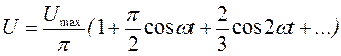
Напряжение пилообразной формы:
Напряжение прямоугольной формы:
Гармоника это, когда несинусоидальную функцию можно разложить на простейшие синусоидальные функции, отличающиеся амплитудой, частотой и фазой.
Действующие и средние значения несинусоидальных величин
Несинусоидальную функцию характеризуют следующими параметрами:
максимальным значением Im
действующим значением I
средним по модулю значением Iср
и постоянной составляющей Iо
Действующее значение несинусоидальной электрической величины (определяется его среднеквадратичное значение за период) равно корню квадратному из суммы квадратов постоянной составляющей и действительных значений всех гармоник.
Действительное: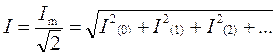 
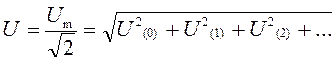
Среднее по модулю:
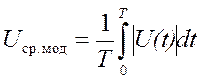
Постоянная составляющая:
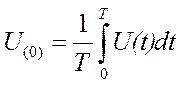
Коэффициенты, характеризующие несинусоидальные сигналы
Коэффициенты амплитуды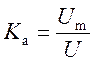 
, для синусоидального K a = 
, чем острее кривая, тем больше К а.
Коэффициенты формы 
, для синусоидальных величин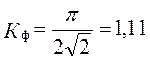 
Коэффициент искажений К И = U 1/ U
Коэффициент гармоник К Г = U г/ U
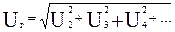
действующее значение высших гармоник
Коэффициент несинусоидальности Кп
Коэффициент пульсации p – определяется отношением амплитуды первой (основной) гармоники к постоянной составляющей
Этим коэффициентом пользуются для оценки содержания переменной составляющей в кривых напряжений и токов выпрямителей.
Задача
| ¡ E = U o + U m·sin(ωt + 45), U o = 45 B, U = 39 B, ¡ R 1= R 2 =50 Ом, L = 0,127 Гн, C = 3,18 мкФ ¡ Определить U c, I 2 |
Решение
по постоянной составляющей
Е 1 = U o = 45 B
I 2 = U o/ R 1 = 0,9 A I 3 = 0
По переменной составляющей X L= 40, Ом X c = 1000 Ом
е = U √2·sin(ωt + 45о)
е = 39√2·sin(314t + 45о)=55·sin(314t + 45о)
 | |||
 |
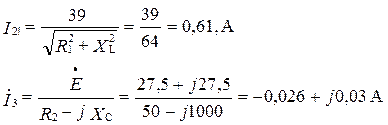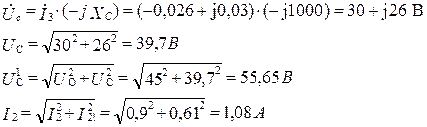Переходные процессы в электрических цепях
Понятие о переходных процессах. Условия возникновения переходных процессов.
Электромагнитные процессы, возникающие в электрической цепи, при переходе от одного установившегося режима к другому, называются переходными.
Переходные процессы вызываются изменением параметров схемы, чаще всего в результате коммутации в цепи.
Коммутацией (переключением) называется процесс замыкания и размыкания выключателей.
Физически возникновение переходных процессов объясняется тем, что изменение энергии электромагнитных полей не может происходить мгновенно (скачком) в таких элементах как конденсатор и катушка индуктивности, т.к. это инерционные элементы.
Время переходного процесса много меньше сотых долей секунды.
Уравнения для решения переходных процессов.
i пер = i уст + i св
U пер = U уст + U св
i y и U y находят для установившегося процесса, т.е. когда переходный процесс закончен.
i св и U св – находятся когда в цепи нет источника энергии, т.е. i и U определяются только параметрами элементов цепи.
Решение уравнений осуществляется на основании двух законов коммутации.
Первый закон коммутации
Ток в ветви с индуктивной катушкой не может измениться скачком. В первый момент переходный ток сохраняет значение, которое он имел в момент, предшествующий коммутации, т.е. i(0-) = i(0+).
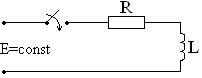I = 0 ÷ E / R
в t (0-) → I = 0
в t (∞) → I = E / R
Этот вывод сделан на основании невозможности мгновенного изменения электрической и магнитной энергии.
Т.е. пусть ток в катушке индуктивности изменяется скачком, тогда: 
и запасенная энергия тоже должна изменяться скачками.
Т.к. 
, то 
и 
Но мощность не может быть бесконечно большой, поэтому ток в катушке изменяться скачком не может в отличие от напряжения.
Второй закон коммутации
Напряжение на конденсаторе не может изменяться скачком, т.е. U (0-) = U (0+)
Рассмотрим цепь RC
Уравнение по второму закону Кирхгофа:
E = iR + Uc
t (0-) → U c(0-) = 0
t → ∞ U c = E
Доказательство:
Допустим, что U c изменилось скачком, тогда 
поэтому бесконечно большой электрической мощности быть не может
