Рекурсивные звенья 1-го и 2-го порядков
Рекурсивными звеньями 1-го и 2-го порядков (коротко звеньями) называют рекурсивные ЛДС 1-го и 2-го порядков:
1) передаточная функция звена 1-го порядка:
; (4.7)
2) передаточная функция звена 2-го порядка (биквадратного звена):
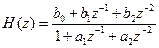. (4.8)
Звено называют базовым, если числитель его ПФ равен единице:
1) передаточная функция базового звена 1-го порядка:
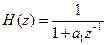; (4.9)
2) передаточная функция базового звена 2-го порядка:
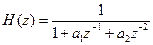. (4.10)
В таблице соответствий имеем соответствие между
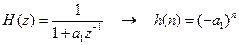; (4.11)
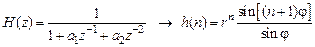. (4.12)
4.3. Нули и полюсы ПФ. Карта нулей и полюсов
Нулями передаточной функции (4.5) называют значения z, при которых
Полюсы передаточной функции (4.5) называют значения z, при которых
Карта нулей и полюсов — это изображение нулей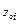 
(кружками) и полюсов 
(звездочками) на z -плоскости одновременно с единичной окружностью.
Для определения нулей и полюсов дробно-рациональной передаточной функции следует ее представить в виде отношения многочленов— выразить относительно положительных степеней z!
Пример 4.1 (самостоятельно)
Определить нули и комплексно-сопряженные полюсы передаточной функции звена 2-го порядка:
(4.13)
и построить карту нулей и полюсов (см. аналогично в примере 3.8):
1. Записываем соответствие между передаточной функцией и ИХ для базового звена 2-го порядка:
2. Определяем радиус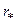 
и аргумент 
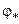комплексно-сопряженных полюсов:
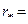
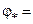
3. Записываем комплексно сопряженные полюсы:
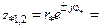
4. Для определения нулей выражает передаточную функцию относительно положительных степеней z:
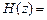
5. Записываем нули:
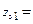
6. Если нули оказались комплексно-сопряженными, определяем их радиус 
и аргумент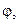 
:
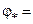
и записываем нули в виде:
7. Строится карта нулей и полюсов.
4.4. Взаимосвязь передаточной функции и разностного уравнения
Взаимосвязь передаточной функции и РУ следует из их сравнения:
.
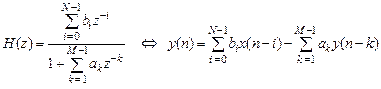Выводы:
1. Числитель передаточной функции соответствует
Знак коэффициентов 
Степень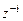 
соответствует
2. Знаменатель передаточной функции соответствует
Единица соответствует
Знак коэффициентов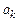 
Степень 
соответствует
Пример 4.2
Записать РУ звеньев 1-го и 2-го порядков по их передаточным функциям:
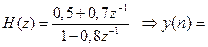
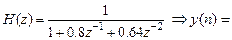
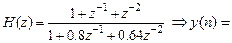
Пример 4.3
Записать передаточную функцию, соответствующую РУ:
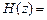
4.5. Разновидности представления ПФ
Разновидности представления рекурсивных ЛДС обусловлены различным математическим представлением дробно-рациональной функции (4.5):
:
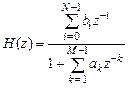1) произведение простейших множителей:
,
где 
— нули и полюсы, в общем случае – комплексно сопряженные;
2) произведения множителей второго порядка с вещественными коэффициентами:
,
или при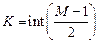 
:
; (4.14)
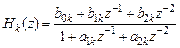; (4.15)
3) сумма простых дробей:
, (4.16)
где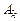 
—
4) сумма дробей второго порядка с вещественными коэффициентами:
;
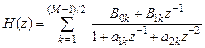или при :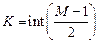
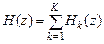, (4.17)
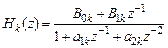. (4.18)
Второй критерий устойчивости ЛДС
Определим отображение в z-области первого критерия устойчивости (2.7):
. (2.7)
Представим передаточную функцию в виде суммы простых дробей:
.
Определим ИХ:
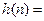
и подставим в (2.7):
Второй критерий: необходимым и достаточным условием устойчивости ЛДС является
