Характеристики ступени турбины

Обсуждено на заседании ПМК

«____»_______________2010 г.

протокол № ___

г. Москва

УЧЕБНЫЕ И ВОСПИТАТЕЛЬНЫЕ ЦЕЛИ:

1. Изложить (подробно) форму представления и характер протекания характеристик ступени турбины.

2. Рассмотреть особенности протекания характеристик многоступенчатых турбин.

Время: 2 часа

ПЛАН ЛЕКЦИИ:

УЧЕБНО-МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ:

Наглядные пособия __плакаты по рис. 8.3, 8.4 и рис. 8.5 из учебника.

ЛИТЕРАТУРА:

1. Нечаев Ю.Н., Федоров Р.М., Котовский В.Н., Полев А.С. Теория авиационных двигателей, часть 1. ВВИА, 2006г., стр. 205-215.

ХАРАКТЕРИСТИКИ СТУПЕНИ ТУРБИНЫ

Характеристики ступени турбины могут представляться в той же форме, что и характеристики турбины в целом, только с заменой индекса “г” (сечение на входе) на индекс “0” и ин­декса “т” (сечение на выходе)на индекс “2”).

На расчетном режиме работы, как уже отмечалось, степень понижения давления в каждой ступени турбины может достигать значений 2…3 и более. Соответственно при типичных значениях степени реактивности степень понижения давления в сопловом аппарате ступени близка к критической или превышает её.. Поэтому при увеличении (по сравнению с расчетной) общей степени понижения давления в ступени значение в горле межлопаточного канала соплового аппарата и соответственно на входе в него не возрастает или почти не возрастает (как в суживающемся сопле). Но тогда так же не изменяется или почти не изменяется и параметр расхода , пропорциональный . Расчеты и опыт показывают, что и степень понижения давления газа в сопловом аппарате в этом случае тоже не возрастает или возрастает гораздо медленнее, чем в рабочем колесе. При снижении (по сравнению с расчетной) общей степени понижения давления в ступени наблюдается аналогичная картина: степень понижения давления в РК уменьшается быстро, а в СА значительно медленнее. Параметр расхода уменьшается ещё медленнее. И только при весьма существенном снижении общей степени понижения давления в ступени (практически выходящем за область эксплуатационных режимов работы турбины в системе ГТД) степень понижения давления в СА и параметр расхода газа начинают быстро падать. Это необходимо учитывать только, например, при детальных расчетах процесса запуска авиационных ГТД.

Рис. 8.1. Характеристика ступени турбины при

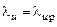
Рассмотрим сначала влияние степени понижения давления газа на параметры ступени при расчетном значении (или ), показанное (качественно) на рис. 8.1. Вначале рассмотрим влияние 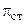и соответственно . По мере возрастания степени пони­жения давления газа в ступени (начиная со значений, близких к 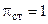) растет соответственно и перепад давлений на сопловом аппарате. Увеличение вызывает уве­личение скорости истечения газа из соплового аппарата и соответственно рост скорости на входе в него, т.е. . Следовательно, увеличивается и параметр , пропорциональный . 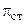(При малых значениях этот параметр возрастает сначала почти пропорционально величине 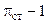). Однако увеличение будет продолжаться лишь до тех пор, пока степень понижения давления газа в сопловом аппарате не станет близкой к её критическому значению (произойдет “запирание” СА) или пока не будет до­стигнута скорость звука в межлопаточных каналах находящегося за ним рабочего колеса (“запирание ” РК). При этом при пониженных значениях 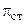, как показывают опыт и расчеты, “запирание” СА обычно происходит раньше, чем «запирание» РК. Дальнейшее увели­чение уже не будет оказывать влияния на параметр расхода. Аналогично влияет на параметр расхода газа и 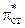(см. рис. 8.1).

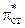Рассмотрим далее изменение КПД ступени при изменении . Его можно объяснить, используя рассмотренное нами ранее влияние на КПД параметра При расчетных значениях и 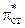величина близка к оптимальной и соответственно имеет значение, близкое к максимальному. Малым 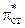(и соответственно малым с ₁) при расчетном значении соответствует значение , существенно превышающее расчетное. Поэтому с ростом (начиная с ) значение уменьшается, в результате чего сперва растет, достигает максимума (при значении 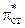, близком к расчетному), а затем снижается, как показано верхней кривой на рис. 8.1. Аналогично изменяется и .

Если бы значение при изменении оставалось неизменным, то параметр работы ступени 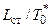в соответствии с формулой (8.4) изменялся бы в зависимости от так, как показано на рис. 8.1 штриховой линией. Но с учетом изменения эта зависимость протекает так, как показано на рис. 8.1 сплошной линией.

Отметим еще одну важную деталь характеристики ступени турбины. При анализе характеристики компрессора уже наблюдалось «запирание» его выходного направляющего аппарата. Аналогичное явление имеет место и в турбинах, но со следующими особенностями.

Если степень понижения давления в сопловом аппарате превышает критическое значение 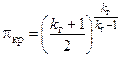, то в минимальном сечении межлопаточного канала решетки СА скорость газового потока достигает скорости звука, а за этим сечением продолжается расширение газа и увеличение его скорости в так называемом косом срезе межлопаточного канала. Это происходит следующим образом (рис. 8.2). За минимальным сечением m-m¢ около выходной кромки (в точке т') происходит поч­ти скачкообразное падение давления от давления в этом сечении до давления за решеткой. В результате этого из точки т' исходит серия волн разрежения, при прохождении через которые поток газа разгоняется и одновременно поворачивается в сторону увеличения угла 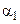. Так достигается сверхзвуковая скорость в решетке, составленной из сужающихся каналов, но имеющей угол выхода потока, существенно отличный от 90^о.

Отражение волн разрежения от спинки соседней лопатки и возникновение скачков уплотнения в результате взаимодействия струй, вытекающих из соседних кана­лов, делает общую картину течения газа более сложной, но не из­меняет основной ее особенности, за­ключающейся в возможности достиже­ния сверхзвуковой скорости газа в ко­сом срезе. Однако этот процесс может продолжаться лишь до тех пор, пока волны разрежения, выходящие из точки m¢, попадают на спинку соседнего профиля, т.е. до тех пор, пока последняя из них не станет практически параллельной фронту решетки. Можно показать, что при этом осевая составляющая скорости газа на выходе из решетки становится равной скорости звука.

Аналогичная картина наблюдается в решетке рабочего колеса турбинной ступени, если степень понижения давления газа в ней, определенная как отношение полного давления газового потока (в относительном движении) на входе в нее к статическому давлению на выходе, становится больше критической. В этом случае (при данном значении ) дальнейшее увеличение 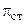уже не сказывается на структуре течения газа до рабочего колеса, но величина работы на валу ступени продолжает увеличиваться за счет расширения газа в косом срезе решетки рабочего колеса до тех пор, пока осевая составляющая скорости газа за РК не станет равна скорости звука. Дальнейшее увеличение 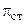(и ) становится невозможным.

Таким образом, максимальное значение степени понижения давления в ступени турбины ограничено условием достижения осевой составляющей скорости газа за РК, равной скорости звука. Этот режим отмечен на рис. 8.1 штриховкой справа.

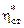Рис. 8.3. Характеристика ступени тазовой турбины: а) – изменение и ; б) – изменение и ; кривые 1 – при ; кривые 2 – при ; кривые 3 – при

При изменении значения (или параметра ) по сравнению с расчетным значением все кривые, изображенные на рис. 8.1, несколько смещаются и деформируются.

На рис. 8.3 приведен пример характеристики ступени с 2,2 при различных значениях 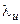. При расчетном значении 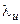кривые , и (кривые 1 на рис.8.3) протекают в зависимости от примерно так же, как и на рис. 8.1. При снижени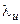и (или ) по сравнению с его расчетным значением для сохранения близкого к оптимальному значения необходимо снижать и . Поэтому максимум достигается в этом случае при меньшем значении . Соответственно деформируется и зависимость от .

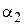На рис8.3 приведены также значения угла на выходе из ступени в зависимости от и . Как видно, изменение параметра 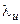в указанном на рис. 8.3 диапазоне сравнительно слабо влияет на параметры расхода газа и работы ступени турбины, но заметно сказывается на значении угла .