Лекция 11. Дискретные сигналы
1. Описание дискретных сигналов в z -области.
2. Описание дискретных сигналов в частотной области.
3. Основные свойства спектральной плотности.
4. Связь спектральных плотностей дискретного и аналогового сигналов.
5. Операции со спектральной плотностью:
· сдвиг;
· инверсия;
· формирование сигнала с ОБП.
11.1. Описание дискретных сигналов в z -области
В z-области дискретный сигнал описывается своим …
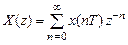 . (11.1)
. (11.1)
Описание дискретных сигналов в частотной области
В частотной области дискретный сигнал описывается своим …
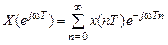 , (11.2)
, (11.2)
называемым спектральной плотностью (СП).
В шкале дискретного нормированного времени и нормированной частоты:
 . (11.3)
. (11.3)
Спектральная плотность связанна с z -изображением соотношением:
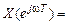 (11.4)
(11.4)
11.3. Основные свойства спектральной плотности:
1. СП 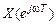 – непрерывная функция частоты.
– непрерывная функция частоты.
2. СП  – периодическая функция частоты с периодом в шкалах частот
– периодическая функция частоты с периодом в шкалах частот 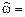 ,
,  и
и 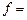 .
.
Доказательство:
3. Свойство линейности СП:
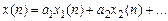
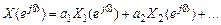
Доказательство следует из …
4. Для вещественного дискретного сигнала модуль СП – четная, а аргумент –нечетная функция частоты.
Доказательство.
5. Модуль (и аргумент) СП вещественного дискретного сигнала рассматривают в основной полосе частот 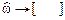 , а комплексного – на периоде
, а комплексного – на периоде 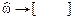 .
.
Запишите соответствие в шкалах  и
и  :
:
Поясните, почему это так для модуля СП.
6. Равенство Парсеваля (пояснить смысл, обратить внимание на пределы суммирования):
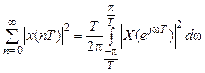 . (11.5)
. (11.5)
В (11.5) устанавливается равенство между…
Пределы интегрирования в (11.5) не бесконечные, т.к. СП рассматривается на интервале …
7. Сдвиг СП:
Сдвиг СП вправо реализуется умножением исходной последовательности на экспоненту  :
:
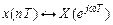 ;
;
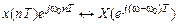 . (11.6)
. (11.6)
Доказательство:
Сдвиг СП влево реализуется умножением исходной последовательности на экспоненту…
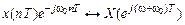 . (11.7)
. (11.7)
8. Сдвиг (задержка) дискретного сигнала:
Дискретному сигналу, задержанному на m отчетов, соответствует умножение СП на экспоненту  , т. е. к изменению… СП:
, т. е. к изменению… СП:
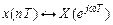
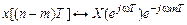 . (11.8)
. (11.8)
Доказательство:
Связь спектральных плотностей дискретного и аналогового сигналов
Если дискретный сигнал 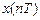 получен в результате дискретизации аналогового сигнала
получен в результате дискретизации аналогового сигнала  , то связь между их СП-ми будет иметь вид:
, то связь между их СП-ми будет иметь вид:
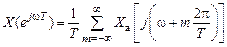 . (11.9)
. (11.9)
Спектральная плотность дискретного сигнала равна…
Связь (11.9) иллюстрируется на рис. 11.1.
Выводы:
1. Точное восстановление аналогового сигнала возможно при 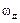
2. При 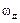 наблюдается …
наблюдается …
Рис. 11.1 иллюстрирует теорему…

Рис. 11.1. Связь СП дискретного и аналоговых сигналов: модуль финитная СП финитного сигнала (а); модуль СП дискретного сигнала при: 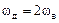 (б);
(б); 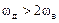 (в);
(в);  (г)
(г)
Операции со спектральной плотностью
Сдвиг СП – см. свойство 6.
Инверсия СП вещественного сигнала (рис. 11.2)
В результате инверсии любая спектральная составляющая 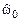 модуля СП оказывается на противоположной частоте:
модуля СП оказывается на противоположной частоте:
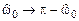 .
.
При инверсии СП вещественного сигнала должны обеспечить:
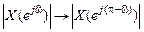 . (11.10)
. (11.10)
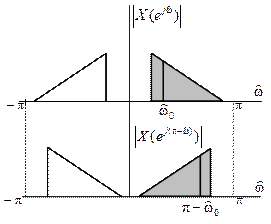
Рис. 11.2. Инверсия СП
Инверсную СП можно получить посредством…
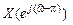
Инверсная СП:
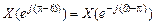
Модули СП 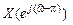 и
и  вещественного сигнала …, а аргументы…, т.к.
вещественного сигнала …, а аргументы…, т.к.
Сдвиг СП вправо реализуется посредством…

т.е.
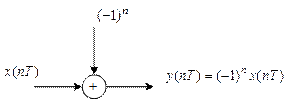
Рис. 11.3. Алгоритм реализации инверсии СП
Формирование сигнала с ОБП (рис. 11.4)

Рис. 11.4. Формирование сигнала с ОБП
Последовательность действий (алгоритм) формирования сигнала с ОБП
На рис. 11.4, а – СП вещественного сигнала с двумя БП. Будем выделять правую полосу.
1. Сдвиг СП влево на частоту  – рис. 11.4, а:
– рис. 11.4, а:
 . (11.11)
. (11.11)
Реализация сдвига влево (рис. 11.5):
 .
.
2. Фильтрация комплексного сигнала 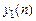 с помощью комплексного ФНЧ (КФНЧ).
с помощью комплексного ФНЧ (КФНЧ).
КФНЧ представляет собой…
На рис. 11.4, в представлено условное изображение АЧХ КФНЧ.
На рис. 11.4, г – СП 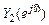 на выходе КФНЧ
на выходе КФНЧ
На рис. 11.5 – … сигнал 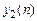 на выходе КФНЧ.
на выходе КФНЧ.
3. Сдвиг СП 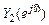 на частоту
на частоту  вправо – рис. 11.4, д.
вправо – рис. 11.4, д.
Реализация сдвига вправо (рис. 11.5):
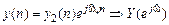 .
.
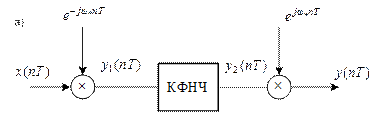
Рис. 11.5. Алгоритм формирования сигнала с ОБП






