Упорядкований рух електричних зарядів називається електричним струмом.
Сила струму. Середня сила струму за час Δt
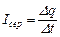, (4.1)
де Δq – заряд, що проходить через поперечний переріз провідника за час Δt.
Миттєве значення сили струму:
, (4.2)
тобто миттєва сила струму дорівнює першій похідній від заряду за часом. За напрямок струму приймається напрямок переміщення позитивних зарядів.
Якщо в провіднику рухаються заряди обох знаків, то сила струму:
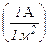. (4.3)
Густина струму. При нерівномірному розподілу по поперечному перерізу провідника зарядів, що проходять по ньому, струм характеризується густиною струму:
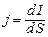, (4.4)
де dS – елементарна площадка, перпендикулярна напрямку протікання струму. Знаючи густину струму j, можна визначити силу струму
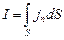, (4.5)
де jn = j cosα – проекція вектора густини струму на нормаль до поверхні S у кожній точці поверхні.
Електрорушійна сила джерела (EPC) струму. Сили електричного поля переміщують позитивні заряди від точок з більшим потенціалом до точок з меншим потенціалом.
У замкненому колі поряд з ділянками зі зменшенням потенціалу мають бути ділянки із зростанням потенціалу. На ділянках із зростанням потенціалу переміщення позитивних зарядів можливе за допомогою тільки неелектричних (сторонніх) сил.
Сила будь-якої природи, яка може переміщувати позитивний заряд у напрямку зростання потенціалу, відноситься до класу сторонніх сил. Сторонні сили можна характеризувати роботою з переміщення одиничного позитивного заряду. Ця величина називається електрорушійною силою і дорівнює
E = Aст /q (1Дж/кл = 1 В). (4.6)
Сторонні сили діють у джерелах струму і переміщують позитивні заряди від меншого потенціалу (від мінусу) до більшого (до плюсу). Саме джерело струму витрачає енергію на переміщення зарядів по замкненому колу, тому що робота електричних сил, які переміщують заряд поза джерелом, по замкненому колу дорівнює нулю.
Напруга. Розглянемо ділянку кола, яка має джерело струму. (див. рис. 42).
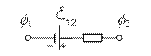Рис.42
Повна робота А12 з переміщення заряду q по ділянці кола складається з роботи сторонніх сил у джерелі струму і роботи електричних сил поза джерелом струму
A12 =A12ел +A12ст. (4.7)
Поділимо формулу (4.7) на заряд q, що переміщується по ділянці, і введемо такі величини: U12= A12 /q – напруга на ділянці кола, j1 – j2 = A12ел /q 
– різниця потенціалів на ділянці кола, E12= A12ст /q – EPC ділянки кола. У результаті формулу (4.7) можна переписати у вигляді
U12= (j1 – j2) + E12 .
Таким чином, напруга на ділянці кола дорівнює алгебраїчній сумі різниці потенціалів і EPC. Якщо напрямок дії джерела струму (від мінуса до плюса) збігається з напрямком струму, то Е12 > 0, а якщо не збігається, то Е12 < 0.
Закон Ома для ділянки кола. Сила струму на ділянці кола прямо пропорційна напрузі і обернено пропорційна електричному опору ділянки кола
. (4.8)
Для циліндричних провідників електричний опір визначається формулою
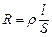, (4.9)
де ρ – питомий опір провідника, l – довжина, S – площа поперечного перерізу провідника.
Закон Ома можна записати у диференціальній формі:
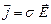, (4.10)
де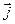 
– вектор густини струму, 
– напруженість електричного поля в провіднику, s=1/r – електропровідність провідника. Закон Ома у вигляді (4.10) дозволяє диференційно підійти до різних ділянок поперечного перерізу провідника і відповісти на питання, як змінюється густина струму по поперечному перерізу провідника. З формули (4.10) випливає, що розподіл густини струму збігається з розподілом напруженості електричного поля на поперечному перерізі провідника.
Питомий опір більшості металевих провідників залежить від температури за формулою
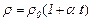, (4.11)
де ρ0 – питомий опір за температури t = 0o C, α – температурний коефіцієнт опору. При кімнатних температурах ρ змінюється прямо пропорційно абсолютній температурі Т = t oC + 273. Однак при низьких температурах спостерігається відхилення від цієї залежності (див. рис. 43).
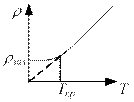
Рис. 43
При Т =0 спостерігається залишковий опір ρзал , який залежить від чистоти матеріалу і наявності механічних напружень. У деяких матеріалів та сплавів при Т < Ткр (тобто при температурі нижче критичної) спостерігається падіння електричного опору до нуля.
Це явище називається надпровідністю. Надпровідниками є ртуть, олово, свинець, алюміній та інші.
Температура, при якій провідник переходить у стан надпровідності, називається критичною і є дуже малою (кілька Кельвінів).
Закон Джоуля. При протіканні струму по провіднику останній нагрівається, тобто виділяється теплота. Ця теплота називається джоулевою теплотою оскільки, визначається за законом Джоуля. Для постійного струму закон Джоуля
,
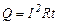де I – сила постійного струму, R – опір провідника, t – час протікання струму.
Для змінного струму весь час протікання струму потрібно розбити на елементарні проміжки часу Δtk, настільки малі, що струм Ik на кожному з них, можна вважати незмінною величиною, тоді
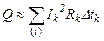, (4.12)
Формула (4.12) тим точніша, чим менші проміжки часу Δtk. Строгий знак рівності можна підставити тільки під знаком границі
, (4.13)
Тобто щоб визначити кількість теплоти, що виділяється при протіканні змінного струму, потрібно вираз I2R проінтегрувати за часом від t1 до t2. На координатній площині (I2R, t) кількість виділеного тепла дорівнює площі криволінійної трапеції, яка зверху обмежена графіком залежності I2R = f(t). (див. рис. 44). Формула (4.13) – це закон Джоуля у звичайній формі. Вона
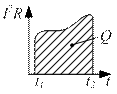
Рис. 44
визначає тепло, що виділилося у всьому провіднику. Можна перейти до диференційної форми закону Джоуля, яка характеризує виділення теплоти в різних місцях провідника:
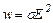, (4.14)
де 
– питома потужність струму, тобто кількість теплоти, що виділиться в одиниці об’єму в одиницю часу. З формули (4.14) випливає, що питома потужність пропорційна квадрату напруженості електричного поля Е. Знаючи питому потужність електричного струму, виділене у провіднику тепло визначається за формулою
,
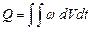де інтегрування ведеться по всьому об’єму провідника.
Правила Кірхгофа. Розгалуженні електричні кола легко розрахувати за допомогою двох правил Кірхгофа.
Перше правило. Алгебраїчна сума струмів, що збігаються у вузлі, дорівнює нулю
.
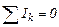Вузол – це точка розгалуженого електричного кола, де збігаються більше двох провідників. Струми, що входять у вузол, беруться з одним знаком, а що виходять – з протилежним.
Друге правило. При обході по замкненому контуру, що виділений у розгалуженому електричному колі, алгебраїчна сума добутків струмів на опір (тобто напруг на резисторах) дорівнює алгебраїчній сумі ЕРС у цьому контурі:
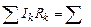Ek.
