Поскольку в системе чисел с плавающей точкой нарушаются основные законы арифметики, то при реализации алгоритмов на ЭВМ большую роль играет порядок организации вычислений, а именно: результат вычислений может сильно зависеть от порядка.
Алгоритм, в котором погрешность, допущенная в начальных данных или допускаемая при вычислениях, с каждым шагом не увеличивается или увеличивается незначительно, называется устойчивым. В противном случае, если погрешность существенно увеличивается от шага к шагу, алгоритм называется неустойчивым.
Чаще всего неустойчивость алгоритма связана с итерационными процессами, когда результат получается посредством последовательности итераций, причем на каждой итерации в качестве исходных данных используются значения, полученные на предыдущей итерации. Существуют неустойчивые алгоритмы, не связанные с итерационными процессами.
Пример. Известно, что ряд Тейлора для функции 
сходится для всех 
. Рассмотрим один из возможных алгоритмов суммирования этого ряда:
Шаг 1. Задать . 
; 
.
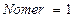Шаг 2. 
Шаг 3. Если 
= 
,
то вычисления закончены, результат -
иначе = , 
,
переход на шаг 2.
Проверка на шаге 3 учитывает то обстоятельство, что машинная арифметика является приближенной. Выражение будет иметь то же значение, что и , если число достаточно мало. Если провести вычисления по этому алгоритму для различных значений 
, получим числа, представленные в табл.1. Для 
эти числа соответствуют истинным значениям, но для 
картина неудовлетворительная: в некоторых случаях неверны даже знаки результатов. Это говорит о неустойчивости рассмотренного алгоритма.
Таблица1 –
|
|
|
|
| -1 -5 -10 -15 -20 | 2.718282 148.4132 22026.47 3269017. 4.8516531*108 0.3678794 6.7377836*10-3 -1.6408609*10-4 -2.2377001*10-2 1.202966 | 2.718282 148.4132 22026.46 3269017. 4.8516520*108 0.3678795 6.7379470*10-3 4.5399930*10-5 3.0590232*10-7 2.0611537*10-9 |
Пример. Необходимо вычислить 
При вычислении интеграла по частям получим:
,
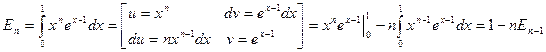т.е. 
. (10)
Предположим, что вычисления проводятся в системе чисел с плавающей точкой, для которой 
:
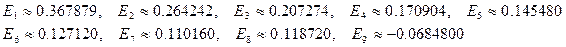
Поскольку для любого 
при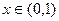 
: 
, то истинное значение 
. Что привело к ошибке? Единственная ошибка округления, сделанная в приведенных выше вычислениях, - это ошибка в 
, когда 
округляется до шести значащих цифр. Последующие значения 
получены округлением результатов, вычисленных точно по содержащему ошибку округления значению . Формула (10) точна для действительной арифметики, следовательно явная ошибка в 
всецело обязана ошибке округления в . Ошибка в - 
,
,
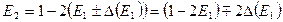т.е. ошибка в 
― 
. Аналогично, ошибка в 
― 
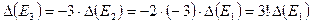и т.д. Ошибка в ― 
. Истинное значение 
. Таким образом, возникающая вследствие неустойчивости алгоритма ошибка – абсолютная погрешность – при вычислении значительно больше искомого значения , что не даст возможности получить ни одного верного знака в записи числа , что и наблюдается при вычислении по абсолютно точной с точки зрения обычной арифметики формуле (10).
Преобразуем формулу (10) эквивалентным образом:
. (20)
Теперь на каждом шаге вычислений ошибка в 
умножается на множитель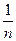 
. Таким образом, если начать вычисления с некоторого для 
и проводить вычисления в обратном порядке, то любая начальная ошибка или промежуточные ошибки округлений будут уменьшаться на каждом шаге, что говорит об устойчивости алгоритма, отвечающего (20).
Оценим значения в общем виде. Поскольку при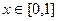 
: 
, то на сегменте 
: 
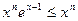, а значит:
, (25)
а это значит, что 
.
Таким образом, если в качестве стартового значения для вычислений в соответствии с формулой (20) взять, например, 
, значение которого положить равным нулю
, (30)
то начальная ошибка, допущенная при этом в (30), не превосходит в соответствии с (25)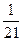 
. Эта ошибка умножится на 
при вычислении 
, так что ошибка в - 
.
Вычисления, проведенные по ормуле (20), приведут к следующему результату:
,
что говорит об устойчивости алгоритма (20).
Чувствительность задачи
Очевидно, что при решении произвольной реальной задачи в общем случае невозможно получить точное значение искомого численного результата. Существование неустранимой погрешности в математической модели объекта или процесса, фигурирующего в задаче, погрешности входных данных, многие из которых в реальных условиях получены экспериментально, погрешность метода, используемого для решения, и вычислительная, погрешности, возникающие при каких-либо дополнительных воздействиях на объект, которые часто трактуются как возмущения входных данных, приводят к необходимости их совокупного учета при оценке погрешности результата. Даже в случае, когда входные данные математической модели не имеют погрешностей, а метод, выбранный для решения полученной математической задачи является точным, избежать вычислительной погрешности при проведении вычислений в системе чисел с плавающей точкой, а значит и погрешности в полученном результате, невозможно. После построения математической модели реального процесса, которая необходимо удовлетворяет требованию адекватности (решение математической задачи, полученное с ее помощью, незначительно отличается от истинного решения реальной задачи), исходная задача и ее математическая формализация в процессе решения и анализа полученного результата, как правило, не разделяются. Однако, в силу особенностей машинной арифметики, невозможно в общем случае получить точное решение даже смоделированной математической задачи (пренебрегая неустранимой погрешностью и погрешностью метода).
Полученное приближенное (в силу перечисленных выше причин) решение некоторой вычислительной задачи 
может рассматриваться как точное решение, но другой, возмущенной задачи 
( отличается от возмущением входных данных). В этом случае для определения качества полученного приближения необходимо иметь возможность оценить степень зависимости решения от возмущений исходных данных.
Некоторые вычислительные задачи очень сильно «реагируют» на даже малые изменения данных, причем это не зависит от системы с плавающей точкой или выбранного алгоритма, а является свойством самой задачи.
Пример. Рассмотрим квадратное уравнение, корни которого являются «почти» кратными:
.
Корни уравнения: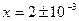 
. Изменение правой части уравнения лишь на 
вызовет изменение в корнях 
, т.е. на три порядка большее, чем начальное. Рассмотренная задача является чувствительной.
Назовем задачу чувствительной к погрешностям исходных данных, если даже малые погрешности исходных данных могут привести к значительной погрешности результата, и нечувствительной в противном случае.
Для чувствительных задач «правильные» ответы (ответы с очень малой погрешностью) принципиально нельзя получить никаким алгоритмом, поскольку даже малые ошибки, допущенные при представлении данных и при вычислениях (а эти ошибки сопровождают вычислительный процесс всегда) приведут к значительным погрешностям в результатах. В силу этого чрезвычайно важной и актуальной является численная оценка такой чувствительности, установления параметров, определяющих чувствительность, достаточных условий нечувствительности задачи.
Пусть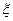 
― входные данные для некоторой задачи, результатом решения которой является 
; 
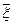― возмущенные входные данные, а решение задачи, полученное для этих входных данных, ― 
. Числом обусловленности задачи называется величина, определяемая соотношением:
. (2.1)
Очевидно, чем меньше число обусловленности, тем меньше возмущение результата зависит от возмущения входных данных, тем меньше чувствительность задачи, а при малом числе обусловленности задача окажется нечувствительной к погрешностям исходных данных. Таким образом, число обусловленности задачи является ее мерой чувствительности к возмущающим воздействиям.
Пример. Решить систему уравнений:
Предположим, что вычисления проводятся в системе с плавающей точкой, для которой 
. Решая систему методом Гаусса, получим:
.
При подстановке решения в исходную систему получим:
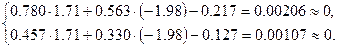
И хотя подстановка показала «хороший результат», точное решение системы, на самом деле, равно:
.
Вычисленное решение очень отличается от точного, хотя ведет себя примерно также, как точное. Рассмотренная задача является чувствительной (или плохо обусловленной, или некорректно поставленной).
