Методы решения задач линейного программирования.

Задачи линейного программирования

Программирование – процесс распределения ресурсов. Математическое программирование состоит в использовании математических методов и моделей для решения задач программирования.

Если цель исследования и ограничения на введенные переменные можно выразить линейными соотношениями, то соответствующая задача называется задачей линейного программирования (ЗЛП). Она относится к задачам оптимизации. Для решения таких задач вводится целевая функция, максимум или минимум которой нужно найти при ряде введенных ограничений – системы неравенств или равенств, определяющих область, в которой этот максимум или минимум ищется.

Постановка задачи линейного программирования.

1) ЗЛП в общем виде.

Необходимо исследовать на экстремум функцию

max (min) (1.1)

при условиях

(1.2)

Здесь и – заданные постоянные числа, .

Целевая функция (1.1) и ограничения в системе (1.2) являются линейными функциями от переменных , .

Целевая функция позволяет сравнивать различные варианты решений и выбрать тот вариант, при котором она достигает экстремального значения.

В матричной форме задачу (1.1) – (1.2) можно представить так:

max(min)

АХ b,

А – m n- матрица из коэффициентов при переменных в (1.2), b – m 1- матрица-столбец из свободных членов (1.2), Х – n 1- матрица-столбец из неизвестных.

ЗЛП в каноническом виде.

Оптимизировать функцию

max (1.3)

при условиях

АХ = b, (1.4)

(1.5)

где .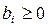

Для применения большинства методов решения задачу (1.1)-(1.2) необходимо привести к каноническому виду(1.3)-(1.5), используя следующие правила:

· Если необходимо минимизировать целевую функцию, т.е. решить задачу: , то для приведения к виду (1.3) необходимо изменить знак целевой функции: – .

· Условие , к виду (1.5) приводится заменой , где .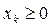

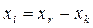· Условие любое число, к виду(1.5) приводится заменой , где .

· Ограничение, заданное неравенством вида АХ b, к виду (1.4) приводится введением дополнительной переменной : АХ + = b, где .

· Ограничение, заданное неравенством вида АХ b, к виду (1.4) приводится введением дополнительной переменной : АХ – = b, где .

Пример. Задача о диете.

Имеется два вида продуктов: x и y. Один килограмм продукта х стоит 25 рублей и содержит 10 единиц питательного вещества а и 12 единиц питательного вещества b. Один килограмм продукта у стоит 37 рублей и содержит 15 единиц питательного вещества а и 20 единиц питательного вещества b. Необходимый минимум в диете – 30 единиц а и 40 единиц b. Составить диету минимальной стоимости.

	х	у
а
b

Пусть Z – целевая функция. Тогда

Z = 25х + 37у min.

Введем ограничения на переменные:

Итак, если

- если система ограничений состоит из нестрогих неравенств стандартная

задача линейного программирования;

- если система ограничений состоит только из равенств каноническая задача;

- от стандартной задачи можно перейти к канонической добавлением новых вспомогательных переменных;

- при отыскании максимума или минимума нужно учитывать, что функция двух переменных достигает на выпуклом множестве максимум или минимум в точках пересечения границ, т.е. в вершинах многоугольника ограничений.

Методы решения задач линейного программирования.

Графический метод.

Постановка задачи:

Необходимо оптимизировать функцию

(2.1)

при условиях 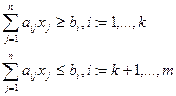(2.2)

(2.3)

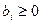где , и .

Если задача (2.1)-(2.3) содержит не более 3 переменных (n = 2), то ее решение можно легко найти графически по алгоритму, основанному на известных из курса математического анализа свойствах линейной функции двух переменных:

а) в выпуклой, замкнутой, ограниченной области линейная функция двух переменных достигает своего наибольшего и наименьшего значенийна границе этой области (в случае, когда область – выпуклый многоугольник – в одной из его вершин);

б) вектор grad f(x₁, х₂,…,х_n) = - вектор наискорейшего роста функции f(x₁, х₂,…,х_n) (при n=2: grad f(x,y) = )

вектор - grad f(x,y) - вектор наискорейшего убывания функции f(x,y);

в) вектор grad f(x,y) перпендикулярен линии уровня .

Алгоритм графического метода решения ЗЛП (вида (2.1)-(2.3)):

1. Построить множество допустимых решений, представленное системой ограничений (2.2). Это множество обычно является выпуклым и ограниченным.

2. Найти градиент grad f(x,y) целевой функции (2.1) в случае максимизации и (- grad f(x,y)) в случае минимизации.

3. Построить вектор градиента из начала координат.

4. Построить линию уровня целевой функции (2.1) – прямую , перпендикулярную вектору градиента, которая представляет график линейной функции (n = 2).

5. Перемещать линию уровня целевой функции параллельно себе вдоль вектора градиента до момента касания с границей множества допустимых решений в краевой точке. Точка касания является оптимальной.

6. Идентифицировать точку экстремума в зависимости от направления оптимизации функции.

Замечание.

· Если график линии уровня целевой функции имеет с границей множества допустимых решений одну общую точку, то задача имеет единственное решение.

· Если график линии уровня целевой функции имеет с границей множества допустимых решений две общих точки, то задача имеет бесконечное множество решений. При этом целевая функция будет достигать экстремума в любой точке множества, являющегося выпуклой комбинацией данных краевых точек.

· Если множество допустимых решений не ограниченно в направлении оптимизации целевой функции, то тогда задача не имеет решения.

Графически может быть решена ЗЛП с ограничениями в виде равенств. В этом случае, количество ограничений должно быть на два или три меньше количества переменных.

Постановка задачи:

Необходимо оптимизировать функцию

(2.4)

при условиях (2.5)

(2.6)

где 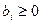. Необходимо выполнение условия: (или ).

Алгоритм графического метода решения ЗЛП (вида (2.4)-(2.6)):

1. Привести систему ограничений (2.5) к виду

(2.7)

Переменные называются базисными (или базисом), при этом каждая переменная присутствует только в одном уравнении с коэффициентом +1 и отсутствует в остальных уравнениях. Переменные называются небазисными.

2. Выразить базисные переменные через небазисные:

, . (2.8)

3. Заменить базисные переменные в целевой функции на их выражение через небазисные (2.8). Получим новую целевую функцию:

(2.9)

4. Используя неравенство (2.6), получим , , тем самым перейдем к системе ограничений (2.10):

(2.10)

(2.11)

5. Выполнить шаги 1-6 алгоритма графического метода решения ЗЛП (вида (2.1)-(2.3)) для задачи (2.9)-(2.11).

6. Найти значения базисных переменных по формуле (2.8). Вектор является решением исходной задачи (2.4)-(2.6).

Пример 1. Шоколадная фабрика (целью которой является максимизация прибыли) производит два вида продукции: шоколад и конфеты (рыночная цена которых 4 и 5 тыс. у.е. за тонну), из двух видов сырья: какао-бобов и орехов. За один период фирма может закупить не более 12 тонн какао-бобов и 8 тонн орехов. При этом для производства 1 тонны шоколада необходимо 5 т. какао-бобов и 2 т. орехов, а для производства 1 т. конфет 2 т. какао-бобов и 4 т. орехов. Сколько тонн шоколада и конфет нужно произвести, чтобы прибыль фабрики была наибольшей?

Решение. Составим модель производства продукции. Обозначим производимые продукты за x (шоколад) и y (конфеты). Т.к. целью фирмы является максимизация прибыли, целевой функцией следует выбрать функцию прибыли данного предприятия.

Соответственно, на производство шоколада потребуется 5 x т. какао-бобов, а на производство конфет 2 y т. При этом может быть затрачено не более 12 т. данного сырья.

Аналогично и для второго ингредиента – орехов: ;

Т.о. решаемая задача принимает вид

Система описывает множество пар объемов продукции, которые может производить фирма при ограниченных ресурсах.

Решим данную задачу графически.

Рис.1.

Ответ: Шоколадная фабрика должна произвести 2 тонны шоколада и 1 тонну конфет, чтобы прибыль была наибольшей.

Применим графический метод для решения задачи.

Пример 2. С целью обеспечения высокого объема перевозок железная дорога имеет возможность рекламировать свою деятельность, используя местные радио и телевизионные сети. Затраты на рекламу ограничены величиной 3000 условных денежных единиц. Каждая минута радиорекламы обходится в 20 условных денежных единиц, а минута телерекламы – в 60 единиц. Исходя из своих конъюнктурных соображений, железная дорога хотела бы использовать радиосеть по крайней мере в 2 раза чаще, чем телесеть. Радиокомпания согласна предоставить рекламное время в объеме не более 100 минут. Одна минута телерекламы обеспечивает объем перевозок в 6 раз превышающий объем перевозок, обеспечиваемый радиорекламой. Найти оптимальное распределение финансовых средств между телевизионной и радиорекламой.

Обозначим за х ₁ и х ₂ количество времени, затрачиваемого на радио и телерекламу, соответственно. Если W – объем перевозок, обеспечиваемый 1 мин. радиорекламы, а z – общий объем перевозок, то целевая функция может быть записана в виде

.

Так как величина W считается постоянной, вместо функции можно рассматривать функцию

,

максимум, которой в некоторой области достигается в тех же точках, что и функцией .

Из условия задачи можно записать ограничения в виде неравенств, связанные с ограниченностью средств на рекламу

,

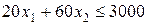а так же с конъюнктурными интересами железной дороги

.

Кроме того, имеются ограничения, связанные с объемом времени на рекламу

; ; .

Таким образом, рассматриваемая задача записывается в виде

(2.4)

(2.5)

Каждое из неравенств описывает полуплоскость, и областью решений системы будет многоугольник, являющийся пересечением всех пяти полуплоскостей. Границы полуплоскостей описываются равенствами.

20 х ₁+60 х ₂=3000

х ₁-2 х ₂=0

х ₁=100 (2.6)

х ₁=0

х ₂=0

y=60

x₁

Рис. 2.

Решение системы неравенств (2.5) образует на плоскости четырехугольник OPRS, а целевая функция при различных значениях у образует на плоскости параллельные прямые (рис. 2.2). При этом значение у возрастет в направлении вектора

Отыскав направление возрастания функции у, будем перемещать вдоль этого вектора прямую, соответствующую целевой функции у, до тех пор, пока она не выйдет за пределы области OPRS. Это происходит в точке P, в которой и достигается максимальное значение функции у (а вместе с ней и z) в области OPRS.

Уточним координаты точки Р. Для этого учтем, что она является точкой пересечения прямых, описываемых уравнениями

Решив систему, найдем координаты точки Р (60;30). Это означает, что для получения наибольшего объема перевозок необходимо выделить средства на 60 мин. радиорекламы в размере 1200 условных единиц и на 30 мин. телерекламы в размере 1800 условных единиц.

Замечание. Иногда задача имеет не одно оптимальное решение. Это возможно, когда прямая, изображающая целевую функцию, параллельна одной из границ области допустимых значений.

Симплекс – метод.

Рассмотрим на примере.

F = х₁+х₂_→ max

х₁-х₂ ≤ -2 х₁-х₂+х₃ = -2

х₁-2х₂ ≥ -13 х₁-2х₂- х₄ = -13

3х₁-х₂≤ 6 3х₁-х₂+х₅ = 6

х₁ ≥ 0, х₂ ≥ 0 х₁≥ 0, х₂ ≥ 0

а) приведем задачу к каноническому виду;

б) учтем, что х₁и х₂ – основные переменные (они входят в целевую функцию), х₃, х₄ и х₅ – неосновные переменные.

Выразим неосновные переменные через основные:

-х₁+х₂-2 = х₃

х₁-2х₂+13 = х₄

-3х₁+х₂+6 = х₅

х₁ ≥ 0, х₂ ≥ 0 F = х₁+х₂

в) составим симплекс – таблицу:

-х₁ -х₂ b

х₃ -1 -2

х₄ -1

х₅ -1

F -1 -1

Переменные x_1,x₂включаются в таблицу с коэффициентом + для задачи минимизации и с коэффициентом - для задачи максимизации. Если последний столбец и последняя строка не содержат отрицательных чисел, то получен ответ. В противном случае проводится МЖИ (метод модифицированных жордановых исключений) – процедура, с помощью которой избавляются от отрицательных чисел сначала в последнем столбце, затем в последней строке. В последнем столбце выбираем любой отрицательный элемент (например: -2) и движемся по строке, в которой он расположен. Берем любой отрицательный элемент в этой строке (например: -1), который расположен во втором столбце (разрешающий столбец). Далее поэлементно делим последний столбец на разрешающий столбец. Из положительных полученных отношений берем наименьшее (min = 2). Строка, в которой достигается минимум, называется разрешающей. Элемент, расположенный на пересечении разрешающей строки и разрешающего столбца, называется разрешающим (-1);

г) преобразуем таблицу. Для этого

а) в разрешающей строке и разрешающем столбце переменные меняем местами (т.е. х₂ и х₃);

-х₁ -х₃ b

х₂ -1 -1

х₄

х₅ -1

F -2 -1

б) на месте разрешающего элемента (-1) пишем 1/ разрешающий элемент (1:(-1) = -1);

в) в разрешающей строке каждое число (кроме (-1)) делим на разрешающий элемент;

г) в разрешающем столбце каждое число (кроме (-1)) делим на разрешающий элемент и результат берем со знаком минус;

д) остальные элементы считаем по правилу прямоугольников:

старый элемент разрешающий элемент -

новый элемент = ----------------------------------------------------------------,

разрешающий элемент

старый элемент

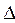
разрешающий элемент

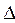- элемент разрешающей строки (в одном столбце со старым),

- элемент разрешающего столбца (в одной строке со старым).

е) последний столбец не содержит отрицательных чисел, но в последней строке отрицательное число есть. Выбираем большее по абсолютной величине, т.е. -2. Тогда первый столбец разрешающий. Делим последний столбец на разрешающий и из положительных полученных отношений выбираем min разрешающая строка – третья, а 2 - разрешающий элемент;

ж) в разрешающей строке и разрешающем столбце переменные меняем местами (т.е. х₁ и х₅); повторяем расчеты;

-х₅ -х₃ b

х₂ 0,5 -1,5

х₄ -0,5 2,5

х₁ 0,5 -0,5

F -2

з) снова повторяем расчеты:

-х₅ -х₄ b

х₂ 0,6

х₃ -0,2 0,4

х₁ 0,2

F 0,6 0,8

Последний столбец и последняя строка не содержат отрицательных чисел задача решена:

х₁= 5, х₂ = 9, х₃= 2 F = 14 – 0,6 *х₅– 0,8*х_4,

F_max=14, Х=(х₁, х₂, х₃, х₄, х₅) = (5,9,2,0,0).

Ответ: F_max=14, х₁= 5, х₂ = 9.

Критерии оптимальности решения при отыскании максимума целевой функции: если в выражении линейной функции через неосновные элементы отсутствуют положительные коэффициенты при этих элементах, то решение оптимальное. В данном случае получено оптимальное решение.