Ции).
Сложные и очень сложные производственные, экономические, биологические и другие системы должны строиться и рассматриваться как системы, реализующие принцип самоорганизации. Такие системы представляют собой прочно связанное информационными и энергетическими связями единое целое. Отличительной особенностью любой такой системы является рассмотрение ее только как единого организма, что позволяет реализовать единый подход к системам не только различного назначения, но и различной физической природы, в том числе к неодушевленным и одушевленным системам. Такая возможность базируется на общности типа связей между элементами даже чрезвычайно разнородных систем. Это информационные и энергетические связи, так что с позиции преобразования информации и энергии, необходимой для этого, сложные, искусственно создаваемые, и естественные, природно существующие, системы однородны.
Принцип самоорганизации реализуется в любых системах за счет наличия в них обратной связи.
Термин «обратная связь» достаточно полно определяет вложенный в него смысл. Однако истинное значение механизма обратной связи для систем осознается явно недостаточно даже специалистами, что находит отражение в низкой эффективности ряда искусственно созданных систем. Отсюда следует вывод, что в идее обратной связи скрыта определенная сложность, которая является препятствием для ее понимания и ограничивает ее применение в промышленных, экономических и социальных системах.
Рассмотрим идею обратной связи на простейшем примере. В качестве примера используем обратную связь в простой детерминированной системе –
регуляторе Уатта. В течение более двухсот лет этот механизм служит наглядным подтверждением простоты и изящества обратной связи и демонстрирует ее эффективность в регуляторе. В то же время можно утверждать, что истинное значение этого изобретения еще не полностью осознано.
Маховик парового двигателя вращается с возрастающей скоростью, вместе с ним также с возрастающей скоростью вращаются рычаги с грузами. Эти рычаги управляют клапаном, через который производится впуск пара в цилиндр двигателя таким образом, что степень открытия клапана пропорциональна уровню подъема рычагов или, что то же самое, скорости. Следовательно, имеет место гомеостат, так как чем больше двигатель стремится превысить требуемую скорость, тем меньше энергии поступает в него. В то же время при отклонении от заданной скорости в другую сторону приток энергии увеличивается, пока заданная скорость ни будет достигнута. Таким образом, заданное значение скорости достигается путем саморегулирования: вход двигателя подстраивается его выходом и оба этих сигнала приобретают установившиеся значения.
Что же недооценено в действии этого простого механизма?
Прежде всего следует обратить внимание на то, что регулятор с обратной связью ведет себя почти как одушевленный организм: он всегда и точно выполняет возложенные на него функции. При использовании его невозможно представить, чтобы переменные выходили за заданные пределы. Это объясняется тем, что само движение за пределы ограничений вызывает появление управляющего воздействия. Следовательно, регулятор с обратной связью не может не справиться с возложенной на него задачей.
Но еще более важным является вытекающее отсюда следствие, заключающееся в том, что регулятор с обратной связью гарантирует компенсацию возмущений не только определенного вида, но и любых возмущений вообще. Регулятор с обратной связью реагирует не большое число источников возможных возмущений. Он компенсирует влияние на систему возмущений, причина возникновения которых совершенно неизвестна. В этом как раз и заключается важность принципа обратной связи, поскольку приходится иметь дело с очень сложными системами не поддающимися детальному описанию. Чтобы получить возможность управлять такими системами необходимо предусмотреть механизм, способный выполнять функции, которые не ясны исследователю.. Но именно эти функции и может выполнять регулятор с обратной связью. Отсюда вытекает его важнейшая роль и то значение, которое он сыграл в названии науки об управлении, т.е. кибернетики. (Регулятор по латыни следует от латинского слова «управляющий», которое в свою очередь образовано от греческого слова «кибернесий», что означает кормчий).
Приведенный пример обратной связи в регуляторе Уатта иллюстрирует «отрицательную» обратную связь. Термин «отрицательная» объясняется тем, что если рассогласование между действительным и заданным значениями гомеостатического параметра машины (в данном случае скорости вала двигателя) определяется как положительная величина, то действие обратной связи имеет противоположный знак.
Из приведенного следует, что системы любой физической природы могут
рассматриваться с единых позиций, а именно как самоорганизующиеся, для
которых характерна:
- сложность;
- открытость (функционирование во взаимодействии с окружающей сре-
дой);
- существенная нелинейность (за счет которой реализуется обратная
связь).
Таким образом, возникла новая парадигма, новая система взглядов на окружающий мир- синергетика.
Синергетика – не отдельная наука. Она родилась не на пустом месте.
Большинство известных результатов и используемых методов анализа полу-
чено в теории колебаний, в гидродинамике, в термодинамике учеными, ре-
шившими конкретные задачи и не причислявшими себя к новому направле-
нию. Именно это обстоятельство служит поводом для неприятия некоторыми
синергетики как нового направления. Но теория колебаний и гидродинамика
являются отдельными направлениями физики, а не самостоятельными наука-
ми. Синергетика – это следствие озарения гения давно известными, накопив-
шимися в разных науках результатами, который обратил внимание именно на общность некоторых систем в процессе их самоорганизации.
Итак, синергетика – это новая система взглядов на явления жизни, рас-сматривающая живое и неживое как единое целое на основе идеи самоор-
Ганизации.
Проиллюстрируем некоторые возможности синергетического подхода к
решению творческой задачи на простом примере. Рассмотрим функциони-
рование биологической системы, представляющей собой популяцию живот-ных с позиции динамики ее численности.
Первоначально построим и исследуем наиболее простую математическую модель этой системы. Она может быть представлена в виде линейного одно-
родного дифференциального уравнения.
=kN(t) (1.1)
где:
N(t) – текущая численность популяции;
k = const – коэффициент пропорциональности, отражающий влияние рождае-
мости и смертности на численность популяции.
Уравнение (1.1) имеет решение (1.2).
N(t) = N(0) 
(1.2),
График, соответствующий решению (1.2) представлен на рис.1.2.
Рис. 1.2.
При построении модели система рассматривалась как простая, закрытая и
линейная. Здесь не использовалась ни одна из синергетических посылок и полученный результат не имеет ничего общего с реальной ситуацией.
Введем теперь в модель нелинейность, которая сыграет роль обратной связи и позволит в определенной мере отразить самоорганизацию, прису-щую реальной системе.
В этом случае математическая модель системы запишется в виде нелиней-
ного дифференциального уравнения (1.3).
= k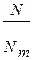 
(Nm– N) (1.3)
где Nm характеризует «емкость» среды, т.е. это – численность популяции,
которую окружающая среда может прокормить.
Полученное уравнение сводится к табличному интегралу вида
= - 
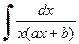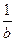ln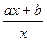 
и легко интегрируется. В результате имеем:
N(t)=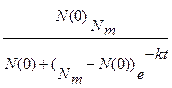 
(1.4)
Пусть N(0)= 
, тогда из (1.4) следует N(t)=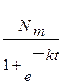 
.
График, соответствующий (1.4), представлен на рис.1.3.
Рис.1.3.
Полученный результат достаточно близок к реальной ситуации.
Теперь воспользуемся еще одной синергетической посылкой, а именно: будем рассматривать систему как открытую и применим широко используемый в теории колебаний качественный анализ дифференциальных уравнений. С целью большей простоты и наглядности используем нелинейную модель иного вида:
=k(t)N(t) (1.5)
где:
k(t) – коэффициент, учитывающий изменяющиеся условия взаимодействия
системы с окружающей средой.
k(t)= a – bN(t). Тогда:
=aN(t) – bN2 (t)
Здесь aN(t) отражает темп прироста популяции, а bN2 (t) – темп вымирания.
Пусть a=1 и b=1, тогда
=N(t) – N2 (t) (1.5а).
Из анализа (1.5а) следует, что в данной системе возможны два установив-
шихсяравновесных состояния, определяемые условием:
=N(t) – N2 (t) = 0.
Данное равенство дает координаты этих состояний: N01 =0; N02 =1. Это же
равенство определяет, что >0, а следовательно N(t) возрастает при
0<N(t)<1; что <0, а следовательно N(t) убывает при N(t)>1.
Такой качественный анализ дает возможность построить следующую картину возможных событий в системе.
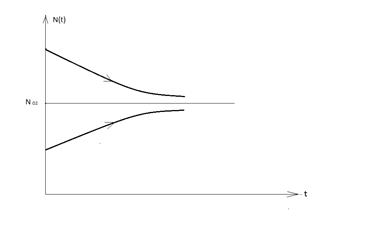
Рис.1.4.
Из приведенного следует, что в системе существуют два равновесных сос-
тояния, одно из которых (N02 =1)является абсолютно устойчивым с областью
притяжения от нуля до бесконечности, а второе (N01 =0) – неустойчивым.
Уточним модель, и введем в нее показатель, отражающий уменьшение популяции за счет неучитываемых ранее факторов взаимодействия с окружающей средой(например – охота). В этом случае модель системы примет вид
=N(t) – N2 (t) –C (1.6)
где C – квота на отстрел (отлов).
Установившиеся равновесные состояния определяет решение уравнения
N – N2 – C = 0, т.е. N(1,2) =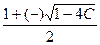 
(1.6а)
Из (1.6а) следует, что значение С качественно изменяет характер поведе-
ния системы, а именно:
а). При С<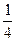 
уравнение (1.6а) имеет два действительных корня, причем оба
они положительны. Картина поведения системы полностью аналогична рас-
смотренному ранее и представлена на рис.1.5.
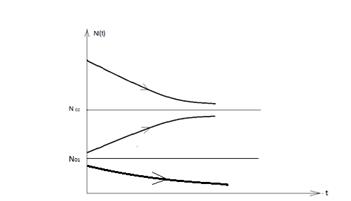
Рис.1.5
б). При С> 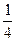уравнение (1.6а) имеет пару комплексно-сопряженных корней.
Такие условия невозможно организовать на практике.
в). При С= 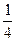уравнение (1.6а) имеет действительный кратный корень
N1(2) = 
. Картина поведения системы представлена на рис.1.6.
Рис.1.6.
Выполним последнее уточнение модели, введя в отстрел (отлов) элемент саморегулирования, а именно будем считать С пропорциональным числу особей в популяции, т.е. С=mN.
В этом случае имеем
=N(t) – N2 (t) –mN(t) (1.7)
Координаты установившихся равновесных режимов определим, задаваясь
значением m= . Будем иметь N1(2) = . При этом, для всех N(0)>
<0, а для всех N(0)< >0. Картина поведения системы представлена на рис.1.7. Она свидетельствует о том, что найденное решение
является рациональным и позволяет обеспечить выживание популяции при
любых начальных условиях.
Рис.1.7.
