Идея этого метода криптографии заключается в том, что запись открытого текста и последующее считывание шифровки производится по разным путям некоторой геометрической фигуры (например, квадрата).
Для пояснения идеи возьмем квадратную таблицу (матрицу) 8 ´ 8, будем записывать текст последовательно по строкам сверху вниз, а считывать по столбцам последовательно слева направо.
Предположим, что требуется зашифровать сообщение:
НА ПЕРВОМ КУРСЕ ТЯЖЕЛО УЧИТЬСЯ ТОЛЬКО ПЕРВЫЕ ЧЕТЫРЕ ГОДА ДЕКАНАТ.
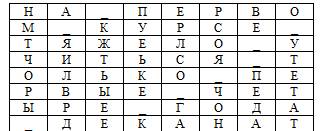
В таблице символом «_» обозначен пробел.
В результате преобразований получится шифровка
НМТЧРЫ_А_ЯИЛВРД_КЖТЬЫЕЕПУЕЬКЕ_КЕРЛСО_ГАРСОЯ_ЧОНВЕ__ПЕДАО_УТЕТАТ.
Как видно из примера, шифровка и открытый текст содержат одинаковые символы, но они располагаются на разных местах.
Ключом в данном случае является размер матрицы, порядок записи открытого текста и считывания шифрограммы. Естественно, что ключ может быть другим. Например, запись открытого текста по строкам может производиться в таком порядке: 48127653, а считывание криптограммы может происходить по столбцам в следующем порядке: 81357642.
Будем называть порядок записи в строки матрицы ключом записи, а порядок считывания шифрограммы по столбцам – ключом считывания.
Тогда правило дешифрирования криптограммы, полученной методом перестановок, можно записать так.
Чтобы дешифровать криптограмму, полученную с помощью матрицы n x n, нужно криптограмму разбить на группы символов по n символов в каждой группе. Крайнюю левую группу записать сверху - вниз в столбец, номер которого совпадает с первой цифрой ключа считывания. Вторую группу символов записать в столбец, номер которого совпадает со второй цифрой ключа считывания и т.д. Открытый текст считывать из матрицы по строкам в соответствии с цифрами ключа записи.
Рассмотрим пример дешифрации криптограммы, полученной методом перестановок. Известно, что при шифровании использованы матрица 6х6, ключ записи 352146 и ключ считывания 425316. Текст шифрограммы таков:
ДКАГЧЬОВА_РУААКОЕБЗЕРЕ_ДСОХТЕСЕ_Т_ЛУ
Разобьем шифрограмму на группы по 6 символов:
ДКАГЧЬ ОВА_РУ ААКОЕБ ЗЕРЕ_Д СОХТЕС Е_Т_ЛУ
Затем первую группу символов запишем в столбец 4 матрицы 6x6, так как первая цифра ключа считывания – 4 (см. рисунок а). Вторую группу из 6 символов запишем в столбец 2 (см. рисунок б), третью группу символов – в столбец 5 (см. рисунок в), пропустив две фазы заполнения матрицы, изобразим полностью заполненную матрицу (см. рисунок г).
Считывание открытого текста в соответствии с ключом записи начинаем со строки 3, затем используем строку 5 и т.д. В результате дешифрования получаем открытый текст:
ХАРАКТЕР ЧЕЛОВЕКА СОЗДАЕТ ЕГО СУДЬБУ
Естественно, что описанная процедура дешифрования криптограммы производится компьютером автоматически с помощью заранее разработанных программ.

Для повышения криптостойкости методы замены и перестановки нередко используют в сочетании с аддитивным методом.
При шифровании аддитивным методом вначале открытый текст шифруют методом замены, преобразуя каждую букву в число. Затем к каждому числу добавляют секретную гамму (псевдослучайную числовую последовательность). Технически добавление гаммы в криптографических системах осуществляется поразрядно (поточный шифр): на каждый бит открытого текста поочередно накладывается бит секретной гаммы.
Генератор потока ключей – гаммы выдает поток битов:g1, g2, g3,…, gi. Этот поток битов и поток битов открытого текста p1, p2, p3,…, pi подвергаются поразрядно логической операции Исключающее ИЛИ. В результате получается поток битов шифротекста:
ci = pi Å gi.
При дешифровании операция Исключающее ИЛИ выполняется над битами шифротекста и тем же самым потоком гаммы:
pi = ci Å gi.
В ЭВМ преобразование открытого текста в числа происходит естественным путем, так как каждый символ кодируется двоичным числом. Вид этого преобразования зависит от используемой операционной системы. Для определенности будем считать, что сообщение в ЭВМ кодируется с помощью кодовой таблицы CP-1251. Итак, будем считать, что секретная гамма добавляется к открытому тексту по правилу сложения по модулю два без переносов в старшие разряды (логическая операция Исключающее ИЛИ). Результаты всех преобразований поместим в таблицу.

Для наглядности результат шифрования (шифрограмма) переведен с помощью таблицы CP-1251 в буквы. Из таблицы видно, что открытый текст был записан прописными буквами, а криптограмма содержит как прописные, так и строчные буквы. Естественно, что при реальном (а не учебном) шифровании набор символов в шифрограмме будет еще богаче. Кроме русских букв будут присутствовать латинские буквы, знаки препинания, управляющие символы.






