Распространение ур-я Бернули для струйки на поток жидкости.
Z1+P1/ρg+U1^2/2g= Z2+P2/ρg+U2^2/2g+hтр можно исп-ть лишь на потоке, наз-ом параллельно струйными или плавноизменяющие. Плавноизменяющиемся движ-е хар-ся:
1.расхождением соседних струек 2.кривизна линии стока настолько мала, а R загружения велико, что центробежными силами можно пренебречь. 3.кривизна сечения потока из-за неравномерности распределения скоростей можно рассм-ть как плоские.
Получить з. распр-я гидродинамического давления можно используя диф-е ур-я движ-я жид-ти:

 X-
X-  -
-  =0 Uy=0 u Uz=0 =>
=0 Uy=0 u Uz=0 =>
y- 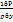 -
-  =0 y-
=0 y- 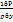 -
-  =0
=0
z- 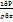 -
-  =0 z-
=0 z- 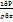 -
-  =0 (1)
=0 (1)
(1)Подчиняется гидростат-му з. Z+P/ρg =const; P=Po+ρgh Корректив кинетич-ой энергии: α=Ек(u)/Ек(υ); α=  Полный напор в сечении потока: H̕ ̶>H – полный напор Z+P/ρg+U^2/2g=H́ - надо осреднить по всему сечению потока ω. Для этого: 1.умн-ем H́ на все жид-ти протекающие за время dt. 2.интегрируем это выр-е по всей пл-ти живого сеч-я ω для получения полной энергии V. 3.делим получ-ю энергию на все жид-ти для потока и получ-ем удельную энергию,относит-о которой 1-ца жид-ти проходит через сечение потока ω за время dt и наз полным потоком.
Полный напор в сечении потока: H̕ ̶>H – полный напор Z+P/ρg+U^2/2g=H́ - надо осреднить по всему сечению потока ω. Для этого: 1.умн-ем H́ на все жид-ти протекающие за время dt. 2.интегрируем это выр-е по всей пл-ти живого сеч-я ω для получения полной энергии V. 3.делим получ-ю энергию на все жид-ти для потока и получ-ем удельную энергию,относит-о которой 1-ца жид-ти проходит через сечение потока ω за время dt и наз полным потоком.

 15. геометрическая и энергетическая интерпритация ур-я Бер-и для потока реальной жид-ти. P P
15. геометрическая и энергетическая интерпритация ур-я Бер-и для потока реальной жид-ти. P P


 P1/pg P2/pg
P1/pg P2/pg



 1 2
1 2
Z1 Z2
0 0
Z+P/ρg->H̕; Hp̕-изометрический напор Р-Р – пьезометрическая линия
 z - геометрическая высота или геометрический напор, м; P/g — пьезометрический напор или пьезометрическая высота, м; u2/(2g)=hu —скоростной напор м; Н —полный напор,м
z - геометрическая высота или геометрический напор, м; P/g — пьезометрический напор или пьезометрическая высота, м; u2/(2g)=hu —скоростной напор м; Н —полный напор,м

 в
в


 а U^2/2g
а U^2/2g











dl

 Zа+Pа/ρg+Uа^2/2g=Zб+Pб/ρg+Uб^2/2g
Zа+Pа/ρg+Uа^2/2g=Zб+Pб/ρg+Uб^2/2g
 Е1 Е2 Uб=0; Pб/ρg-Pа/ρg= Uа^2/2g hu
Е1 Е2 Uб=0; Pб/ρg-Pа/ρg= Uа^2/2g hu
Uа^2/2g-удельная кинет.энергия Энергетический смысл ур-я Бернулли: для элем-ой струйки идеальной жид-ти полная удельная энергия, равная сумме удельной потен-ой энергии давления, удельной потенц-ой энергии положения и кинетической удельной потенциальной энергии положения и кинетической удельной энергии, есть вел-а постоянная во всех сеч-х по отношению к выбранной пл-ти отсчета. Для реальной жид-ти напор всегда будет > напора в последующих сечениях, т.к. часть энергии затрачивается на преодал-е сил сопр-я.
общие сведенья о потере напора.режимы движ-я жид-ти.Осн-е ур-я равномерного движ-я жид-т.
Гидравлические потери — безвозвратные потери удельной энергии(переход её в теплоту) на участках гидравлических систем, обусловленные наличием вязкого трения Сущ-ет 2 вида движ-я: ламинарное(движ-е струйное или по слоям) и турбулентное(частицы жид-ти перемешиваются). Поскольку при турбулентном режиме течения происходит расход энергии потока на преодоление вязкости при турбулентных колебаниях, гидравлические потери при ламинарном режиме течения жидкости значительно меньше, чем при турбулентном. благодаря числу рейнольдса можно установить режим течения. Re=Vl/ν ν -коэф-т вязкости. Для некруглых сечений и для труб, работающих неполным сечением: Rer= VR/ν; R-гидравлический радиус = отношению площади живого сечения к смоченному периметру. R=w/χ для потока каналов некруглого сечения смена режима течения происходит при числе рейнольдса Reкр, вел-а к-го с учетом гидравлического радиуса R=d/4 равна Reкр=2320/4=580 При Re>Reкр –турбулентное, Re<Reкр –ламинарное.







 τ0
τ0
τ-сила тр-я на единицу площади смачиваемой пов-ти русла.
τ0=pgIR- осн-е уравнение
I-гидравлический уклон. I=h/l R-гидравлический радиус R= w/χ
17.распред-е скоростей в сечении потока,потери напора по длине при ламинарном движ-и,потеря давления. При ламинарном режиме движ-я жид-и в круглой трубе, скорости в попер-ом сечении распределены по параболе, скорости у стенок трубы равны 0 и, плавно увеличиваясь, достигают максимума на оси потока.Частицы жид-ти соприкасаются с тв-ой пов-ью трубопровода явл-я прилипшими к нему и скорость U=0.воспользовшись осн-ым ур-ем равномерного движ-я: τ=+-µ*dU/dr; τ=pgIR; R=r*1/2;приравняв эти выражения получим pgIRr/2=- µ*dU/dr dU= pgIR*r/2*1/µ dr; U=1/2*pg/µ*I*1/2*r^2+C C=1/4* pg/µ*I*r0^2; U=1/4* pg/µ*I(r0^2-r^2) r=r0 U=0; r=0 U=max Umax=1/4* pg/µ*I*r0^2=1/16* pg/µ*I*d^2-максимальная скорость. Опр-им элем-ый расход жид-ти. dQ=Udω=1/4* pg/µ*I(r0^2-r^2)*2πr*dr Q=∫1/4* pg/µ*I(r0^2-r^2)*2πr*dr=1/8*pg/µ*I* πr0^4 V=Q/ω; V=1/128*pg/µ*I* πd^4; V=1/32* pg/µ*h/l*d^2 h=Vµl32/ρgd^2 Потеря напора по длине пропорциональна ср-ей скорости(1-ой степени)
h=Vµl32/ρgd^2 *(Vr*V/2V)=64/Re*(C*V^2/2g) 64/Re=λ- коэф-т гидравлического трения h=λ*l/d*V^2/2d/g
18.Общие сведенья о турбулентном потоке. В турбулентном потоке скорость в любой т-е постоянно изменяется около ср-го знач-я по вел-е и напр-ю это явл-е наз-я пульсацией скорости. В связи с этим тур-е движ-е явл-я не установившимся его кинетические и динамические хар-ки рассм-я как случайные фун-ции.
При тур-ом движ-и скорость осредняется дважды: начало осредняется в точке(чтобы получить осредненную составляющую предельнуб), а затем осредняют полученные осредненные скорости.
При тур-ом движ-и возможны шероховатости ламинарным подслоем толщиной δ и зависит от степени движ-я потока, хар-ся числом Re. При большом Re δ→0-разрушается.
Если δ>=Δ-гидравлически гладкая, δ<=Δ- гидравлически шероховатая.
Δ- шероховатость.
19.Зоны сопротивления движ-ю жид-ти. 1.зона вязкого сопр-я. ламинарный режим движ-я. Предел по числу рейнольдса Re<2320. Коэф-т λ зависит только от Re λ =Re/64. Потери напора равны: hдл=64ν/Vd*l/d*V^2/2g=kV: k-кожэф-т пропорциональности. Под эквива-лентной шероховатостью Ази» понимают такую высоту выступов шероховатости, сложенной из песчинок одинакового размера, которая при экспериментах дает одинаковую с естественной абсолютной шероховатостью вел-у коэф-а гидравлического тре-ния. В области гидравлически гладких труб при 2320 < Re < 20d/Аэкв 2-я зона - гладкостенного сопр-я. В этой зоне пристенный слой, толщина которого 5 больше шероховатости Δ, имеет структуру ламинарного течения. Коэф-т сопр-я λ зависит только от числа Re, т. е. λ, = f(Re). В этой зоне hдл=kV^1/75. Численное знач-е коэф-а λ можно опр-ть по ф-е Блазиуса: λ=0.3164 /Re^0.25 3-я зона - переходная от гладкостенного сопр-я к квадратичному, в которой на коэф-т λ оказывают влияние 2 фактора: число Re и относительная шероховатость.hдл=kV^1.75-2.0 20 d/ Δ экв<Re<500 d/ Δ экв Для опр-я λ, в этой зоне может быть рекомендована ф-ла А.Д. Альтшуля: λ=0.11(68/Re+d/ Δ)^0.25 4-я зона - квадратичного сопр-я при которой влиянием вязкости жид-ти на вел-у сопр-я можно пренебречь, а это значит, что коэф-т λ будет зависеть только от относительной шероховатости. hдл=kV^2.0; Re >500 d/ Δ экв Коэф-т λ в этой зоне можно опр-ть по ф-ле Б.Л. Шифринсона: λ= 0,11 (d/ Δ)^0.25
20.коэф-т гидравлического трения.ф-лы для его опр-я. Для опр-я коэф-а λ предложен ряд ф-л, учитывающих его зависимость от числа Рейнольдса, шероховатости,размеров поперечного сечения труб. Экспериментальными работами И. Никурадзе и А.П. Зегжда, посвященными изучению гидравлических сопр-ий в трубах с искусственной шереховатостью, было установлено существование четырех основных зон сопр-ий*, каждая из которых характе-ризуется своими зависимостями λ=f(Re,). В общем случае λ зависит от Re и шероховатости стенок трубы. 1 зона вязкого сопр-я. λ =Re/64 2-я зона - гладкостенного сопр-я λ=0.3164 /Re^0.25 3-я зона - переходная от гладкостенного сопр-я к квадратичному λ=0.11(68/Re+d/ Δ)^0.25 4-я зона квадратичного сопр-я λ= 0,11 (d/ Δ)^0.25
21.Потеря напоро по длине при тур-ом движ-и. ф-ла шези,ее практическое использование.потеря давления по длине. Потери напора зависит конкретно от зон сопротивления. Для квадратичной зоны, когда знач-е λ не зависит от Re получена ф-ла шези для опр-я потерь h=λ*l/d*V^2/2g; d=4R; V= 
h/l=I=i→  =c- коэф-т Шези.
=c- коэф-т Шези.
V=c*  - в-ла Шези. С зависит только от шероховатости как и коэф-т трения λ. С=1/nэк*R^1/6 nэк-знач-е справочное n=0.021..0.025 h=il→i=V^2/c^2R; c^2R=W h= V^2/c^2R*l Q=wc
- в-ла Шези. С зависит только от шероховатости как и коэф-т трения λ. С=1/nэк*R^1/6 nэк-знач-е справочное n=0.021..0.025 h=il→i=V^2/c^2R; c^2R=W h= V^2/c^2R*l Q=wc  ;i=(Q^2/R^2)*l
;i=(Q^2/R^2)*l
Отсюда, h =(Q^2/R^2)*l –ф-ла Шези через расход.






