Для элементарной струйки в потоке жидкости уравнение Бернулли имеет вид: 
, так как для потока: eк = av2/2g, где a» 1.1 - опытный коэффициент кинетической энергии, то: 
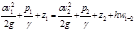- основное уравнение гидродинамики. Уравнение Бернулли устанавливает связь между скоростью движения, давлением и геометрическим расположением точек живого сечения потока.
28 вопрос Энергетический и геометрический смысл уравнения Бернулли для потока жидкости
Энергетический смысл: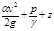 
- полная удельная энергия потока в живом сечении, так как 
- потенциальная удельная энергия давления, а z - потенциальная удельная энергия положения, то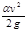 
- удельная кинетическая энергия, где v - средняя скорость в сечении; hw1-2 - затраты энергии на преодоление сил сопротивления.
Геометрический смысл: 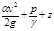- полный напор, так как - пьезометрический напор, а z - напор положения, то 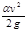- скоростной напор; hw1-2 - потерянный напор.
Пьезометрическая линия - ГМТ концов отрезков суммы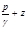 
. Пьезометрический уклон - изменение пьезометрической линии на единицу длинны. Напорная линия - ГМТ концов отрезков суммы 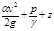. Гидравлический уклон - изменение напорной линии на единицу длинны
30 вопрос
Равномерным движением называют такое движение, параметры которого не изменяются ни во времени, ни в пространстве. Таким образом, равномерное движение всегда является установившимся.
При неравномерном движении параметры изменяются в пространстве. Неравномерное движение может быть как неустановившимся, так и установившимся. Неустановившееся движение всегда является неравномерным.
При напорном движении поток соприкасается со всеми точками периметра живого сечения и не имеет свободной поверхности.
При безнапорном движении поток движется со свободной поверхностью.
32- 27 вопрос
33 вопрос
. Совместное использование ур-ия Бернулли и гидравлического уравнения неразрывности
Уравнения могут быть использованы совместно при условии постоянного расхода
Q = ωύ = const. При установившемся движении несжимаемой жидкости произведение площади живого сечения на среднюю скорость потока является постоянной величиной.
ω1ύ1= ω2ύ2= ωύ = const, ύ1\ ύ2= ω2\ω1. Средние скорости потока обратно пропорциональны площадям соответствующих живых сечений.
Общая запись ур-ния Бернулли z1+p1\ρg+α1 ύ21\2g= z2+p2\ρg+α2 ύ22\2g+hw
Вопрос 34
гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (системгидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2]. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах учаска течения может быть и отрицательной (например, при эжекционном эффекте).
Гидравлические потери принято разделять на два вида:
потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;
местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Гидравлические потери выражают либо в потерях напора 
в линейных единицах столба среды, либо в единицах давления 
: 
, где 
— плотность среды, g —ускорение свободного падения.
Вопрос 35
режимы движения жидкости
Число Рейнольдса: Re=V*R/ν, где V – скорость, м/с; R - гидравлический радиус, м; v - кинематический коэффициент вязкости, м2/с. Re крит=2320.
Режим движения жидкости, при котором наблюдалось плавное, слоистое движение жидкости был назван ламинарным режимом движения жидкости (Re<2320). Режим движения жидкости сопровождавшийся хаотическим движением частиц жидкости в потоке был назван турбулентным (Re>2320).
Опыты показали, что переход от турбулентного режима к ламинарному происходит при определенной скорости (эта скорость называется критической), которая различна для разных жидкостей и диаметров труб; при этом критическая скорость растет с увеличением вязкости жидкости и с уменьшением диаметра труб.
Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока – число Рейнольдса Re=V*R/ν, где V – скорость, м/с; R - гидравлический радиус, м; v - кинематический коэффициент вязкости, м2/с.
Вопрос 36
потери напора по длине при турбулентном движении
Потери напора на трение по длине потока, возникающие при равномерном напорном движении жидкости в трубах, определяют по уравнению hдл=(λ*L*V^2)/(d*2g), где l – длина участка трубы, м; d – внутренний диаметр трубопровода, м; v – средняя скорость потока, м/с; g – ускорение свободного падения, м/с2; λ– безразмерный коэффициент гидравлического трения. Эта формула носит название формулы Дарси-Вейсбаха и является одной из основных формул гидродинамики.
Было установлено, что при больших числах Рейнольдса и высокой шероховатости коэффициент гидравлического трения λ в трубах совсем не зависит от вязкости жидкости (числа Рейнольдса), а зависит только от относительной шероховатости (в этих условиях трубы и русла называют вполне шероховатыми). Трубы же, в которых коэффициент λ зависит только от числа Рейнольдса и не зависит от относительной шероховатости, что бывает при сравнительно малых Re и k/d, называют гидравлически гладкими. При этом один и тот же трубопровод в одних условиях может быть гидравлически гладким, а в других – вполне шероховатым. Условия, в которых λ зависит и от числа Рейнольдса и от относительной шероховатости, называются переходной областью. Это объясняется тем, что при малых числах Рейнольдса вблизи стенок сохраняется сравнительно толстый ламинарный слой, и выступы шероховатости обтекаются жидкостью без образования и отрыва вихрей. Свойства поверхности стенок трубопровода в этом случае не влияют на сопротивление.
Коэффициент потерь напора по длине будет равен: ξ=λ*l/d
Коэффициент трения Дарси: λ=8*(U/V)^2
Вопрос 37
местные гидравлические сопротивления
Местные потери напора вызываются сопротивлениями в арматуре, фасонных частях и оборудовании, вследствие сужения и расширения потока, изменения направления движения жидкости, слияния и разделения потока и т. п.
Местные потери напора определяют как произведение скоростного напора непосредственно вблизи местного сопротивления ξ, по формуле hм=(ξ*V^2)/(2*g)
Коэффициенты местных сопротивлений, как правило, находят опытным путем.
Внезапное расширение потока. Этот случай поддается теоретическому обоснованию. Из опытов установлено, что поток жидкости, вытекающий из узкой трубы, не сразу заполняет все сечение широкой трубы; он отрывается от стенок и дальше двигается в виде расширяющейся струи. В кольцевом пространстве между струей и стенками трубы жидкость образует завихрения. На некотором расстоянии l от расширения трубопровода струя вновь заполняет все сечение. В результате вихревых движений жидкости между сечениями 1-1 и 2-2 идет постоянный обмен между струей и жидкостью в кольцевом пространстве. В результате этих явлений происходит переход механической энергии в тепловую, что и является причиной потерь напора. Диффузор.
формула Борда h вн.р.=(V1-V2)^2/2g
При внезапном сужении канала поток жидкости отрывается от стенок входного участка и лишь затем (в сечении 2 - 2) касается стенок канала меньшего размера. В этой области потока образуются две зоны интенсивного вихреобразования (как в широком участке трубы, так и в узком), в результате чего, как и в предыдущем случае, потери напора складываются из двух составляющих (потерь на трение и при сужении). Коэффициент потерь напора при гидравлическом сопротивлении внезапного сужения потока можно определить по эмпирической зависимости, предложенной Идельчиком: ξ=0,5*(1-ω2/ω1). Конфузор.
Вопрос 38
Русла подразделяют:
1) по параметрам, определяющим изменение площади живого сечения по длине потока:
(на непризматические и призматические (и цилиндрические ). У непризматических русел форма и (или) геометрические размеры поперечного профиля меняются по длине русла. Поэтому площадь живого сечения потока является функцией длины русла и функцией глубины потока вдоль русла. В таком русле движение неравномерное. В призматических руслах форма и размеры элементов поперечного профиля по длине сохраняются неизменными. Площадь живого сечения потока может изменяться только в связи с изменением глубины потока.
2) По форме профиля поперечного сечения: правильной и неправильной формы. Призматические русла имеют правильную форму. Они могут быть прямоугольные, треугольные, трапецеидальные. Если поперечный профиль русла правильной формы очерчен кривой линией, окружностью или параболой определяемой по всей длине русла одним уравнением, то такое русло называется цилиндрическим. Правильную форму чаще всего имеют искусственные русла. К руслам неправильной формы относятся полигональные (составные) русла (рис. и русла естественных потоков
3)Открытые русла в зависимости от продольного уклона дна делятся на русла с положительным (прямым) геометрическим уклоном i >0, когда дно русла понижается в направлении движения потока; горизонтальные русла при i = 0 и русла с отрицательным (обратным) уклоном дна i <0, когда дно русла повышается в направлении движения жидкости.
40 вопрос
гидравлические элементы потока
Живым сечением называется поверхность в пределах потока, проведенная перпендикулярно к линиям тока (элементарным струйкам). В общем случае эта поверхность криволинейная АВС. Однако в большинстве случаев практической гидравлики поток жидкости можно представить параллельно-струйным или с очень малым углом расхождения струек, а за живое сечение принять плоское поперечное сечение потока АС. Площадь живого сечения обозначается буквой s.
Смоченным периметром называется длина части периметра живого сечения, в пределах которой поток соприкасается с твердыми внешними стенками. Смоченный периметр обозначают буквой П.
Гидравлическим радиусом называется отношение площади живого сечения к смоченному периметру: R=S/П.
Примеры поперечных сечений потока: а) трапецеидальное; б) прямоугольное; в) круговое. Для кругового сечения, заполненного жидкостью полностью: S=п*d^2; П=п*d; R=S/П=d/4.
41 вопрос
Гидравлически наивыгоднейшим сечением канала является сечение, способное при заданной площади обеспечить максимальную пропускную способность.
Как известно из геометрии, наименьшим периметром (из всех возможных) обладает круг, и гидравлически наивыгоднейшим сечением для открытых каналов было бы сечение, имеющее форму полукруга. Далее при данной площади меньшими периметрами обладают правильные многоугольники, причем длина их периметра будет тем меньше, чем больше число сторон.
Следовательно, далее по выгодности идут различные сечения в форме половин правильных многоугольников, например половина шестиугольника, т. е. равнобочная трапеция с углом наклона боковых сторон б= 60°. Из прямоугольных профилей наивыгоднейшим является сечение в виде половины квадрата. Величина гидравлического радиуса для всех этих сечений равняется половине наибольшей глубины наполнения.
43 вопрос Формула Шези — формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока. Опубликована французским инженером-гидравликом А.Шези (Antoine de Chézy) (1718 – 1798) в 1769 году. Применяется для расчётов потоков в речных руслах и канализационых системах.
,
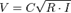де V — средняя скорость потока, м/с;
C — коэффициент сопротивления трения по длине (коэффициент Шези), являющийся интегральной характеристикой сил сопротивления;
R — гидравлический радиус, м;
I — гидравлический уклон м/м.
44 вопрос
Равномерным называется такое установившееся движение, при котором живые сечения вдоль потока не изменяются: в этом случае; средние скорости по длине потока также не изменяются, т.е.. Примером равномерного движения является: движение жидкости в цилиндрической трубе, в канале постоянного сечения при одинаковых глубинах.
Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и достоянными вдоль потока. Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.
Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).
Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное.
48 вопрос
ДАРСИ ФОРМУЛА
- формула, представляющая собой осн. закон ламинарной фильтрации: u = kl, где и - скорость фильтрации, k - коэф. фильтрации, характеризующий степень проницаемости рассматриваемого пористого тела, I - пьезометрический уклон.
Вопрос 53
истечения жидкости из отверстия и насадки при постоянном напоре
Напор истечения Ho=H+(p1-p2)/γ+α*ν^2/2g
Коэффициент скорости φ=1/√(α+ς)
Формула Торичелли ν=φ*√(2*g*Ho)
Для идеальной жидкости ς=0 и φ=1. Тогда ν=√(2*g*Ho)
Расход жидкости Q=φ*ε*ω*√(2*g*Ho), где ε=ωсж/ω – коэффициент сжатия струи.
Величину φ*ε обозначают через μ и называют коэффициентом расхода.
Таким образом, расход жидкости, вытекающей через отверстие, определяют по формуле Q=μ*ω*√(2*g*Ho)
Форма сечения струи жидкости при истечении претерпевает изменения.
Эти изменения называются инверсией. Инверсия происходит вследствие того, что скорости подхода к отверстию в разных точках его периметра различны и вследствие сил поверхностного натяжения.
При несовершенном сжатии коэффициент расхода μ1 вычисляют по формуле:
μ1=μ*(1+δ), где μ – значение коэффициента расхода при совершенном сжатии; δ – поправочный коэффициент, зависящие от отношения площади сечения отверстий ω к площади сечения сосуда ω1. Значения этих коэффициентов принимают по таблицам.
Насадкой называется отрезок трубы, длина которого в несколько раз больше внутреннего диаметра. Цилиндрические насадки встречаются в виде деталей гидравлических систем машин и сооружений. Конические сходящиеся и коноидальные насадки применяют для увеличения скорости и дальности полета струи воды (пожарные брандспойты, стволы гидромониторов, форсунки, сопла и др.).
Конические расходящиеся насадки применяют для уменьшения скорости и увеличения расхода жидкости и давления на выходе во всасывающих трубах турбин и др.
Скорость истечения V2=√(2*g*H)/√(1+ς),
Обозначая через коэф. скорости φн=1/√(α+ς): V2=φн*√(2*g*H),
Расход жидкости Q=φн*ω*√(2*g*Ho)
Насадки и коэф.:
Наружный цилиндрический ε=1, φ=0,82
Внутренний цилиндрический ε=1, φ=0,71
Конический сходящийся ε=0,98, φ=0,96
Конический расходящийся ε=1, φ=0,45
Коноидальный ε=1, φ=0,98
56 вопрос Насадки, скорость и расход при истечении жидкости через насадки при постоянном напоре
Насадки - присоединенные к отверстию патрубки длиной l<4d, позволяющие существенно изменять скорость и напор. Бывают:
1. внешние и внутренние;
2. призматические, цилиндрические, конические (сходящиеся и расходящиеся) и коноидальные.
Скорость и расход при истечении:
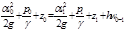, где 0-0 сечение - свободная поверхность жидкости, а 1-1 - сечение вблизи насадки. p0 = p1 = pатм, z0 - z1 = H.
, где zм - коэффициент местных потерь.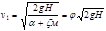 
, где j - коэффициент скорости. Расход: Q = w1 × v1 = e × wнасадки × v1, где e - коэффициент сжатия струи. 
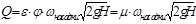, где m - коэффициент расхода жидкости.
Для внешней цилиндрической насадки:
| j | e | m |
| 0.82 | 1.00 | 0.82 |
Классификация насадок:
1. цилиндрические - на входе в насадку обрасуется вакуум, который подсасывает жидкость и увеличивает расход. Срыв вакуума происходит когда напор превышает атмосферное давление;
2. конические сходящиеся - уменьшение расхода, увеличение скорости;
3. конические расходящиеся - уменьшение скорости, увеличение расхода. Угол конусности ограничен, иначе истечение происходит как из отверстия в тонкой стенке;
4. коноидальные - увеличение расхода, увеличение скорости.
61вопрос
Истечение при переменном напоре при наличии постоянного притока
Истечение при переменном напоре при наличии постоянного притока Q0 (рис. 2.13).
Время t изменения напора от H1 до H2 в случае призматического резервуара (Ω = const) определяется формулой
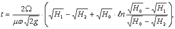
| 2.33 |
где H0 – напор при установившемся движении, когда расход из отверстия равняется притоку, т.е.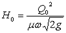 
Остальные обозначения упомянуты выше.
Формула (2.33) справедлива как для случаев повышения, так и для случая понижения горизонта в резервуаре, т.е. при Q0 > Q и Q0 < Q. Пределом изменения напора H в обоих случаях является H0.
63вопрос Истечение при переменном напоре при отсутствии притока
Истечение при переменном напоре при отсутствии притока (Q0 = 0 и, следовательно, H0 = 0).
В этом случае время t изменения напора от H1 до H2 определяется формулой
| 2.34 |
Отсюда вытекает, что время t наполнения или опорожнения резервуара при начальном напоре Н и конечном Н2 = 0 будет равно
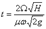
64 вопрос
Истечение при переменном напоре под переменный уровень
Если два резервуара соединены между собой, то при разных уровнях жидкости в этих резервуарах будет происходить переток жидкости из резервуара с более высоким положением уровня свободной поверхности в резервуар, где эта поверхность будет расположена на более низкой отметке.
Переток будет осуществляться при переменном (убывающем) расходе и продолжаться до тех пор, пока уровни жидкости в обоих резервуарах не сравняются.
Рассмотрим истечение при переменном напоре под переменный уровень (рис. 2.14).
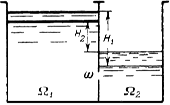
Рис. 2.14
Время t изменения напора от Н1 до Н2 при Ω1 = const и Ω2 = const определяется формулой
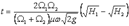
| 2.36 |
При одинаковых площадях резервуаров Ω1 = Ω2 из (2.36) получим:
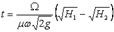
| 2.37 |
Для определения времени выравнивания горизонтов в смежных резервуарах (рис. 2.14) можно получить формулы, положив в (2.36) и (2.37) напор Н2 = 0.
Если аналитической связи между Ω и Н нет (например, в водохранилищах, перед плотинами), то уравнение (2.31) решается приближенными методами.
