Бесконечные абелевы группы

Введение

Определение 1. Алгебраической операцией на множестве M называется любое отображение f: M х M → M.

Таким образом, любой упорядоченной паре (m₁, m₂) элементов m₁, m₂ из множества M ставится в соответствие однозначно определённый элемент f((m₁,m₂)) того же множества M. При этом, образ пары f((m₁,m₂)) называется результатом алгебраической операции f.

На X может быть задано, вообще говоря, много разных операций.

Желая выделить одну из них, используют скобки: (X, *), и говорят,

что операция * определяет на X алгебраическую структуру или что

(X,*) — алгебраическая структура (алгебраическая система).

Определение 2. Бинарная операция * на множестве X называется ассоциативной, если (x * y) * z = x * (y * z) для всех x, y, z из множества M; она называется коммутативной, если x * y = y * x.

Определение 3. Элемент е X называется нейтральным (или единичным) относительно рассматриваемой бинарной операции *, если е * x = x * е = x

для всех х X. Если е' — ещё один единичный элемент, то, как следует из определения, е' = е' * е = е. Стало быть, в алгебраической структуре (X,*) может существовать не более одного нейтрального элемента.

Определение 4. Элемент x' X называется обратимым относительно рассматриваемой бинарной операции *, если x' * x = x * x' = e для всех х X. Если x” — ещё один обратный элемент к х, то, как следует из определения,

е= x'*x x” = е*х”= (x'*x)*x”=x'*(x*x”)=x'*e=x'. Стало быть, в алгебраической структуре (X,*) может существовать не более одного обратного элемента.

Определение 5.. Множество Х называется группой, если на нем задан групповой закон (произведение элементов), который каждой паре элементов x, y из множества Х сопоставляет третий элемент этого же множества, а также определена бинарная операция, удовлетворяющая следующим условиям:

 

1. Операция ассоциативна, т.е. для каждого x, y, z из множества Х

(x * y) * z = x * (y * z)

2. Существует нейтральный элемент e Х

3. Для любого элемента х Х существует обратный элемент х^-1 Х.

Группа Х называется абелевой (или коммутативной), если соответствующая алгебраическая операция коммутативна.

Группа Х называется конечной, если она состоит из конечного числа элементов, то есть | Х |< ∞.В противном случае группа называется бесконечной. Порядком конечной группы Х называется число элементов в ней | Х |.

 

Типы групп

Все группы условно можно разделить на типы в соответствии со схемой.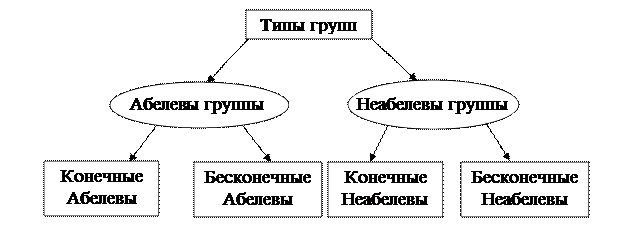

Конечные абелевы группы

Согласно определению конечной абелевой группы, можно выделить следующие примеры подобных групп.

 

Элементарные примеры:

I. Элементы е, а со законом композиции

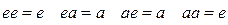
образуют абелеву группу.

II. Любое конечное кольцо – абелева группа относительно операции сложения.

III. Любое конечное поле без нуля – абелева группа относительно операции умножения.

IV.

 

Пример 1. Пусть (M, ∙) – группа и а ∈ M. Определим на М новую бинарную операцию * по правилу:

x * y = xay (x, y ∈ M)

Тогда (M, *) – абелева группа. В самом деле,

1) ассоциативность: (x * y) * z = (xay) * z = xayaz

x * (y * z) = x * (yaz) = xayaz

2) нейтральный элемент: a^-1

x * a^-1 =xaa^-1 = x

3) обратный элемент: x^-1

x * x^-1 =xax^-1 = a

4) коммутативность:

x * y = y * x = xay

Пример 2. Группа классов вычетов целых чисел по модулю n относительно операции сложения n – Z/nZ (циклическая группа порядка n), где n конечно

Зафиксируем натуральное число n и рассмотрим множество остатков от деления каждого натурального числа на n. Ясно, что различных остатков ровно n, они равны 0, 1, 2, …, n-1.

Разобьем множество Z на n классов по следующему принципу:

0) в нулевой класс соберем все такие числа, которые при делении на n дают остаток 0, т.е. целиком делятся на n;

1) в первый класс соберем числа которые при делении на n дают остаток 1;

…

n - 1) в (n - 1) класс соберем все такие числа, которые при делении на n дают остаток n-1

Теперь определим бинарную операцию ○ на множестве Z_n построенных классов. Пусть (k) и (m) – два класса. Выберем из них по числу: а = k (mod n),

b = m (mod n). Тогда a + b = k + m (mod n). Таким образом,

(k) ○ (m) =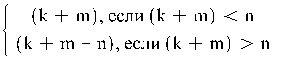

 

Множество Z_n относительно операции ○ образует группу, называемую группой вычетов по модулю n. Все групповые свойства выполнены: какие бы элементы группы мы не взяли, результат последовательного применения операции снова попадет в нашу группу, операция ○ ассоциативна, т.к. сводится к операции сложения чисел, нейтральным элементом служит нулевой класс (0), элементом, противоположным классу (k), является класс (n - k). Очевидно, что операция будет коммутативной.

Пример 3. Корни n -ой степени из единицы по умножению.

Возьмем в поле комплексных чисел совокупность корней n -ой степени из единицы.

Произведение двух корней n -ой степени из единицы само есть корень n -ой степени из единицы. Действительно, пусть ε ⁿ = 1 и η ⁿ = 1. Тогда

(εη) ⁿ= ε ⁿ η ⁿ = 1. Таким образом, произведение корней обладает групповым свойством. Докажем аксиомы группы.

1. Ассоциативность следует из того, что умножение комплексных чисел ассоциативно

2. Нейтральным элементом будет служить 1, которая, разумеется, принадлежит данному множеству.

3. Число, обратное корню n -ой степени из единицы, само есть такой же корень.

Действительно, если ε ⁿ = 1, то ε ε ^-1= 1, а значит, ε ⁿ (ε ^-1) ⁿ = 1, то есть

(ε ^-1) ⁿ = 1.

4. Коммутативность следует из коммутативности умножения комплексных чисел.

Таким образом, корни n -ой степени из единицы составляют по умножению абелеву группу, притом конечного порядка n.

Пример 4. Совокупность двоичных n-символьных комбинаций образует группу из 2ⁿ элементов, если в качестве групповой операции используется посимвольное сложение по модулю 2. Так, если а = (101110), b = (111011), то с = а + b = (010101). Нейтральным является элемент (000000), а обратным является сам элемент, так как 110010 + 110010 = 000000

 

Пример 5 Всевозможные повороты правильного треугольника вокруг его центра О.

Доказательство:

 

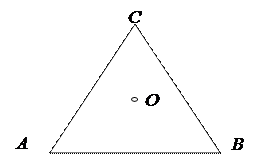
Два поворота считаются совпадающими, если они отличаются друг от друга на целое число полных оборотов (т.е. на кратное 360°). Несложно видеть, что среди всех поворотов треугольника лишь три поворота переводят треугольник в себя, а именно: повороты на 120°, 240° и нулевой поворот, оставляющий все вершины, а следовательно, и все стороны треугольника на месте. Первый поворот переводит вершину А в вершину В, вершину В в вершину С, вершину С в вершину А (он перемещает, как говорят, вершины А, В, С в циклическом порядке). Второй поворот перемещает А в С, В в А, С в В (т. е. перемещает в циклическом порядке А, С, В).

Пусть умножить два поворота —значит, последовательно произвести их один за другим.

Таким образом, поворот на 120°, умноженный с самим собой, дает поворот на 240°, умноженный с поворотом на 240° дает поворот на 360°, т. е. нулевой поворот. Два поворота на 240° дают поворот на 480° = 360° + 120°, т. е. их произведение есть поворот на 120°.

Если обозначить нулевой поворот через а₀, поворот на 120° через а₁ поворот на 240° через а₂, то получим следующие соотношения:

а₀ • а₀ = а₀, а₀ • а₁ = а₁ • а₀ = а₁,

а₀ • а₂ = а₂ • а₀ = а₂, а₁ • а₁ = а₂,

а₁ • а₂ = а₂ • а₁ = а₀, а₂ • а₂ = а₁.

Итак, для каждых двух поворотов определено их произведение. Это умножение удовлетворяет аксиоме ассоциативности. Действительно,

(а₀ • а₁) • а₂ = а₁ • а₂= а₀

а₀ • (а₁ • а₂) = а₀ • а₀ = а₀

 

Среди поворотов имеется также нулевой поворот а₀, который удовлетворяет условию

а • а₀ = а₀ • а = а

для любого поворота а.

Также каждый из трех поворотов имеет обратный ему поворот, дающий в произведении с данным поворотом нулевой поворот: нулевой поворот, очевидно, обратен самому себе, а₀^-1= а₀, так как а₀ • а₀ = а₀, тогда как а₁^-1 = a₂ и а₂^-1 = a₁ (так как a₁ • a₂ = а0).

Из определения следует, что умножение поворотов удовлетворяет коммутативности. Действительно,

а₀ • а₁ = а₁ • а₀ = а₁,

а₀ • а₂ = а₂ • а₀ = а₂,

а₁ • а₂ = а₂ • а₁ = а₀

Итак, умножение поворотов правильного треугольника, удовлетворяет всем перечисленным аксиомам абелевой группы.

 

Пример 6 Группа самосовмещений правильного n -угольника.

 

Доказательство:

Самосовмещением данной геометрической фигуры F назовем такое движенние плоскости или пространства, которое переводит F в себя, т. е. совмещает фигуру F с собой.

Пусть дан в плоскости правильный многоугольник .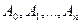

Требуется найти те движения плоскости, которые совмещают его с самим собой. При этом перемещении всякая вершина многоугольника должна перейти в вершину, всякая сторона - в сторону, а центр многоугольника – в себя, ибо он один.

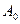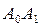Пусть при некотором перемещении вершина перейдет, положим, в . Тогда сторона должна перейти либо в сторону 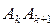либо в сторону 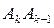. Но если бы сторона 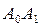перешла в сторону 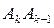, то треугольник 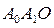перешел бы в треугольник .

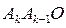Этот последний треугольник можно было бы, передвигая его в плоскости, перевести в положение , являющееся зеркальным отражением треугольника 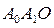относительно стороны 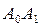. В результате оказалось бы, что мы треугольник 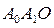перемещением в его плоскости перевели в его зеркальное отражение, а это невозможно.

Итак, сторона 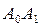должна перейти в сторону 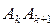. Точно таким же образом мы убеждаемся в том, что сторона переходит в , сторона переходит в и т. д. Другими словами, наше перемещение есть поворот многоугольника в его плоскости на угол

Введём операцию 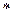композиции поворотов: , которая сводится к тому, что углы поворотов складываются.

Еще надо заметить, что два поворота, отличающиеся друг от друга на целое число полных углов , оказывают на наш многоугольник (как, впрочем, и на всю плоскость) одинаковое действие, и потому будут отнесены в один класс поворотов. Т.е., нас будет интересовать не величина угла поворота, а остаток от деления этого угла на 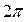. Классом поворотов назовем множество поворотов на углы вида , где .

Классы поворотов правильного n-угольника образуют группу по операции :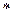
1. Нейтральным элементом является – класс поворотов на .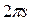
2. Обратным элементом для класса является класс поворотов .
3. Асооциативность очевидна, так как операция 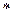определена через сложение чисел.
Остается заметить, что и в этой группе любой ее элемент может быть получен последовательным применением поворота на угол . Это означает, что группа вращений правильного n-угольника циклична.

 

Пример 6 Совокупность всех самосовмещений фигуры F с операцией произведения самосовмещений.

 

Доказательство:

Пусть в пространстве или на плоскости дана фигура F. Рассмотрим все самосовмещения этой фигуры, то есть все перемещения её (в пространстве или на плоскости), совмещающие эту фигуру с нею самой.

В качестве произведения 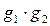двух самосовмещений и 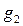определим перемещение, возникающее в результате последовательного совершения сначала перемещения 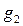, а потом перемещения . Очевидно, что перемещение 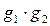также является совмещением фигуры F с собой, в предположении, что перемещения и 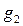порознь являются таковыми.
Совокупность всех самосовмещений фигуры F с только что определенной операцией произведения образует группу. В самом деле, умножение перемещений удовлетворяет условию ассоциативности; далее, в совокупности самосовмещений имеется единичное, или тождественное, самосовмещение (то есть перемещение, оставляющее каждую точку фигуры на месте). Наконец, к каждому самосовмещению g имеется обратное ему самосовмещение (передвигающее каждую точку назад, в исходное положение, из положения, которое оно заняло после перемещения g).

 

 

Пример 7 Группа поворотов правильной n-угольной пирамиды (вокруг ее оси).

 

Доказательство:

Очевидно, что группа поворотов правильной n-угольной пирамиды вокруг ее оси изоморфна группе поворотов правильного n-угольника, лежащего в ее основании; эта группа есть, таким образом, циклическая группа порядка n. Легко убедиться, что поворотами пирамиды вокруг оси
(на углы 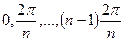) исчерпываются все перемещения, совмещающие пирамиду.

 

V. Группу самосовмещений тела, известного под названием «двойной правильной n-угольной пирамиды» или n-угольного диэдра.

Доказательство

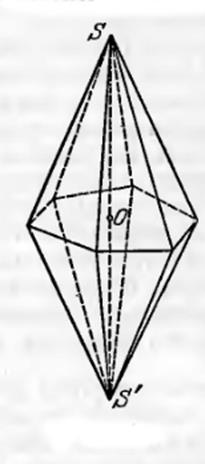
Это тело состоит из правильной n-угольной пирамиды и ее зеркального отражения в плоскости основания.

Докажем, что группа самосовмещений диэдра состоит из следующих элементов:
1) поворотов вокруг оси пирамиды (на углы );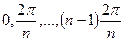
2) так называемых опрокидываний, т. е. поворотов на угол 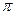вокруг каждой из осей симметрии «основания диэдра», т. е. правильного многоугольника, являющегося общим основанием обеих пирамид, составляющих диэдр. Таких осей симметрии имеется, как мы видели, n, так что перемещений второго рода имеется тоже п.
Число всех полученных перемещений есть, таким образом, 2 п. Чтобы убедиться в том, что (за исключением случая п = 4) не имеется никаких других перемещений, переводящих n-угольный диэдр в самого себя, заметим прежде всего, что в случае всякое совмещение диэдра с самим собой должно либо оставлять на месте точки S и S' (самосовмещения первого рода), либо менять их местами (самосовмещения второго рода). Далее, основание диэдра должно переходить при таком перемещении в самого себя. Заметим, наконец, что произведение (т. е. последовательное осуществление) двух самосовмещений первого рода дает самосовмещение первого рода, произведение самосовмещений первого рода с самосовмещениями второго рода дает самосовмещение второго рода, а произведение двух самосовмещений второго рода дает самосовмещение первого рода.
При этом произведение двух самосовмещений, из которых одно — первого, а другое — второго рода, зависит от порядка сомножителей: если а — самосовмещение первого, а b — самосовмещение второго рода, то .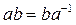
Рассмотрим сначала самосовмещения первого рода. При таких самосовмещениях основание переходит в само себя, оставаясь в своей плоскости; оно испытывает, таким образом, поворот на один из углов:

.

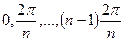Таким образом, и все перемещение диэдра оказы­вается поворотом вокруг оси диэдра на тот же угол.
Итак, самосовмещений первого рода имеется (вклю­чая тождественное самосовмещение, т. е. покой) ровно п. Эти самосовмещения суть не что иное, как повороты диэдра вокруг его оси на углы

.

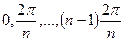Пусть дано некоторое вполне определенное самосовмещение второго рода, т. е. такое самосовмещение диэдра с самим собой, при котором вершины S и S' меняются местами.
Произведем после данного самосовмещения второго рода некоторое вполне определенное опрокидывание диэдра, т. е. перемещение, заключающееся в повороте диэдра на угол 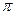вокруг одной какой-нибудь, раз навсегда выбранной, оси симметрии основания. Получим самосовмещение первого рода (так как этот поворот есть самосовмещение второго рода, а произведение двух самосовмещений второго рода есть самосовмещение первого рода), т. е. поворот диэдра вокруг его оси.

Итак, всякое самосовмещение второго рода переходит после одного и того же опрокидывания в некоторое самосовмещение первого рода. Отсюда следует легко: всякое самосовмещение второго рода можно получить, производя (до или после некоторого самосовмещения первого рода) одно и то же опрокидывание. Отсюда, далее следует,что число самосовмещений второго рода равно числу самосовмещений первого рода.т. е. п.
С другой стороны, ясно, что все опрокидывания являются самосовмещениями второго рода. Так как этих опрокидываний имеется ровно п, то ими, очевидно, и исчерпывается вся совокупность самосовмещений второго рода.
Итак, доказали следующее: группа самосовмещений п -угольного диэдра есть некоммутативная группа порядка 2 n, состоящая из п поворотов вокруг оси диэдра SS' и из п опрокидываний, т. е. поворотов на угол 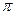вокруг осей симметрии основания диэдра. Все п опрокидываний получаются умножением одного из них на п поворотов диэдра вокруг его оси SS'.

Так как все повороты диэдра вокруг его оси получаются умножением с самим собой одного поворота — именно, поворота на угол — , то группа всех самосовмещений имеет систему образующих из двух элементов: поворота на угол и одного какого-нибудь опрокидывания.
Случай п = 4 является особым потому, что частным случаем четырехугольного диэдра является октаэдр, допускающий не 8, а как увидим ниже (в примере групп), 24 самосовмещения. Это объясняется тем, что при самосовмещении некоторых четырехугольных диэдров, а именно правильных октаэдров, вершина S может совмещаться не только с вершиной S', но и с каждой из вершин основания. Одно из необходимых для этого условий — одинаковое число граней (а также и ребер), примыкающих к каждой вершине, выполнено, очевидно, в случае любого четырехугольного диэдра. В случае правильного октаэдра и все углы, телесные и плоские, при любых двух вершинах оказываются соответственно равными так же, как и сами грани и ребра.

 

Бесконечные абелевы группы

Согласно определению бесконечной абелевой группы, можно выделить следующие примеры подобных групп.

 

Элементарные примеры:

I. Любое (бесконечное) кольцо – абелева группа относительно операции сложения.

II. Любое (бесконечное) поле без нуля – абелева группа относительно операции умножения (т. к. все его ненулевые элементы образуют коммутативную группу по умножению).

III. Группы, возникающие в числовых структурах относительно операции сложения – это, например: 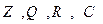. Это - абелевы бесконечные группы.

IV. Группы, возникающие в числовых структурах относительно операции умножения – это, например: . Это - абелевы бесконечные группы.

V.

 

 

Пример 1. Вращения на плоскости.

Пусть множество Ф – множество всех поворотов на угол φ.

При сложении двух углов φ₁ и φ₂ из Ф получаем угол φ₃ опять же из множества Ф φ₁+ φ₂= φ₃. Таким образом, операция вращения на плоскости обладает групповым свойством. Проверим аксиомы группы для данной операции.

1. Ассоциативность: (φ₁+ φ₂)+ φ₃= φ₁+ (φ₂+ φ₃)

2. Нейтральный элемент в этом случае – поворот на угол 0 (+ 2πn)

3. Обратным элементом является поворот на угол (– φ) (+2πn)

4. Коммутативность: φ₁+ φ₂ = φ₂+ φ₁

Итак, вращения вокруг оси, перпендикулярной выбранной плоскости, образуют абелеву группу.

 

Пример 2. Множество векторов трехмерного пространства

Действительно, для любых векторов а, b, с векторного пространства выполняется групповое свойство, так как при сложении двух векторов снова получается вектор. Аксиомы группы:

1. Ассоциативность: (a + b) + c = a + (b + c)

2. Нейтральный элемент: нулевой вектор 0 т.,ч. a + 0 = a

3. Обратный элемент: a + (- a) = 0

4. Коммутативность: a + b = b + a

 

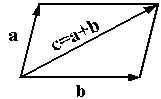
Таким образом, множество векторов трехмерного пространства образуют абелеву группу по сложению.

Пример 4. Кольцо является абелевой группой по сложению (из определения кольца), обратимые ненулевые элементы любого поля по умножению также составляет абелеву группу.

 

 

Конечные неабелевы группы

Конечная группа называется неабелевой, если не выполняется аксиома коммутативности. Рассмотрим следующие примеры конечных неабелевых групп.

Пример 1. Множество всех невырожденных матриц порядка n над полем Р с операцией умножения образует группу. Действительно, произведение двух невырожденных матриц будет невырожденным, единичная матрица является невырожденной, всякая невырожденная матрица обладает обратной матрицей, также невырожденной, закон ассоциативности, выполняясь для всех матриц, справедлив, в частности и для невырожденных.

 

Пример 2. Множество квадратных матриц порядка n, в каждой строке и каждом столбце которых ровно один ненулевой элемент, равный ± 1, относительно умножения.

В самом деле, умножение подобных матриц, снова дает матрицу из группы:

 

 

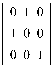
Проверим аксиомы группы:

1. Ассоциативность:

 

 

 

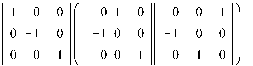
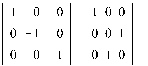
2. Нейтральный элемент: единичная матрица (принадлежит данной группе)

 

3. Обратный элемент: обратная матрица также будет принадлежать данной группе, так как определитель любой матрицы из группы равен ± 1, алгебраическое дополнение будет равно либо 0, либо 1.

 

4. Коммутативность не выполняется:

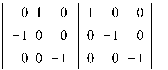
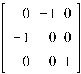
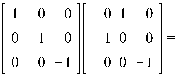
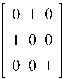
Пример 3. Совокупность четных подставок n- ой степени составляет по умножению группу, притом конечного порядка ½ n!

Четность подстановки совпадает с четностью числа транспозиций, входящих в разложение этой подстановки в произведение транспозиций. Поэтому произведение двух четных подстановок само четно: в самом деле, представление АВ в виде произведения транспозиций мы получим, записав соответствующие разложения для А и В одно за другим.

Путем проверки можно выяснить, что умножение будет ассоциативным. Четность тождественной подстановки очевидна. Наконец, четность подстановки А-1 при четной А следует хотя бы из того, что записи этих подстановок можно получить одну за другой переменой мест верхней и нижней строк, т.е. они содержат равное число инверсий.