Второй закон Кирхгофа
опубликовано: 23.08.2013.
СОДЕРЖАНИЕ:
- Падение напряжений в замкнутом контуре.
- Применение первого и второго законов Кирхгофа для расчета электрических цепей.
Падение напряжений в замкнутом контуре
При расчете электрических цепей нам часто приходится встречаться с цепями, которые образуют замкнутые контуры. В состав таких контуров, помимо сопротивлений, могут входить еще электродвижущие силы, то есть источники напряжений. На рисунке 1 представлен участок сложной электрической цепи. Задана полярность всех электродвижущих сил (э. д. с.). Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении, например по часовой стрелке. Рассмотрим участок АБ. На этом участке происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).

|
| Рисунок 1. Участок сложной электрической цепи |
На участке АБ:
φА + E 1 – I 1 × r 1 = φБ.
На участке БВ:
φБ – E 2 – I 2 × r 2 = φВ.
На участке ВГ:
φВ – I 3 × r 3 + E 3 = φГ.
На участке ГА:
φГ – I 4 × r 4 = φА.
Складывая почленно четыре приведенных уравнения, получим:
φА + E 1 – I 1 × r 1 + φБ – E 2 – I 2 × r 2 + φВ – I 3 × r 3 + E 3 + φГ – I 4 × r 4 = φБ + φВ + φГ + φА
или
E 1 – I 1 × r 1 – E 2 – I 2 × r 2 – I 3 × r 3 + E 3 – I 4 × r 4 = 0.
Перенеся произведения I × r в правую часть, получим:
E 1 – E 2 + E 3 = I 1 × r 1 + I 2 × r 2 + I 3 × r 3 + I 4 × r 4.
В общем виде

Это выражение представляет собой второй закон Кирхгофа. Формула второго закона Кирхгофа показывает, что во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжений. Бывают случаи, когда в замкнутом контуре отсутствуют источники э. д. с., тогда применимо другое определение второго закона Кирхгофа – алгебраическая сумма падений напряжений в замкнутом контуре равна нулю.
Видео 1. Второй закон Кирхгофа
Рассмотрим простой замкнутый контур (рисунок 2).

|
| Рисунок 2. Простой замкнутый контур |
По второму закону Кирхгофа

откуда
E = I × r 0 + I × r = I × (r 0 + r),
откуда

Мы получили формулу закона Ома для всей цепи.
Применение первого и второго законов Кирхгофа для расчета электрических цепей
|
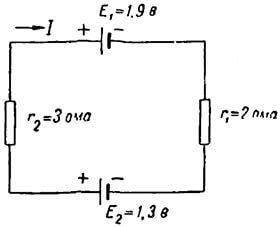
| Рисунок 3. Электрическая цепь – к примеру 1 |
Решим несколько задач, используя закон Ома и оба закона Кирхгофа.
Пример 1. Дана электрическая цепь (рисунок 3). Найти ее ток. Выберем произвольно положительное направление тока. Обходя контур по часовой стрелке, пишем уравнение второго закона Кирхгофа:
– E 1 + E 2 = I × r 1 + I × r 2; – 1,9 + 1,3 = I × (2 + 3); – 0,6 = 5 × I;
I = – 0,12
Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.
Пример 2. Дана электрическая цепь (рисунок 4). Определить токи на отдельных участках.
Произвольно выбираем положительные направления токов.

Рисунок 4. Электрическая цепь – к примеру 2
Для контура абде:
| 6 = 2 × I 1 + 5 × I 3. | (1) |
Для контура авге:
| 6 – 2 = 2 × I 1 – 4 × I 2; 2 = I 1 – 2 × I 2. | (2) |
Для точки Б по первому закону Кирхгофа:
| I 3 = I 1 + I 2. | (3) |
Имеем три уравнения с тремя неизвестными. Решая их, находим величину и направление токов. Подставляя значение тока I 3 из уравнения (3) в уравнение (1), получим:
6 = 2 × I 1 + 5 × I 1 + 5 × I 2;
Сложим уравнения для двух контуров почленно:
(6 = 7 × I 1 + 5 × I 2) + (2 = I 1 – 2 × I 2)
или
(12 = 14 × I 1 + 10 × I 2) + (10 = 5 × I 1 – 10 × I 2).
Сложив два последних уравнения, имеем:
22 = 19 × I 1, откуда I 1 = 1,156 А,
подставляем значение I 1 в уравнение (1):
6 = 2 × 1,156 + 5 × I 3,

Подставляем значение I 1 в уравнение (2):
2 = 1,156 – 2 × I 2,
откуда

Знак минус показывает, что действительное направление тока I 2 обратно принятому нами направлению.






