Билет
1. Электр энергиясының ерекшеліктері және қолдануы. Электр тізбектерінің құрамдас бөліктері.
Электр тлектр тзбегінің идеалды эл-рі: Идеалды элемент физ-қ құбылыстың моделі.Практикада идеалды эл-р болмайды.Белгілі бір жағдайда ж/е бер-ген дәлдікте идеалды элемент реалды элементті сипаттайды.Идеалды эл-т активті ж/е пассивті болып бөл/ді.
2. Периодты синусоидалы емес ток тізбегіндегі резонанс.
Билет
1. Топологиялық ұғымдар: түйін, тармақ, контур.
Түйін –электр тізбегінің кем дегенде үш тармағының түйіскен нүктесі.
Тармақ –элементтері өзара бірізді жалғанған, бойымен бір ғана ток жүретін тізбек бөлігі.
Контур деп бірнеше тармақ арқылы өтетін тізбектің тұйық бөлігін айтады
2. Периодты синусоидалы емес э.қ.к-тің., кернеудің және токтың максималды, әрекеттік және орташа мәндері туралы түсініктемелер және оларды есептеу
Синусоидалы емес шамалардың модульдарының орташа мәні деп бұл функцияның период ішіндегі модулінің орташа мәнін айтады:
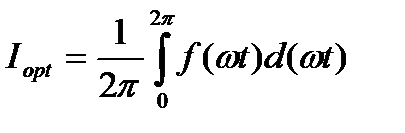 ,
, 
Токтың әрекеттік мәні:  .Мұндағы
.Мұндағы

Билет
1. Тұрақты ток көздері. Электр қозғаушы күш көзі (э.қ.к) және ток көзінің сипаттамалары.
Электр тізбегін талдау кезінде электр энергия көздерін мынадай есептік эквивалентпен (баламамен) айырбастайды: мәні реалды энергия көзінің ішкі кедергісіне тең және өзімен бірізді жалғанған кедергісі Ri бар электр қозғаушы күш көзімен (э.қ.к. көзі) немесе мәні реалды энергия көзінің ішкі кедергісіне тең және өзімен параллел жалғанған кедергісі Ri бар ток көзімен айырбастайды (1а және 1б сурет). Реалды э.қ.к. көзінің э.қ.к.-і Е болса, онда оның қысқыштарының арасындағы кернеу U=E-I∙Ri , яғни токқа тәуелді. Бұл U= f (I) тәуелдігін тізбектің сыртқы сипаттамасы деп атайды(1ә -сурет). Реалды э.қ.к. көзінің Ri мәні өте аз болатындықтан кернеудің азаю деңгейі тізбектегі токқа тікелей байланысты. Идеал э.қ.к. көзі үшін Ri =0, U=E, яғни оның қысқыштарының арасындағы кернеу әр уақытта тұрақты және ол арқылы жүретін токқа тәуелсіз
2. Периодты синусоидалы емес қисықтардың симметриялық шарттары туралы түсініктемелер. Фурье қатарындағы коэффиценттерді графикалық талдау әдісімен табу.
1)Абцисса өсіне симметриялы қисық сызықтар үшін  . Мұндай қисық сызықтардың өрнектеріде тұрақты мүше мен жұп гармоникалар болмайды: A0=A2=A4=A6=0;
. Мұндай қисық сызықтардың өрнектеріде тұрақты мүше мен жұп гармоникалар болмайды: A0=A2=A4=A6=0;  ;
;
2) Ордината осіне симметриялы қисық сызықтар үшін  . Бұл кезде синусоидалы гармоника болмайды:
. Бұл кезде синусоидалы гармоника болмайды:  ;
;  ;
;
3) Координата басына симметриялы қисық сызық үшін  . Өрнектерде тұрақты мүше және косинусоидалы гармоника болмайды, яғниА0=0,
. Өрнектерде тұрақты мүше және косинусоидалы гармоника болмайды, яғниА0=0,  ;
; 
Бұл тәсіл анықталған интегралды шекті санды қосылғыштар қосындысымен ауыстыруға негізделген. Егер f(ωt)- функциясы аналитикалық емес, графикалық түрде берілсе, онда А0 ,А′км және А″км- коэффициенттерін мына өрнектер бойынша анықтайды: 
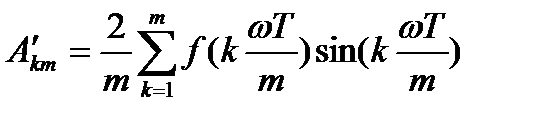 ;
; 
мұндағы т- периодтық синусоидалық емес функцияны бірдей кесінділерге бөлгендегі сан. Коэффициенттерді есептеу үшін Т-периоды т бірдей интервалға бөлінеді және сол т бөліну нүктелеріндегі қисықтың  -ординаталары анықталады, мұндағы к= 1,2,3... m.
-ординаталары анықталады, мұндағы к= 1,2,3... m.
4-билет
1. Тармақталмаған электр тізбегнің бөлігі үшін Ом заңы. Э.қ.к-і бар тармақталмаған электр тізбегі бөлігі үшін Ом заңы.
а) Тармақталмаған тізбекте э.қ.к. көзі болмаған жағдайда: I=U/R.
ә)Тармақталмаған тізбекте э.қ.к. көзі болған жағдайда: I=(U + E)/R. Өрнектегі «+» таңбасы Е мен I бағыттары бағыттас болғанда қойылады,ал «-» таңбасы Е мен I бағыттары қарама-қарсы болғанда қойылады.
2. Периодты синусоидалы емес э.қ.к., кернеу жєне ток. Олардың электр тізбегінде пайда болу себептері. Периодты синусоидалы емес шамаларды Фурье қатарына жіктеу.
5-билет
1. Толық тізбек үшін Ом заңын дәлелдеу.
б)Толық тізбек үшін Ом заңы: I=E/(Ri+Rж
2.Индуктивті байланысқан элементтері бар күрделі тізбекті есептеу кезіңдері
Мұндай тізбектерді есептеу үшін Кирхгоф екінші заңы бойынша теңдеулер құрған кезде, индуктивті орамалар үшін жазылатын кернеулердің өрнегіне өзара индукцияның комплекстік кернеуін  jωM I қосу керек. Егер орамалар үйлесімді қосылса, онда бұл комплекс оң таңбалы, ал қарсы қосылған жағдайда теріс таңбалы болады.
jωM I қосу керек. Егер орамалар үйлесімді қосылса, онда бұл комплекс оң таңбалы, ал қарсы қосылған жағдайда теріс таңбалы болады.
Индуктивті байланысқан элементтері бар тізбекті индуктивті байланысы жоқ балама сұлбамен ауыстыру арқылы тізбекті есептеуді жеңілдетуге болады. Екі элементтен (Z 1 және Z 2) тұратын индуктивті байланысы бар тізбекті балама сұлбамен ауыстырғанда Z 1 мен Z 2 кедергілеріне  Z м кедергісі жалғанады және олар мен жаңа пайда болған түйін арасына
Z м кедергісі жалғанады және олар мен жаңа пайда болған түйін арасына  Z м кедергісі қосылады. Егер индуктивті байланысқан үш элементтер үш сәулелі жұлдызша немесе ұшбұрыш арқылы жалғанған болса, онда жоғарыда келтірілген тәсіл бойынша индуктивті байланыстан құтылып, оған балама сұлбаға көшуге болады.
Z м кедергісі қосылады. Егер индуктивті байланысқан үш элементтер үш сәулелі жұлдызша немесе ұшбұрыш арқылы жалғанған болса, онда жоғарыда келтірілген тәсіл бойынша индуктивті байланыстан құтылып, оған балама сұлбаға көшуге болады.
Билет
1. Кирхгофтың бірінші және екінші заңдары. Кирхгофтың заңдары бойынша теңдеулер құру реті.
Кирхгоф бірінші заңы. Бірінші анықтамасы: Тізбектің кез-келген түйінінде түйіскен токтардың алгебралық қосындысы нөлге тең. Математикалық түрде жазылуы:  . Теңдеу құру үшін тұйінге кірген токтардың таңбасын «+», ал шыққан токтардың таңбасын «-» етіп алу керек.
. Теңдеу құру үшін тұйінге кірген токтардың таңбасын «+», ал шыққан токтардың таңбасын «-» етіп алу керек.
Екінші анықтамасы: Түйінге кірген токтардың арифметикалық қосындысы түйіннен шыққан тоқтардың арифметикалық қосындысына тең.
Кирхгоф екінші заңы. Бірінші анықтамасы: Тұйық контурдағы э.қ.к.-тердің алгебралық қосындысы сол контурдағы кедергілердегі кернеулердің түсулердің алгебралық қосындысына тең. Екінші анықтамасы: Кез-келген тұйық контурдың бойындағы кернеулердің алгебралық қосындысына нөлге тең.
Математикалық түрде жазылуы:  ,
, 
Кирхофтың екінші заңы бойынша теңдеу құрудың реті:
а) Тізбектің тармақтарындағы токтардың бағыттарын өз қалауымызша таңдап аламыз;
ә) Тізбектің контурларын айналу бағытын өз қарауымызша таңдап аламыз;
б) Э.қ.к.- тің алгебралық қосындысын тапқан кезде контурдағы э.қ.к.-нің бағыты контурды айналу бағытымен сәйкес келсе, онда оның таңбасы «+», ал керісінше жағдайда «-» болады;
в) Токтың бағыты контурды айналу бағытымен сәйкес келсе, онда кернеудің түсуінің таңбасы таңбасы «+», ал керісінше жағдайда «-» болады.
Бірінші заң бойынша құрылатын теңдеулер саны: т- 1, мұндағы т- тізбектегі түйіндер саны.
Екінші заң бойынша құрылатын теңдеулер саны: к - (т- 1 ), мұндағы к- тізбектегі тармақтар саны.
2. Темір өзексіз трансформатор құрылысы және сипаттамалары.
Трансформатор - деп тізбектегі энергияны басқа тізбекке электромагниттік индукция құбылысы арқылы беретін аппаратты айтады. Оның қарапайым түрі ферромагниттік өзекшесіз индуктивті байланысқан екі орамадан тұрады. Кернеу көзі бірінші орамаға қосылады, ал жүктеме екінші орамаға қосылған. Трансформатордың теңдеулері мына түрде жазылады:

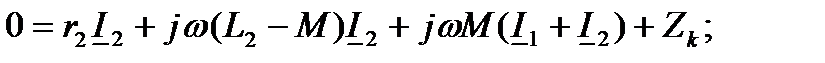
Мұндағы r1, L1 және r2 , L2 – бірінші және екінші орамалардың активті кедергілері және индуктивтері; Z қ = rқ +jXқ –жүктеменің кедергісі; I 1, I 2 – бірінші және екінші орамадағы токтар. Екінші орамадағы ток: I2 =-jXm I 1 /(r2қ +jX2қ). Токты трансформациялау коэффициенті: ki=I2 /I1 =Xm /z2қ. Кернеуді трансформациялау коэффициенті: ku = U2 / U1. Егер L1 < M<L2 болса,онда L1 - M теріс, яғни сиымдылық сипатта болады. Бұл жағдайда U2 > U1, демек, трансформатор кернеуді жоғарлатады. Егер L1 > M > L2 болса,онда L2 - M теріс, яғни сиымдылық сипатта болады. Бұл жағдайда U2 <U1, демек, трансформатор кернеуді төмендетеді.
Билет
1. Идеал сыйымдылық элементі бар тізбектің сипттамалары.
Егер сыйымдылық элементке синусоидалы кернеу u = Umsin  t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді:
t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді:
 18-сурет
18-сурет
 19-сурет
19-сурет
| q=Cu= СUmsin  t. Сыйымдылық элементпен жүретін ток i = dq/dt = C t. Сыйымдылық элементпен жүретін ток i = dq/dt = C 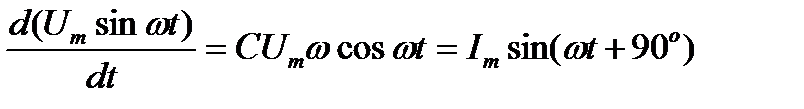 . Бұдан Im= UmC . Бұдан Im= UmC  = =  = Um/xc , мұндағы xC= = Um/xc , мұндағы xC=  сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc.
Фазалық ығысу сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc.
Фазалық ығысу  = =  u - u -  i =0-90o= -90o, яғни векторлық диаграммада сыйымдылық элементпен жүретін токтың I векторы кернеудің U векторынан фаза бойынша 90о-қа озады (19-сурет).
Лездік қуат: p = i u = Imsin( i =0-90o= -90o, яғни векторлық диаграммада сыйымдылық элементпен жүретін токтың I векторы кернеудің U векторынан фаза бойынша 90о-қа озады (19-сурет).
Лездік қуат: p = i u = Imsin( t+90o)Umsin t+90o)Umsin  t = (sin2 t = (sin2  t) t)  , яғни ол екі еселенген жиілікпен өзгереді Оның амплитудасын реактивті сыйымдылық қуат Qс деп атайды.
QC= , яғни ол екі еселенген жиілікпен өзгереді Оның амплитудасын реактивті сыйымдылық қуат Qс деп атайды.
QC=  ; Өлшем бірлігі- [ВАр] ; Өлшем бірлігі- [ВАр]
|
2.Тізбектегі индуктивті байланысы бар элементтерді параллель жалғау сұлбасы. Мұндай тізбектің сипаттамалары және векторлық даиграммалары.
Өзара индуктивтігі М, кедергілері r1 мен r2, ал индуктивтері L1 мен L2 болатын екі қабылдағыш параллель қосылған.
 37-сурет
37-сурет
| Орамалардың аттас ұштары бір түйінге қосылған (37 -сурет). Токтар мен кернеулердің таңдап алынған оң бағытында I = I 1 + I 2; U = Z 1 I 1+ Z m I 2; U = Z m I 1+ Z 2 I 2,,мұндағы Z 1=r1+ jωL1,, Z 2=r 2+ jωL2,, Z m=jωM. Бұл теңдеулерді шешкенде  ; ;  ; ;  ; ;
|
Бұдан тізбектің комплекстік кедергісі  .
.
Тізбектің толық индуктивтігі Lүйл  . Тармақтар арасында индуктивтік байланыс болмаған жағдайда, яғни Z m=0 болғанда, бұл өрнек мына түрге келеді:
. Тармақтар арасында индуктивтік байланыс болмаған жағдайда, яғни Z m=0 болғанда, бұл өрнек мына түрге келеді:  .
.
Егер орамалардың аттас ұштары әр түйінге қосылған болса, яғни орамалар қарсы қосылған жағдайда, кернеудің теңдеуіндегі Z m таңбасы минусқа өзгереді. Демек, бұл жағдайда тізбектің кірістік комплекстік кедергісі  , ал толық индуктивтілігі Lқар
, ал толық индуктивтілігі Lқар 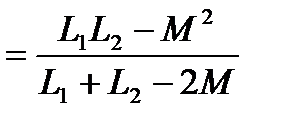 .
.
Векторлық диаграмма деп жиіліктері бірдей синусоидалық шамаларды комплекстік жазықтықта олардың бастапқы фазаларына сәйкес өзара орналасқан векторларының жиынтығын айтады. Фазалық ығысу деп синусоидалық шамалардың бастапқы фазаларының айырмасын айтады:  =φ2 - φ1.
=φ2 - φ1.
Билет
1. Қуаттар тепе-теңдігін дәлелде.
Тізбектегі қоректендіргіштердің қуаттарының алгебралық қосындысы сол тізбектегі тұтынушылардың қуаттарының арифметикалық қосындысына тең. Қоректендіргіштің қуаты
Рқ =E∙I, ал тұтынушы қуаты Pт =I2 ∙R формулалары арқылы анықталады.
2. Индуктивті байланысы бар элементтер тізбектеп жалғанған күйінің теңдеуі, сипаттамалары және векторлық даиграммалары.
Тізбек бірізді қосылған r1 мен r2 активті кедергілерден және L1 мен L2 индуктивтіліктен құралсын. Индуктивті элементтер арасындағы магниттік байланысты өзара индуктивтілік М сипаттайды. Оларды тізбекке қосудың екі сұлбасы болуы мүмкін. Индуктивтілік орамаларды үйлесімді қосқан кезде олардың аттас ұштарымен салыстырғанда тізбектегі ток бір бағытта жүреді. Сондықтан әр индуктивті элементпен ілінісетін өзіндік индукцияның және өзара индукцияның магнит ағындары қосылады. 36а–суретте көрсетілген тізбек үшін Кирхгоф екінші заңы бойынша теңдеу құрайық. Егер токтар бағыттары орамалардың аттас ұштарына байланысты бірдей болмаса, онда орамалар өзара қарсы қосылған. Бұл жағдайда бірінші ораманың толық ағын ілінісуі Ψ1 = Ψ11 - Ψ12, ал екінші ораманың толық ағын ілінісуі Ψ2 = Ψ22 - Ψ21. Ir 1+ L 1 di/dt + M di/dt+L 2 di/dt+ M di/dt+ir 2 = e. Комплекстік түрде: I[ r 1+ r 2+ jω(L1+L2+2M)]= E.
Бұдан орамалар үйлесімді қосылған кездегі олардың толық индуктивтілігін анықтаймыз: Lүйл =L1+L2+2M. Тізбектің толық кедергісі Z үйл= r 1+ r 2+ jω(L1+L2+2M)= Z 1+ Z 2+2 Z m, мұндағы Z 1=r1+ jωL1, Z 2= r 2+ jωL2,, Z m= jωM.- орамалардың комплекстік кедергілері және өзара индукцияның комплекстік кедергісі.
Орамалар үйлесімді қосылған жағдайға сәйкес келетін векторлық диаграма 36ә–суретте көрсетілген.
Билет
1. Бір э.қ.к-і бар электр тізбектерін есептеу. Балама түрлендіру тәсілі
Бір қоректендіргіші бар электр тізбектерін есептеу үшін балама түрлендіруді қолдануға болады.
а) Кедергілері бірізді жалғанған электр тізбегін есептеу үшін кедергілерді бір балама (эквивалент) кедергімен Rб айырбастаймыз (2-сурет). Бұл жағдайда тізбектегі ток I= U/Rб. Балама кедергінің Rб мәнін анықтау үшін Кирхгофтың екінші заңы бойынша теңдеу құрамыз: U=U1+U2+U3, мұндағы U1=I∙R1 ; U2=I∙R2; U3=I∙R3; U = I∙Rб. Сонда I∙Rб=I∙R1+ I∙R2+ I∙R3 = I(R1+R2+R3). Бұл теңдеуден Rб=R1+R2+R3. Егер кедергілер бірізді жалғанса, онда балама кедергінің мәні осы кедергілердің арифметикалық қосындысына тең.
2. Тізбектегі өзара индуктивтік. өзаралық индукциясыныњ э.қ.к.-і.
Тізбектің бір контурында немесе бір элементінде ток өзгерген кезде басқа контурда немесе басқа элементте э.қ.к. пайда болса, онда осы екі контурды немесе екі элементті бір-бірімен индуктивті байланысқан (магнитті байланысқан) дейді, ал екінші контурда немесе екінші элементте пайда болған э.қ.к.-ті өзаралық индукцияның э.қ.к.-і деп атайды.
Өзара қатар ораласқан, орам сандардары w1 және w2 тең екі индуктивтілік орамалармен i 1 және i 2 токтары жүрсе, онда әр ораманың барлық магнит сызықтары екінші ораманың орамдарымен ілінісуі мүмкін, яғни Ф21 =Ф11, Ф12 =Ф22. Сондықтан мұндай тізбектерді талдау кезінде орамалардың өздерінің ағын ілінісулерінен (Ψ11 және Ψ22) басқа қосымша ағын ілінісулерін (Ψ12 және Ψ21) есепке алу керек. Бірінші ораманың өзіндік ағын ілінісуі Ψ11=Ф11 w1= L1 i 1, бірінші ораманың тогының әсерінен пайда болған екінші орамадағы қосымша ағын ілінісуі Ψ21= Ф21 w2 =Ф11 w2=М21 i 1, мұндағы М21= Ψ21/ i 1 –пропорциональдық коэффициент, өзаралық индуктивтілік деп аталады. Бұл өрнектерден
L1/ М21= w1/ w2.
Екінші ораманың өзіндік ағын ілінісуі Ψ22=Ф22 w2= L2 i 2, екінші ораманың тогының әсерінен пайда болған бірінші орамадағы қосымша ағын ілінісуі Ψ12= Ф12 w1 =Ф22 w1=М12 i 2. Бұл өрнектерден L2/ М12= w2/ w1. Көрсетілген екі қатынастан М12 М21= L1L2 екендігін көруге болады. Тәжірибе М12 = М21=М екендігін көрсетеді. Демек, өзаралықиндуктивтілік М=  .
.
Билет
1.Кедергілердің бірізді, параллель және аралас жалғануы
Кедергілері бірізді жалғанған электр тізбегін есептеу үшін кедергілерді бір балама (эквивалент) кедергімен Rб айырбастаймыз (2-сурет). Бұл жағдайда тізбектегі ток I= U/Rб. Балама кедергінің Rб мәнін анықтау үшін Кирхгофтың екінші заңы бойынша теңдеу құрамыз: U=U1+U2+U3, мұндағы U1=I∙R1 ; U2=I∙R2; U3=I∙R3; U = I∙Rб. Сонда I∙Rб=I∙R1+ I∙R2+ I∙R3 = I(R1+R2+R3). Бұл теңдеуден Rб=R1+R2+R3. Егер кедергілер бірізді жалғанса, онда балама кедергінің мәні осы кедергілердің арифметикалық қосындысына тең,
Кедергілері параллель жалғанған электр тізбегін есептеу үшін кедергілерді бір балама (эквивалент) кедергімен Rб айырбастаймыз. Бұл жағдайда тізбектегі толық ток I= U/Rб. Балама кедергінің Rб мәнін анықтау үшін Кирхгофтың бірінші заңы бойынша теңдеу құрамыз. Параллель тармақтар саны үшеу болған жағдайда I=I1+I2+I3, мұндағы I1=U/R1 , I2=U/R2 , I3=U/R3 – параллель тармақтардағы токтар. Сонда U/Rб=U/R1+U/R2+U/R3. Бұл теңдеуден 1/Rб=1/R1+1/R2+1/R3немесе Gб=G1+G2+G3, мұндағы Gб ,G1 ,G2 ,G3 –тізбектің толық өткізгіштігі және параллель тармақтардың өткізгіштіктері. Жалпы жағдайда 1/Rб=1/ +1/R2+1/R3+...+1/ Rn , Gб=G1+G2+G3+…+ Gn.
б) Кедергілері аралас жалғанған электр тізбегін есептеу үшін алдымен параллель тармақтардың кедергісін бір балама кедергімен R23 айырбастаймыз: 1/R23=1/R2+1/R3. Сонан кейін R1 мен R23 бірізді жалғанғандықтан балама кедергімен Rб= R1+ R23 айырбастаймыз (3-сурет). Тізбектегі толық ток
I1=U/Rб=U/(R1+R23).I2 мен I3 токтарын табу үшін Uаб кернеуін табамыз: Uаб=I1 ∙R23. Бұдан кейін токтарды табуға болады: I2=Uаб/R2, I3=Uаб/R3.
2.Тербелмелі контурлардың жиіліктік сипаттамалары.
Билет
1. Кедергілердің жұлдызша және үшбұрышша жалғануы.
Түрлендіру кезінде мынандай шарттар орындалуы керек:а)Үшбұрыштың А,В,С түйіндеріндегі потенциалдар жұлдызшаның А,В,С потенциалына тең болуы керек; ә)Үшбұрыштың А,В,С түйіндеріне келетін токтар жұлдызшаның осы түйіндерге келетін токтарына тең болуы керек; б)Түрлендіру тізбектің басқа бөлігіне әсер етпеуі керек.
Жұлдызша сұлбаның кедергілерін түрлендірілген үшбұрыш сұлбаның кедергілері арқылы табуға болады: RA=RAB ∙RCA /(RAB+RCA+RBC); RB=RAB ∙RBC /(RAB+RCA+RBC); RC=RCA∙RBC /(RAB+RCA+RBC).
Жұлдызша сұлбаны үшбұрыш сұлбаға түрлендіргенде оның кедергілері төмендегі формулалар арқылы табылады: RAB=RA+RB+RA∙RB/RC; RBC=RB+RC+RB∙RC/RA; RCA=RC+RA+RC∙RA/RB
2Токтар резонансының болу шарты және сипаты.
 Токтар резонансы тізбекте мынадай шарттар бір мезгілде пайда болғанда болады: а) r, L, C элементтері параллель жалғануы керек (24-сурет); ә)сыйымдылық өткізгіштік bL индуктивті өткізгіштікке bC тең болуы керек, яғни bL=bC.
Токтар резонансы тізбекте мынадай шарттар бір мезгілде пайда болғанда болады: а) r, L, C элементтері параллель жалғануы керек (24-сурет); ә)сыйымдылық өткізгіштік bL индуктивті өткізгіштікке bC тең болуы керек, яғни bL=bC.
Билет
1.Э.қ.к-тердің бірізді және параллель жалғануы. Балама генератордың параметрлері.
Бұл тәсіл күрделі тізбектің бір тармағындағы токты табу үшін қолданылады. Бұл тәсіл бойынша есептеу үшін қарастырылатын тармақты тізбектің басқа бөлігінен бөліктеп аламыз. Қалған бөлікті активті екіұштық деп қарастырамыз. Активті екіұштық дегеніміз екі ғана жалғану ұшы бар, ал ішінде э.қ.к. мен резисторлар бар тізбекті айтамыз
2.Синусоидалы ток тізбегіндегі резонанстық режимдер. Кернеулер резонансының сипаты
резонанстық режимі деп осы екіұштықтың кірістік кедергісі тек активті сипатта болып, реактивті кедергі немесе реактивті өткізгіштік нөлге тең болған жағдайды айтамыз. Басқаша айтқанда, сыртқы тізбекке қатысты екіұштық өзін резонанстық режимде активті кедергі секілді сезінеді. Сондықтан соның кірісіндегі кернеу және токтың фазалары бір-біріне сәйкес келеді. Ал екіұштықтың бұл кездегі реактивті қуаты нөлге тең болады. Резонанстық режимді екі түрге бөледі: кернеулер резонансы және токтар резонансы
Электр тізбегінде кернеулер резонансы болу үшін мынадай екі шарт бір мезгілде орындалуы қажет: 1) r, L, C - элементтері тізбектей жалғануы керек; 2) индуктивті кедергі xL сыйымдылық кедергіге xC тең болу керек.
Билет
1.Электр тізбегінің негізгі принциптері
1)Беттестіру принципі: Егер тізбекте бірнеше электр қозғаушы күштер болса, онда осы тізбектің кез келген тармағындағы ток осы электр қозғаушы күштердің сол тармақта әрқайсы тудырған токтарының алгебралық қосындысына тең.
2)Теңгеру принципі: Тізбектің тармағындағы кедергіні сандық мәні сол кедергі мен токтың көбейтіндісіне тең, ал бағыты токтың бағытына қарама- қарсы электр қозғаушы күшімен айырбастауға болады.
3)Өзаралық принцип: Тізбектің k тармағына орналасқан э.қ.к. m тармағында Im (Im=Eк ∙Gkm) тогын тудырса, онда m тармағындағы э.қ.к. Еm=Eк k тармағында мәні Im-ге тең Ik (Iк =Em ∙Gmk)тогын тудырады. Gkm, Gmk -өзаралық өткізгіштіктер.
2.Айнымалы токтың топографиялық диаграммалары.
Топографиялық диаграммада оның белгілі бір нүктесіне тізбек сұлбасының белгілі бір нүктесінің комплекстік потенциалы сәйкес келеді. Потенциалы нөлге тең деп алынған сұлба нүктесі координаталар басына тура келеді. Топографиялық диаграмма тізбектің кез-келген нүктелерінің арасындағы кернеуді оңай анықтауға мүмкіндік береді. Ол үшін диаграммадағы тиісті нүктелерді түзумен қосады.
Билет
1.Бірнеше э.қ.к-тері бар күрделі тұрақты ток тізбектерін есептеу әдістері.
Тұрақты токтың күрделі тізбектерін есептеу үшін мынандай тәсілдерді қолдануға болады:
1) Кирхгофтың заңдарын пайдаланып есептеу тәсілі; 2) Контурлық токтар тәсілі; 3) Түйіндік потенциалдар тәсілі; 4) Екі түйіндік тәсіл; 5) Балама генератор тәсілі.
2.Синусоидалы ток тізбегі үшін қуаттар тепе- теңдігі
Синусоидалы ток тізбегіндегі қуаттар тепе-теңдігі мынаны білдіреді: біріншіден, тізбектегі барлық қоректендіргіштердің активті қуаттарының алгебралық қосындысы сол тізбектегі резистивті элементтердің активті қуаттарының арифметикалық қуаттарының қосындысына тең:
∑UқорIқор cos(φu – φi)= ∑rIr 2 немесе ∑Pқор = ∑Pr
Билет
1.Ом заңын пайдалану арқылы есептеу.
2.Комплекстік түрде жазылған Ом жєне Кирхгоф заңдары.
Билет
1.Контурлық токтар әдісіі
Бұл тәсілді қолданған кезде электр сұлбасының тәуелсіз контурында тек өзінің контурлық тогы жүреді деп есептейді. Контурлық токдеп қарастырылған контурдың барлық тармақтарымен жүреді деп шартты түрде қабылданған ток. Бұл тәсіл бойынша теңдеулер Кирхгофтың екінші заңы бойынша контурлық токтарға байланысты құрылады
Әрбір контур үшін контурлық токтың бағытын өз қалауымызша, мысалы сағат тілінің жүрісінің бағытымен бағыттас етіп таңдап аламыз. Екі контурға ортақ тармақпен жүретін контурлық токтар бағыттас болса, онда олардың қосындысы алынады. Керісінше жағдайда олардың айырмасын алады
2. Тізбегінің комплекстік қуатын анықтау.
Билет
.1.Түйіндік потенциалдар әдісі
Сұлбалардағы түйіндердің потенциалдарын белгісіз ретінде қабылдап, электр тізбектерін есептеу тәсілін түйіндік потенциалдар тәсілі деп атайды.Айталық, сұлбада n-түйін болсын. Сұлбаның кез-келген бір нүктесін ойша жермен қосамыз, яғни оның потенциалын нөлге тең деп аламыз.Соның нәтижесінде белгісіздер саны n-1-ге дейін азаяды. Бұл тәсіл бойынша теңдеулер Кирхгофтың бірінші заңы бойынша түйінде түйіскен токтарға арнап құрылады. Токтарды түйіндердің потенциалдары арқылы Ом заңы бойынша өрнектеуге болады
2.Кедергілер, кернеулер және қуаттар үшбұрыштары арқылы тізбекті сипаттау.
Билет
1. Екі түйіндік әдіс.
Көп жағдайда екі түйіннен тұратын электр сұлбалар кездеседі. Мұндай сұлбаларды есептеу үшін түйіндік потенциалдар тәсілінің жеке бір түрі –екі түйіндік тәсілді қолданған тиімді. Бұл тәсіл бойынша екі түйін арасындағы кернеуді табу арқылы тармақтардағы токтарды анықтайды.
18-билет
2.Синусоидалы ток тізбегін комплекстік өткізгіші
Комплекстік өткізгіштік деп комплекстік кедергіге кері шаманы айтады:
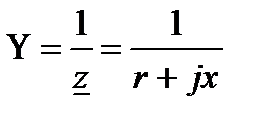 ,
, 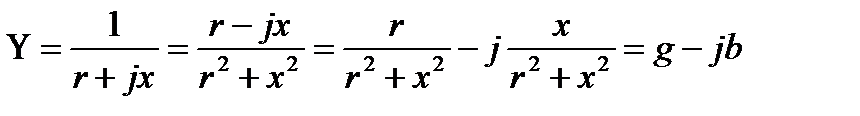
 , мұндағы
, мұндағы  ,
,  - активті өткізгіштік,
- активті өткізгіштік, 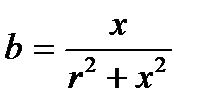 - реактивті өткізгіштік,
- реактивті өткізгіштік,  - толық өткізгіштік.
- толық өткізгіштік.
Ом заңын комплекстік өткізгіштік арқылы жазайық: I = U Y, I = U g – U b= I a + I p.
Сонымен электр тізбегінің толық өткізгіштігі нақты бөлігі активті өткізгіштікке, ал жорамал бөлігі реактивті өткізгіштікке тең комплекс сан ретінде жазылады.
Билет
1. Активті екіполюстық. Балама генератор әдісі.
Активті екіұштық – тізбектің басқа бөлігімен екі ұштық арқылы жалғанатын, ал құрамына резисторлар мен энергия көздері кіретін тізбектің бөлектенген тармағы.
Бұл тәсіл күрделі тізбектің бір тармағындағы токты табу үшін қолданылады. Бұл тәсіл бойынша есептеу үшін қарастырылатын тармақты тізбектің басқа бөлігінен бөліктеп аламыз. Қалған бөлікті активті екіұштық деп қарастырамыз. Активті екіұштық дегеніміз екі ғана жалғану ұшы бар, ал ішінде э.қ.к. мен резисторлар бар тізбекті айтамыз. Егер екіұштықтың ішінде энергия көзі (қоректендіргіш) болмаса, онда оны пассивты екіұштық дейді және оны электр энергиясын қабылдаушы деп санайды. Балама сұлбада пассивты екіұштықты бір кедергімен бейнелейді. Ол кедергіні екіұштықтың ішкі немесе кірістік кедергісі деп атайды.
2.Синусоидалы ток тізбегін комплекстік кедергісі
 Комплекстік тәсіл лездік мәндер үшін құрылатын дифференциалдық теңдеуден комплекстік мәндер үшін құрылатын алгебралық теңдеуге өткізуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде синусоидалық шамаларды комплекстік сандар ретінде көрсетеді:
Комплекстік тәсіл лездік мәндер үшін құрылатын дифференциалдық теңдеуден комплекстік мәндер үшін құрылатын алгебралық теңдеуге өткізуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде синусоидалық шамаларды комплекстік сандар ретінде көрсетеді:
1. А  , мұндағы
, мұндағы 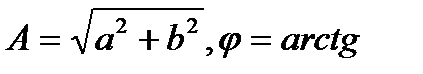 b/a.
b/a.
2. Егер  , онда
, онда  . Егер
. Егер  , онда
, онда 
Кез-келген векторды  -ға көбейткенде, ол вектордың модулін өзгертпей 90о-қа бұрады.,ал -
-ға көбейткенде, ол вектордың модулін өзгертпей 90о-қа бұрады.,ал -  -ға көбейткенде векторды - 90о-қа бұрады (28-сурет). Комплекстік тәсілді пайдалану арқылы синусоидалы шамалардың лездік мәндерін анықтайтын дифференциалдық теңдеулерден комплекстік мәндер арқылы өрнектелген алгебралық теңдеулерге көшуге болады. Бұл есептеу жұмысын жеңілдетуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде токтың лездік мәнін (i) оның комплекстік амплитудалық мәніне (I m) айырбастаймыз, ал лездік активті кернеуді ua=ir комплекстік активті кернеумен. I m r, лездік индуктивті кернеуді uL=L di/dt комплекстік индуктивті кернеумен I m jωL, ал лездік сыйымдылық кернеуді uC=(1/C) ∫idt комплекстік сыйымдылық кернеумен I m(-j/ωC), лездік э.қ.к.-ті e комплекстік кернеумен E m айырбастаймыз.
-ға көбейткенде векторды - 90о-қа бұрады (28-сурет). Комплекстік тәсілді пайдалану арқылы синусоидалы шамалардың лездік мәндерін анықтайтын дифференциалдық теңдеулерден комплекстік мәндер арқылы өрнектелген алгебралық теңдеулерге көшуге болады. Бұл есептеу жұмысын жеңілдетуге мүмкіндік береді. Комплекстік тәсілді пайдаланған кезде токтың лездік мәнін (i) оның комплекстік амплитудалық мәніне (I m) айырбастаймыз, ал лездік активті кернеуді ua=ir комплекстік активті кернеумен. I m r, лездік индуктивті кернеуді uL=L di/dt комплекстік индуктивті кернеумен I m jωL, ал лездік сыйымдылық кернеуді uC=(1/C) ∫idt комплекстік сыйымдылық кернеумен I m(-j/ωC), лездік э.қ.к.-ті e комплекстік кернеумен E m айырбастаймыз.
Билет
1.Активті екіполюстықтың қабылдағышқа максимал қуат беру шарты.
Активті екіұштыққа қосылған жүктемеде Rж бөлінетін қуат P = I2 R = U аб бж Rж /(Rж+ Ri). Қабылдағышқа максимал қуат беру шартын анықтау үшін P-ның Rж бойынша бірінші ретті туындысын тауып,оны нөлге теңейміз. Осыдан Rж = Ri. Демек осы теңдік орындалған жағдайда жүктемеде максимал қуат бөлінеді: Pmax= U2 аб бж /4Rі. Балама генераторда бөлінетін толық қуат Pтол =U аб бж I =U2 аб бж /(Rж+ Ri). Пайдалы әсер коэффициенті (п.ә.к.): η= P/ Pтол = Rж /(Rж+ Ri). Егер Rж = Ri болса, онда η=0,5.
2.Активті кедергі, идеал индуктивті элемент жєне сыйымдылық элементтер тізбектеп жалғанған тізбектің сипаттамалары
Бірізді жалғанған r, L және C элементтерден тұратын электр тізбегі арқылы (20-сурет) синусоидалы ток i=Imsin  t жүргенде, осы тізбектегі кернеулердің лездік мәндері үшін Кирхгофтың екінші заңы бойынша теңдеу құруға болады: u= ur+uL+uC. Онда тізбек күйінің теңдеуі:
t жүргенде, осы тізбектегі кернеулердің лездік мәндері үшін Кирхгофтың екінші заңы бойынша теңдеу құруға болады: u= ur+uL+uC. Онда тізбек күйінің теңдеуі:
 201-сурет 201-сурет
| u= ri+ L  + +  = rImsin = rImsin  t+Im t+Im  Lcos Lcos  t - t -  немесе
u=rImsin немесе
u=rImsin  t+Im t+Im  Lsin( Lsin( t+90o)+ t+90o)+ 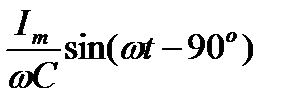 =Umrsin =Umrsin  t+UmLsin( t+UmLsin( t++90o) +Umcsin( t++90o) +Umcsin( t - 90o).
Уақытқа тәуелді үш синусоидалы функцияның қосындысын комплекстік тәсілмен есептеген тиімді. Лездік кернеу мен ток негізінде комплекстік ток пен кернеуді жазайық: I t - 90o).
Уақытқа тәуелді үш синусоидалы функцияның қосындысын комплекстік тәсілмен есептеген тиімді. Лездік кернеу мен ток негізінде комплекстік ток пен кернеуді жазайық: I 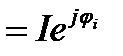 ,
21билет ,
21билет
|
1. Электр схемасын түрлендіру әдістері.
2. Активті кедергі, идеал индуктивті элемент жєне сыйымдылық элементтер параллель жалғанған тізбектің сипаттамалары.
 Параллель қосылған активті кедергі r, идеал индуктивті элемент L және сыйымдылық элементтен C тұратын электр тізбегін синусоидалы кернеуге u=Umsinωt қосайық(25-сурет). Барлық тармақтардағы токтарды анықтайық. Кирхгофтың бірінші заңы бойынша:
Параллель қосылған активті кедергі r, идеал индуктивті элемент L және сыйымдылық элементтен C тұратын электр тізбегін синусоидалы кернеуге u=Umsinωt қосайық(25-сурет). Барлық тармақтардағы токтарды анықтайық. Кирхгофтың бірінші заңы бойынша: 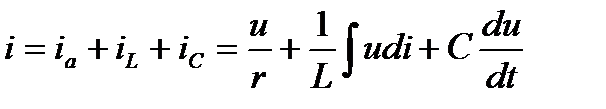 ,немесе i =(Um/r)sinωt+(Um/ωL) sin(ωt-90˚)+ωCUm sin(ωt+90˚).
,немесе i =(Um/r)sinωt+(Um/ωL) sin(ωt-90˚)+ωCUm sin(ωt+90˚).
Билет
1. Контурлық токтар әдісін дәлелде
2. Активті кедергі, идеал сыйымдылық элементтер бар тізбектің сипаттамалары
Активті кедергісі бар тізбек. Кедергісі бар элементті резистор дейді. Осы резистордың айнымалы токқа көрсететін кедергісін активті кедергі деп атайды. Активті кедергі айнымалы токтың электр энергиясының жылу энергиясына айналуын сипаттайды. Егер сыйымдылық элементке синусоидалы кернеу u = Umsin  t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді: q=Cu= СUmsin
t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді: q=Cu= СUmsin  t. Сыйымдылық элементпен жүретін ток i = dq/dt = C
t. Сыйымдылық элементпен жүретін ток i = dq/dt = C 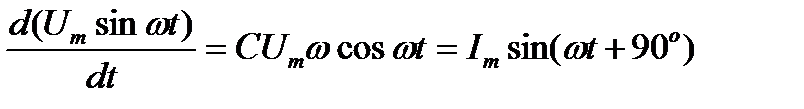 . Бұдан Im= UmC
. Бұдан Im= UmC  =
=  = Um/xc , мұндағы xC=
= Um/xc , мұндағы xC=  сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc.
сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc.
Билет
1. Түйіндер әдісін дәлелде
2. Активті кедергі, идеал индуктивті элементі бартізбектің сипаттамалары
Активті кедергісі бар тізбек. Кедергісі бар элементті резистор дейді. Осы резистордың айнымалы токқа көрсететін к0едергісін активті кедергі деп атайды. Активті кедергі айнымалы токтың электр энергиясының жылу энергиясына айналуын сипаттайды
Синусоидалы кернеуді u=Umsin( t+
t+  u)активті кедергісі бар тізбекке берсек (13а-сурет), онда кедергі арқылы жүретін токтың лездік мәні
u)активті кедергісі бар тізбекке берсек (13а-сурет), онда кедергі арқылы жүретін токтың лездік мәні
i=u/r= Um/r sin( t+
t+  u)=Imsin(
u)=Imsin( t+
t+  i). Бұдан токтың әрекеттік мәні
i). Бұдан токтың әрекеттік мәні
I= (Um/  ) /r, ал фазасы
) /r, ал фазасы  i=
i=  u, Фазалық ығысу
u, Фазалық ығысу  =
=  u-
u-  i = 0
i = 0
Сонымен токтың I және кернеудің комплекстердің U векторлары өзара бір түзудің бойында орналасады және бағыттас болады (13б-сурет). Лездік қуат деп кернеудің лездік мәнінің токтың лездік мәніне көбейтіндісін айтады: р=ui = UmImsin2  t = UmIm(
t = UmIm( )=
)= 
Идеал индуктивті элементі бар тізбек (15-сурет ). Индуктивтік элемент уақытқа байланысты магнит ағынының өзгерісінен э.қ.к.-тің туу құбылысын және нақты электр тізбегінің элементінде магнит өрісінің
Билет
1. Беттестіру әдісі
Егер тізбекте бірнеше электр қозғаушы күштер болса, онда осы тізбектің кез келген тармағындағы ток осы электр қозғаушы күштердің сол тармақта әрқайсы тудырған токтарының алгебралық қосындысына тең.
2. Идеал сыйымдылық элементі бар тізбектің сипттамалары.
Егер сыйымдылық элементке синусоидалы кернеу u = Umsin  t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді, q=Cu= СUmsin
t берілген болса, ондағы заряд та синусоидалы заңдылықпен өзгереді, q=Cu= СUmsin  t. Сыйымдылық элементпен жүретін ток i = dq/dt = C
t. Сыйымдылық элементпен жүретін ток i = dq/dt = C 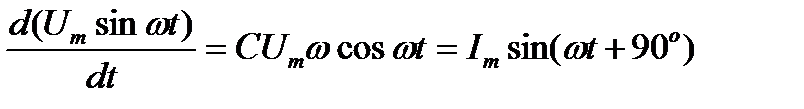 . Бұдан Im= UmC
. Бұдан Im= UmC  =
=  = Um/xc, мұндағы xC=
= Um/xc, мұндағы xC=  сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc.
сыйымдылық кедергі. Токтың әрекеттік мәні I= Uc/xc.
Билет
1. Потенциалдық диаграмма нені сипаттайды
Потенциалдық диаграмма потенциалдың тізбектің өн бойындағы өзгерісін сипаттайды. Тізбектің бір нүктесінің потенциалын нөлге тең деп алады да, қалған нүктелердің потенциалдарын осы нүктенің потенциалымен салыстыра отырып анықтайды. Абцисса осіне масштаб бойынша кедергілерді салады, ал ордината осінде потенциалдарды көрсетеді.
2. Идеал индуктивті элементі бар тізбектің сипаттамалары
Индуктивтік элемент уақытқа байланысты магнит ағынының өзгерісінен э.қ.к.-тің туу құбылысын және нақты электр тізбегінің элементінде магнит өрісінің энергиясының жинақталу құбылысын есептеуге мүмкіндік береді. Индуктивті орамамен айнымалы ток жүрген кезде оның бойында бағыты сол токқа қарама- қарсы өзіндік э.қ.к. eL пайда болады.

Билет
1.Кирхгоф заңдарын пайдалану арқылы есептеу
Кирхофтың заңдарын пайдалану арқылы есептеу тізбектің тармақтарындағы анықталуға тиісті токтарға қатысты теңдеулер құрудан басталады. Құрылатын теңдеулер саны белгісіз токтар санына тең. Кирхгофтың бірінші заңы бойынша құрылатын теңдеулер саны тізбектегі түйін санынан біреуге кем болады, яғни т- 1 тең.Мұндағы т- тізбектегі түйіндер саны. Кирхгофтың екінші заңы бойынша құрылатын теңдеулер саны жалпы құрылатын теңдеулер саны мен бірінші заңы бойынша құрылатын теңдеулер санының айырмасына тең, яғни к -(т- 1 ). Мұндағы к- тізбектегі тармақтар саны. Кирхгофтың екінші заңы бойынша теңдеулер құру кезінде басқа контурға кірмеген тармағы бар тәуелсіз контурлар үшін құруға тырысқан жөн.
2.Активті кедергі барайналмалы тізбектің сипаттамалары.
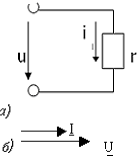
Кедергісі бар элементті резистор дейді. Осы резистордың айнымалы токқа көрсететін кедергісін активті кедергі деп атайды. Активті кедергі айнымалы токтың электр энергиясының жылу энергиясына айналуын сипаттайды.
 13-сурет
13-сурет
| Синусоидалы кернеуді u=Umsin( t+ t+  u)активті кедергісі бар тізбекке берсек (13а-сурет), онда кедергі арқылы жүретін токтың лездік мәні
i=u/r= Um/r sin( u)активті кедергісі бар тізбекке берсек (13а-сурет), онда кедергі арқылы жүретін токтың лездік мәні
i=u/r= Um/r sin( t+ t+  u)=Imsin( u)=Imsin( t+ t+  i). Бұдан токтың әрекеттік мәні
I= (Um/ i). Бұдан токтың әрекеттік мәні
I= (Um/  ) /r, ал фазасы ) /r, ал фазасы  i= i=  u, Фазалық ығысу u, Фазалық ығысу  = =  u- u-  i = 0
Сонымен токтың I және кернеудің комплекстердің U векторлары өзара бір түзудің бойында орналасады және бағыттас болады (13б-сурет). Лездік қуат деп кернеудің лездік мәнінің токтың лездік мәніне көбейтіндісін айтады: р=ui = UmImsin2 i = 0
Сонымен токтың I және кернеудің комплекстердің U векторлары өзара бір түзудің бойында орналасады және бағыттас болады (13б-сурет). Лездік қуат деп кернеудің лездік мәнінің токтың лездік мәніне көбейтіндісін айтады: р=ui = UmImsin2  t = UmIm( t = UmIm( )= )= 
|
Илет
1. Кирхгоф заңдарының матрицалық түрі
2. Айналмалы вектор және комплекстік сандар арқылы бейнелеу жолдары.
Айнымалы вектор арқылы бейнелеу. Тікбұрыштық координаталар жазығында ұзындығы синусоидалы токтың i=Imsin( t+
t+  ) амплитудасына Im тең вектор
) амплитудасына Im тең вектор  тең бұрыштық жылдамдықпен айналып тұр делік (11-сурет). Бастапқы жағдайда вектор абцисса осінен
тең бұрыштық жылдамдықпен айналып тұр делік (11-сурет). Бастапқы жағдайда вектор абцисса осінен  бұрышына ығысқан. Уақыт өткен сайын вектор
бұрышына ығысқан. Уақыт өткен сайын вектор  t жылдамдығымен айналып, шеңбер сызып шығады Егер вектордың әрбір сәттегі ордината осіндегі проекциясыларын уақыттық диаграмма түрінде бейнелесек, онда проекцияның синусоидалы заңдылықпен өзгеретіндігін көреміз, яғни вектордың ордината осіндегі проекциясының уақытқа тәуелді өзгерісі синусоидалы шаманың лездік мәндерін өзгерісін сипаттайды. Демек, синусоидалы шаманы ұзындығы оның амплитудасына тең, жылдамдығы оның бұрыштық жиілігіне тең айналмалы вектор түрінде бейнелеуге болады. Вектордың бастапқы жағдайы синусоидалы шаманың бастапқы фазасымен
t жылдамдығымен айналып, шеңбер сызып шығады Егер вектордың әрбір сәттегі ордината осіндегі проекциясыларын уақыттық диаграмма түрінде бейнелесек, онда проекцияның синусоидалы заңдылықпен өзгеретіндігін көреміз, яғни вектордың ордината осіндегі проекциясының уақытқа тәуелді өзгерісі синусоидалы шаманың лездік мәндерін өзгерісін сипаттайды. Демек, синусоидалы шаманы ұзындығы оның амплитудасына тең, жылдамдығы оның бұрыштық жиілігіне тең айналмалы вектор түрінде бейнелеуге болады. Вектордың бастапқы жағдайы синусоидалы шаманың бастапқы фазасымен  анықталады. Бұрыштық жиілігі бірдей бірнеше синусоидалы шамалардың векторлары бірдей жылдамдықпен айналады. Сондықтан олардың өзара орналасуы өзгермейді
анықталады. Бұрыштық жиілігі бірдей бірнеше синусоидалы шамалардың векторлары бірдей жылдамдықпен айналады. Сондықтан олардың өзара орналасуы өзгермейді
Синусоидалық шамаларды комплекс сандар арқылы бейнелеу. Синусоидалы шама тригонометиялық функция түрінде берілсін: i=Imsin( t + φ). Комплекстік жазықтыққа ұзындығы амплитудаға Im тең, ал нақты осьпен құрайтын бұрышы бастапқы фазаға φ тең вектор саламыз (12- сурет). Бұл вектордың ұшы белгілі бір комплекс санға - синусоидалы шаманың комплекстік амплитудасына сәйкес келеді. Im = Imej
t + φ). Комплекстік жазықтыққа ұзындығы амплитудаға Im тең, ал нақты осьпен құрайтын бұрышы бастапқы фазаға φ тең вектор саламыз (12- сурет). Бұл вектордың ұшы белгілі бір комплекс санға - синусоидалы шаманың комплекстік амплитудасына сәйкес келеді. Im = Imej  - комплекстік амплитуда.Уақыт өткен сайын фаза өседі де, бұл вектор айналмалы векторға айналады: Imej(
- комплекстік амплитуда.Уақыт өткен сайын фаза өседі де, бұл вектор айналмалы векторға айналады: Imej(  t+
t+  )= Imcos(
)= Imcos( t+
t+




